Если у тебя депрессия, поговори с бомжом и дай ему кусок хлеба. Твоя депрессия развеется, как утренний туман! © Александр Дьяков 1025 - | 919 - или читать все...
Обратная связь Пожаловаться на материал

Интерполяционные формулы Ньютона для равноотстоящих узлов


⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

 

В силу единственности многочлена степени n, построенного по n+1 узловым значениям функции f(х), формула Ньютона является разновидностью записи интерполяционного многочлена. Однако данная формула удобнее в случае, когда вычисления производятся для сеточных функций с разным количеством узлов. При этом добавление нового узла интерполирования приводит лишь к добавлению одного слагаемого интерполяционного многочлена. В то время как по формуле Лагранжа приходится делать пересчет всей таблицы.

В начале таблицы используют первую интерполяционную формулу Ньютона, а в конце – вторую. Рассмотрим один из способов построения первой интерполяционной формулы.

Пусть некоторая функция f(х) задана табличными значениями у0=f(х0); у1=f(х1);...; уn=f(хn) в равноотстоящих узлах интерполяции {х0, х1=х0+h;...; хn=x0+n×h}. Требуется построить интерполяционный полином Ньютона Ln(х) степени n, при котором

Ln(х0) º у0; Ln(х1) º у1; ...; Ln(хn) º уn .

Будем искать полином в виде

Ln(x0) = a0+ a1(x–x0) +a2(x–x0)×(x–x1) + ...+ an(x–x0) ×(x–x1) ×...× (x–xn)

где аi –неизвестные коэффициенты.

Для того чтобы найти а0, положим х=х0. Очевидно, что при этом Ln(х0) ºу0. Но так как все члены уравнения, кроме  первого, содержат сомножитель (x - x0), следовательно, они все станут равными нулю,   т.е. а0 º у0 .

Для того чтобы найти а1, положим х=х1. Повторив все рассуждения и учитывая, что значение полинома в указанной точке будет тождественно равно у1, после подстановки в формулу х1 имеем

Ln(x1) = a0+ a1× (x1 – x0) = у0 + а1 ×h = у1 .

Все остальные сомножители при неизвестных коэффициентах аi будут равны нулю. Преобразуя последнее выражение, находим а1  как а1 = D1/h, где D1 = Ln(х0 + h) –Ln(х0) = у1 – у0 .

Для того чтобы определить а2, положим х=х2 и, рассуждая аналогично, определим третий коэффициент как a2= D2 /(2! h2).

Подставляя в выражение последовательно все хn, приходим к общей формуле для получения коэффициентов аi:

 ai =Di /( i!×hi).

Тогда интерполяционный многочлен Ньютона для равноотстоящих узлов будит выглядеть :

 

Сделав в данной формуле замену переменных: t=(х-х0)/h, где h – шаг интерполирования получаем первую интерполяционную формулу Ньютона:

                                (15)

Вторую интерполяционную формулу Ньютона получают, если узлы интерполяции в Ln(х) берут в несколько ином порядке:

Ln(x0) = a0+a1×(x–xn)+a2(x–xn) ×(x–xn-1)+...+an× (x–xn) ×(x–xn-1)×...×(x–x0).

Тогда, рассуждая, как и в случае первой интерполяционной формулы, получаем искомую форму записи полинома Ньютона, которая известна как вторая интерполяционная формула:

Выполнив подстановку t=(х - хn)/h, получим иную запись интерполяционного многочлена Ньютона:

 (16)

П р и м е р. Реализовать в Microsoft Excel и MathCad первую и вторую интерполяционные формулы для функции, заданной таблицей равноотстоящих узлов

x 0 1 2 3 4
y -1,6 -2,305 -3,678 -10,96 -5,356

Построить графики интерполируемой и интерполирующих функций, совместив их на одной координатной плоскости.

 

Решение

a) Реализация задачи в Microsoft Excel показана на рис. 8.

 

б) Решение задачи в MathCad показана на рис. 9.

На практике при определении промежуточных значений функции, заданной таблично, не всегда целесообразно привлекать в вычислительный процесс все конечные разности. Можно заметить, что довольно хороший результат может быть получен при использовании уже конечных разностей выше третьего порядка. При этом первую интерполяционную формулу Ньютона целесообразно использовать для интерполирования в начале заданной таблицы, а при интерполировании в конце таблицы – вторую интерполяционную формулу.

П р и м е р. В MathCad протабулировать функцию на отрезке [0; 4], разбив его равномерной сеткой на 10 элементарных отрезков. Для полученной таблицы реализовать интерполяционную формулу Ньютона используя четыре конечные разности.

                             .

 

                                        Решение

 

Решение задачи в MathCad показана на рис. 10.

З а м е ч а н и е. Если интерполируемая функция сама является многочленом n-ной степени, то конечные разности n-го порядка будут постоянными, а конечная разность (n+1)-го порядка равна 0.

1.2.5. Интерполяционные формулы с центральными разностями

При построении интерполяционных формул Ньютона используются лишь значения функции, лежащие по одну сторону от выбранного начального значения, т. е. эти формулы носят односторонний характер.

Во многих случаях оказываются полезными интерполяционные формулы, содержащие как последующие, так и предшествующие значения функции по отношению к её начальному значению. Наиболее употребительными из них являются те, которые содержат разности, расположенные в горизонтальной строке диагональной таблицы разностей данной функции, соответствующей начальным значениям x0 и y0, или в строках, непосредственно примыкающих к ней. Эти разности Dy-1, Dy0, D2y-1,… называются центральными разностями (таблица 1), где xi=x0+i×h (i=0, ±1, ±2,…), yi=f(xi), Dyi=yi+1–yi, D2yi=Dyi+1–Dyi и т. д.

Таблица

x y Dy D2y D3y D4y D5y D6y D7y D8y
x-4 y-4 Dy-4              
x-3 y-3 Dy-3 D2y-4 D3y-4          
x-2 y-2 Dy-2 D2y-3 D3y-3 D4y-4 D5y-4      
x-1 y-1 Dy-1 D2y-2 D3y-2 D4y-3 D5y-3 D6y-4 D7y-4  
x-0 y0 Dy0 D2y-1 D3y-1 D4y-2 D5y-2 D6y-3 D7y-3 D8y-4
x1 y1 Dy1 D2y0 D3y0 D4y-1 D5y-1 D6y-2    
x2 y2 Dy2 D2y1 D3y1 D4y0        
x3 y3 Dy3 D2y2            
x4 y4                

 

Соответствующие интерполяционные формулы носят название интерполяционных формул с центральными разностями. К их числу относятся формулы Гаусса, Стирлинга и Бесселя.

Существуют определённые рекомендации по применению этих формул. Так формулу Гаусса и Бесселя целесообразно применять в случае когда 0,25£çtç£0,75, а формулу Стирлинга, если çt ç£0,25, где .

Интерполяционные формулы Гаусса. Пусть имеется 2n+1 равноотстоящих узлов интерполирования: x –n, x –(n–1),…, x –1, x0, x1, …, xn-1, xn и для искомой функции y=f(x) известны её значения в этих узлах yi=f(xi) (i=0, ±1, ±2,…).

Требуется подобрать многочлен L2n(x) степени не выше 2n такой, что L2n(xi)=yi.

Будем искать этот многочлен в виде

L2n(x)=a0+a1×(x–x0)+a2×(x–x0)×(x–x1)+ a3×(x–x–1)×(x–x0)×(x–x1)+…+a2n-1× × (x–x –(n-1)) ×…×x0×…×(x–x(n-1))+a2n×(x–x–n) ×…×x0×…×(x–xn),

где .

Введя переменную  и понятие обобщённых степеней t[m]=t(t-1)(t-2)…(t-(m-1)) получим первую интерполяционную формулу Гаусса:

                        (17)

Первая интерполяционная формула Гаусса содержит центральные разности

, , ,  , , , …

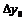Аналогично можно получить вторую интерполяционную формулу Гаусса, содержащую центральные разности

Вторая интерполяционная формула Гаусса имеет вид

                                  (18)

П р и м е р. Подобрать интерполяционный полином Гаусса для функции, заданной таблицей

x 0,2 0,25 0,3 0,35 0,4 0,45 0,5
y 1,552 1,67188 1,783 1,88463 1,976 2,05638 2,125

Найти значение интерполяционного многочлена в точке х=0,31.

 

Решение

 

Составляем таблицу конечных разностей, приняв x0=0,35, y0=1,8847 (табл.)

 

x y Dy D2y D3y D4y
0,2 1,552 0,119875      
0,25 1,67188 0,111125 -0,00875 -0,00075  
0,3 1,783 0,101625 -0,0095 -0,00075  
0,35 1,88463 0,091375 -0,01025 -0,00075  
0,4 1,976 0,080375 -0,011 -0,00075  
0,45 2,05638 0,068625 -0,01175    
0,5 2,125        

 

Так как разности третьего порядка практически постоянны, то в формуле Гаусса можно ограничиться конечными разностями третьего порядка. На основании этого можно сделать предположение, что исходная функция является многочленом третьей степени.

Применяя первую интерполяционную формулу Гаусса, будем иметь интерполяционный многочлен

Для рассматриваемого примера определим .

Подставив в данную формулу значение переменной t= – 0,8 получим L(x)=1,804109.

Интерполяционная формула Стирлинга. Взяв среднее арифметическое первой и второй интерполяционных формул Гаусса (17) и (18), получим формулу Стирлинга

…+ + +

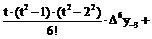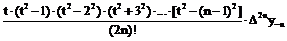+ (19)

П р и м е р. Решить предыдущую задачу с помощью интерполяционной формулы Стирлинга.

Решение

 

Для решения данной задачи можем воспользоваться таблицей конечных разностей, просчитанной в предыдущем примере. Тогда реализуя формулу (19) в нашем случае интерполяционный многочлен Стирлинга примет вид

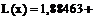t × (0,101625 + 0,091375) / 2+t2×(–0,01025)/ 2 + t×(t2–1)  (–0.00075–0,00075) / 12.

Подставив в данную формулу значение переменной t=-0,8, соответствующее значению переменной х=0,31, получим L(x)=1,804109.

Дата добавления: 2018-04-04; просмотров: 2710; Мы поможем в написании вашей работы!

Поделиться с друзьями:


⇐ Предыдущая12345Следующая ⇒


Мы поможем в написании ваших работ!
.
.
© 2014-2024 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.073)