Определение параметров алгебраического интерполирования с помощью составления системы линейных уравнений
Согласно основному интерполяционному тождеству (1), подставив в (4) узловые значения, можно получить систему уравнений (5)
 .
| (5) |
В матричной форме эта система будет выглядеть A×C=B,
где 
– матрица Ван дер Монда;
; 
.
Решением системы (5) будет вектор С искомых коэффициентов многочлена. Так как определитель матрицы Ван дер Монда всегда отличен от нуля (при xi¹xj), то система (5) будет иметь единственное решение. Его можно найти матричным способом C=A–1×B.
Таким образом, через заданные на интервале [a; b] точки (xi;yi),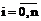 
всегда можно провести единственный интерполяционный многочлен tn(x)= с0+с1x+с2x2+…+сnxn, коэффициенты которого находятся в результате решения системы (5).
П р и м е р. Определить интерполяционный многочлен для функции заданной таблично
| x | 0 | 1 | 2 |
| f(x) | 1 | 1 | 3 |
Решение
Т.к. функция заданная таблично имеет три узловые точки, то степень интерполяционного многочлена будет равна n-1=3-1=2. А значит, его мы можем записать в общем виде, как t2(x)=с0+с1x1+с2x2. Согласно основному интерполяционному тождеству, подставив узловые точки в многочлен получим систему линейных уравнений:
.
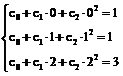Решение данной системы удобно выполнять в математических пакетах Microsoft Excel или MathCAD.
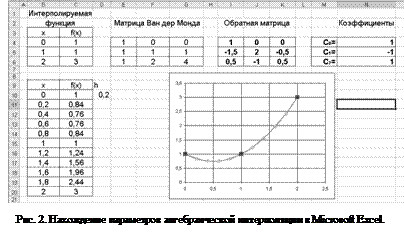
а) Реализация алгебраической интерполяции в Microsoft Excel показана на рис. 2, 3.
б) Реализация алгебраического интерполирования в MathCAD показана на рис. 4.
Значит, искомый многочлен будет иметь вид t2(x)= 1-x+x2 .
|
|
|
Алгебраическое интерполирование с помощью формулы Лагранжа
Интерполирование с помощью систем линейных уравнений является громоздким и зачастую неоправданным. Существует общий подход к построению интерполяционных многочленов. Подберем такую функцию F(х), которая в узловом значении х0 равна 1, а в остальных узлах равна 0, т.е.
F(х0)= 1, F(хi)= 0, хi ≠х0.
Такую функцию мы можем представить в следующем виде
.
Построим многочлен, который в точке х0 принимает значение f(х0), а в остальных узловых точках обращаются в 0. Он будет иметь вид
.
Аналогичным образом определяется многочлен, принимающий значение f(х1) в точке х1, а в остальных узловых точках в 0.
Обобщив результаты, можно записать подобные функции для всех узловых точек, т.е. функции вида
Fj(x)= 
.
Они будут выглядеть
.
Тогда интерполяционный многочлен может быть записан в виде суммы представленных выше многочленов:
| (6) |
Эта формула называется интерполяционной формулой Лагранжа.
В более компактном виде её можно переписать как
 ,
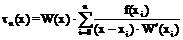| (7) |
где 
;
.
Полином Лагранжа удобно использовать, если требуется находить приближения различных функций заданных в одних и тех же узловых точках. В таких случаях можно предварительно вычислить коэффициенты Лагранжа по формуле
|
|
|
П р и м е р. Составить интерполяционный многочлен для следующих функций заданных таблично, построить их графики.
| x | 0 | 1 | 2 | x | 0 | 1 | 2 | |
| у | 1 | 1 | 3 | у | -5 | 1,45 | 3,76 |
Решение
a) Реализацию формулы Лагранжа для интерполяции функций в Microsoft Excel покажем на рис. 5, 6.
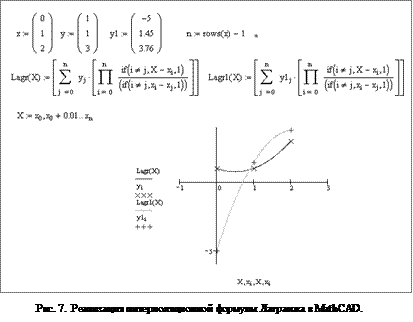б) Реализацию формулы Лагранжа для интерполяции функций в MathCAD покажем на рис. 
7.
Частный случай формулы Лагранжа. Пусть на отрезке 
задана система равноотстоящих узлов 
которыми отрезок делится на 
равных частей 
где 
В этом случае интерполяционный многочлен Лагранжа строится на равноотстоящих узлах и имеет более удобный вид. Преобразуем формулу, введя новую переменную 
, где h= 
. Т.к. для равностоящих узлов xi+1=xi+h, то можем записать:
x=h×t+x0; Þ x-x0=h×t
x–x1= h×t+x0 – x0 –h=(t-1) ×h; Þ x-x1=(t-1)×h
x–x2=x–x1–h= (t-1) ×h –h= x-x2=(t-2) ×h; Þ x-x2=(t-2)×h
Обобщив алгоритм, можем записать, что x-xi=(t-i)×h. (8)
Используя (8) выражение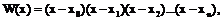 
перепишется в виде:
|
|
|
(9)
Учитывая, что 
найдем:
Обобщив алгоритм, можем записать
(10)
На основании (10) получим:
т.е.
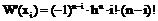. (11)
С учетом (8), (9) и (11) получим частный случай формулы (7) для равноотстоящих узлов:
(12)
1.2.3. Понятие конечных разностей. Связь между конечными разностями и узловыми значениями
Во многих случаях интерполяционный многочлен Лагранжа является громоздким при многократных вычислительных процедурах. Для равноотстоящих узлов или при изменении числа узлов удобнее пользоваться интерполяционными формулами Ньютона.
Введем некоторые понятия.
Пусть таблично задана функция.
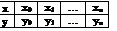
Конечными разностями 1 порядка будем называть выражения вида:
; 2 порядка – 
и т. д.
Как правило, вычисление конечных разностей сводится в таблицу
| х | у | Dу | D2у | D3у | D4у |
| x0 | y0 | ||||
| x1 | y1 | Dy0 | |||
| x2 | y2 | Dy1 | D2y0 | ||
| x3 | y3 | Dy2 | D2y1 | D3y0 | |
| x4 | y4 | Dy3 | D2y2 | D3y1 | D4y0 |
Очевидно, что число конечных разностей на единицу меньше, чем число узлов интерполяционной функции.
Конечные разности многочлена можно выразить через значение функции в узловых точках.
|
|
|
Dy0 =у1–у0
D2y0 = Dy1–Dy0= у2–у1– у1+у0 = у2–2у1+у0
D3y0=D2y1–D2y0=Dy2–Dy1–(у2–2у1+у0)=у3–у2–у1+у1–у2+2у1–у0=у3–у2+3у1– у0.
Продолжая этот процесс можно заметить, что коэффициенты перед соответствующими уi в представлении конечных разностей являются коэффициентами бинома Ньютона: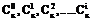 
. Тогда конечные разности в общем виде можно записать
 .
| (13) |
Аналогичным образом можно представить 
.
Часто важнее бывает выразить значения функции через конечные разности:
y1 =у0 + Dy0;
y2 = y1+Dy1=у0+Dу0 +Dу1 = у0+Dу0+Dу0 +Dу1 –Dу0 = у0+2Dу0 +D2у0;
y3 = y2+Dy2= у0+Dу0 +Dу1 +Dу2 = у0+3Dу0+3 D2у0 +D3у0
и т.д.
Заметим, что коэффициенты слагаемых являются коэффициентами бинома Ньютона. Тогда значение функции соответствующей к-ой узловой точке может быть определено по формуле
 .
| (14) |
Дата добавления: 2018-04-04; просмотров: 434; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!