Алгоритм нахождения обратной матрицы для матрицы А

1. Вычисляем det A.

2. Если он равен 0, то обратной матрицы не существует. Если det A не равен 0, считаем алгебраические дополнения .

3. Ставим алгебраические дополнения на соответствующие места.

4. Все элементы получившейся матрицы делим на det A.

Упражнение 1. Выяснить, однозначна ли обратная матрица.

Упражнение 2. Пусть элементы матрицы А — целые рациональные числа. Будут ли элементы обратной матрицы целыми рациональными числами?

Системы линейных уравнений.

Определение 1. Уравнение вида a₁x₁+ ....+a_nx_n=b , где a, ... ,a_n — числа; x₁, ... ,x_n — неизвестные, называется линейным уравнением с n неизвестными.

s уравнений с n неизвестными называется системой s линейных уравнений с n неизвестными, т.е.

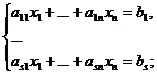
(1)

Матрица А, составленная из коэффициентов при неизвестных системы (1), называется матрицей системы (1).

Если к матрице А добавить столбец свободных членов, то получим расширенную матрицу системы (1).

X = — столбец неизвестных.

— столбец свободных членов.

В матричном виде система имеет вид: AX=B (2).

Решением системы (1) называют упорядоченный набор n чисел (α₁,…, α_n) таких, что если сделаем подстановку в (1) x₁ = α₁, x₂ = α₂,…, x_n = α_n , то мы получим числовые тождества.

Определение 2. Систему (1) называют совместной, если она имеет решения, и несовместной в противном случае.

Определение 3. Две системы называют эквивалентными, если множества их решений совпадают.

Существует универсальный способ решения системы (1) — метод Гаусса (метод последовательного исключения неизвестных), см. [1], стр.15.

Рассмотрим более подробно случай, когда s = n. Существует метод Крамера решения таких систем.

Пусть d = det ,

d_j — определитель d, в котором j–тый столбец заменен столбцом свободных членов.

Теорема (правило Крамера). Если определитель системы d ¹ 0, тогда система имеет единственное решение, получающееся по формулам:

x₁ = d₁/ d …x_n = d_n / d

¢Идея доказательства заключается в том, чтобы переписать систему (1) в форме матричного уравнения. Положим

X = , B =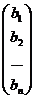

и рассмотрим уравнение AX = B (2) с неизвестной матрицей-столбцом X. Так как A, X, B — матрицы размеров n x n, n x 1, n x 1 соответственно, то произведение прямоугольных матриц АХ определено и имеет те же размеры, что и матрица В. Таким образом, уравнение (2) имеет смысл.

Связь между системой (1) и уравнением (2) заключается в том, что является решением данной системы тогда и только тогда, когда

столбец есть решение уравнения (2).

Действительно, это утверждение означает выполнение равенства

= .

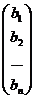
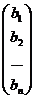Последнее равенство, как равенство матриц, равносильно системе равенств

которое означает, что — решение системы (1).

Итак, решение системы (1) сводится к решению матричного уравнения (2). Так как определитель d матрицы А отличен от нуля, она имеет обратную матрицу А^-1. Тогда АХ = В 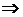А^-1(АХ) = А^-1В 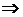(А^-1А)Х = А^-1В 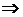ЕХ = =А^-1В 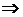Х = А^-1В (3). Следовательно, если уравнение (2) имеет решение, то оно задается формулой (3). С другой стороны, А(А^-1В) = (АА^-1)В = ЕВ = В.

Поэтому Х = А^-1В есть единственное решение уравнения (2).

Так как ,

где А_ij — алгебраическое дополнение элемента a_ij в определителе d, то

= ,

откуда (4).

В равенстве (4) в скобках написано разложение по элементам j-го столбца определителя d_j, который получается из определителя d после замены в нем

j-го столбца столбцом свободных членов. Поэтому, x_j = d_j / d. £

Следствие. Если однородная система n линейных уравнений от n неизвестных имеет ненулевое решение, то определитель этой системы равен нулю.

ТЕМА 3. Многочлены от одной переменной.

Дата добавления: 2018-04-04; просмотров: 250; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 9 10 Следующая ⇒

Мы поможем в написании ваших работ!