Миноры и их алгебраические дополнения

 

     Пусть В — некоторая матрица размером n x n. В =                        ,

  

и k N, 1 ≤ k ≤ n.

Выделим в матрице В k произвольных строк с номерами i₁, i₂, ..., i_k и k произвольных столбцов с номерами j_1, j₂, ..., j_k . Элементы, стоящие на пересечении этих строк и столбцов, образуют матрицу размером k x k. Определитель полученной матрицы называется минором к-того порядка матрицы В. Обозначим его через М. Элементы, не попавшие на пересечение, образуют матрицу размером (n-k) x (n-k). Определитель полученной матрицы называют минором, дополнительным к минору М. Обозначим его через М₁.

Введем еще следующую сумму: S_M = i₁+ i₂+ ...+i_k + j₁+ j₂+ ...+j_k. Сумма S_M — это сумма номеров выделенных строк и выделенных столбцов. Тогда  

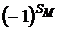 М₁= А_m называется алгебраическим дополнением к минору М.

Существует общий способ сведения вычисления определителей порядка n к вычислению определителей меньших порядков с применением понятия минора и алгебраического дополнения.

     Теорема Лапласа.

     Пусть В Î Р_{n x n} — матрица порядка n, и 1 ≤ k < n. У матрицы В зафиксируем k произвольных строк. Тогда ее определитель равен сумме произведений всех миноров, содержащихся в выделенных строках, на их алгебраические дополнения, т.е. | B | = M₁A₁ + ... + M_sA_s.

     Следствие 1 (разложение определителя по строке). Определитель матрицы В равен сумме произведений элементов какой–нибудь строки на их алгебраические дополнения.

¢Следует из теоремы Лапласа при k = 1. £

     Следствие 1 позволяет сводить вычисление определителя порядка n к вычислению определителей порядка (n - 1).

     Упражнение. Сформулировать теорему Лапласа и следствие 1 в применение к столбцам.

     Следствие 2. Сумма произведений элементов строки определителя матрицы  на соответствующие дополнения к элементам другой строки равна нулю, т.е. .

     Упражнение. Доказать.

     Пример:

 

det                     = det              · det        · (-1)^1+2+1+2 =

 

 

= det   · det           = (-2) · (-3) = 6. 

                

                           

Определитель произведения квадратных матриц.

     Теорема. Пусть А и В — две квадратные матрицы порядка n. Тогда определитель их произведения равен произведению определителей, т.е.

 | AB | = | A| | B |.

¢ Пусть A = (a_ij)_{n x n} , B = (b_ij)_{n x n} . Рассмотрим  определитель d_2n порядка 2n

                                           A

                                           ||    

 

 

 

                       d_2n =

 

 

                                                                  

                                                                                 ||

                                                                             B

 

     d_2n = | A | | B | (-1) ^{1 + ... + n + 1 + ... + n} = | A | | B |.

Если мы покажем, что определитель d_2n равен определителю матрицы С=АВ, то теорема будет доказана.

В d_2n  проделаем следующие преобразования: к 1 строке прибавим (n+1) строку, умноженную на а₁₁; (n+2) строку, умноженную на а₁₂ и т.д. (2n) строку, умноженную на а_1n . В полученном определителе первые n элементов первой строки будут нулями, а n других элементов станут такими:

     a₁₁b₁₁ + a₁₂b₂₁ + ... + a_1nb_n1 = c_11;

     a₁₁b₁₂ + a₁₂b₂₂ + ... + a_1nb_n2 = c_12;

        _...

     a₁₁b_1n + a₁₂b_2n + ... + a_1nb_nn = c_1n.

     Аналогично получаем нули во 2, …, n строках определителя d_2n , причем последние n элементов в каждой из этих строк станут соответствующими элементами матрицы С. В результате, определитель d_2n преобразуется в равный ему определитель:

 

                                                              

 

 

d_2n = | C | (-1) ^{1 + ... + n + ... + 2n} = |AB|. £

     Следствие. Определитель произведения конечного числа квадратных матриц равен произведению их определителей. 

¢ Доказательство проводится индукцией: | A₁ ... A_i+1 | = | A₁... A_i | | A_i+1 | = ... = = | A₁| ... | A_i+1 | . Эта цепочка равенств верна по теореме. £

 

 

Обратная матрица.

     Пусть A = (a_ij)_{n x n} квадратная матрица над полем Р.

     Определение 1. Матрицу А будем называть вырожденной, если ее определитель равен 0. Матрицу А будем называть невырожденной в противном случае.

     Определение 2. Пусть А Î P_n. Матрицу В Î P_n будем называть обратной к А, если АВ = ВА=Е.

     Теорема (критерий обратимости матрицы).Матрица А обратима тогда и только тогда, когда она невырожденная.

¢ Пусть А имеет обратную матрицу. Тогда АА^-1 = Е и, применяя теорему об умножении определителей, получаем | A | | A^-1 | = | E | или | A | | A^-1 | = 1. Следовательно, | A | ¹ 0.

     Пусть, обратно, | A | ¹ 0. Надо показать, что существует матрица В такая, что АВ = ВА = Е. В качестве В возьмем такую матрицу:

         

                                               

                                           В =                                                 ,

 

где А_ij — алгебраическое дополнение к элементу а_ij . Тогда

 

 

АВ =                                                                        

 

 

 

Следует заметить, что в результате получится единичная матрица (достаточно воспользоваться следствиями 1 и 2 из теоремы Лапласа § 6), т.е. АВ = Е. Аналогично показывается, что ВА = Е. £

     Пример. Для матрицы А найти обратную матрицу, или доказать, что ее нет.

 

 

А =

 

 

det A = -3 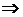 обратная матрица существует. Теперь считаем алгебраические дополнения.

     А₁₁ = -3     А₂₁ = 0       А₃₁ = 6

     А₁₂ = 0      А₂₂ = 0     А₃₂=-3

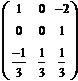
     А₁₃ = 1      А₂₃ = -1    А₃₃ = -1

 

Итак, обратная матрица имеет вид: В =                                       =

 

 

---

Дата добавления: 2018-04-04; просмотров: 288; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!