Упражнение 1. Числовое поле всегда бесконечно

Упражнение 2. Любое числовое поле всегда содержит Q (множество рациональных чисел).

Пример поля отличного от Q, R и C:

K = {a+b , где a и b }.

Тема 2. Матрицы и определители.

Сложение матриц. Умножение матрицы на число.

Пусть К ≠ Æ. Рассмотрим прямоугольную таблицу из n строк и m столбцов, состоящую из элементов К

(1)

a_ij — произвольный элемент таблицы, где i — номер строки, j — номер столбца, a_ij Î К " i,j. Таблицу (1) назовем матрицей размером n x m. Краткая запись (a_ij)_n _x _m_. В будущем будем рассматривать (1) над числовыми полями. Матрицы будем обозначать A,B,C, а их элементы соответственно a_ij , b_ij, c_ij .

Определение 1. Две матрицы (a_ij), (b_ij ) одинаковых размеров будем называть равными, если a_ij = b_ij " i,j.

Определение 2. Матрица называется квадратной, если m=n.

Определение 3. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали, равны 0.

Пример:

Определение 4. Диагональная матрица, все элементы которой равны между собой, называется скалярной матрицей.

Скалярная матрица, у которой элемент, стоящий на диагонали равен 1, называется единичной.

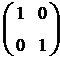Пример:

Сложение матриц и их свойства.

Пусть n и m — фиксированные натуральные числа. Рассмотрим множество матриц над некоторым числовым полем Р размером n x m, обозначим его Р_n _x _m .

Определение 5. Возьмем две матрицы A, BÎ Р_n _x _m_.Под суммой матриц A и B (обозначают А+В) понимают матрицу С Î Р_n _x _m такую, что c_ij =a_ij + b_ij_.для всех i=1,…,n; j=1,…,m.,т.е. чтобы сложить две матрицы, надо сложить элементы, стоящие на одинаковых местах.

Свойство 1. Сложение матриц ассоциативно, т.е. (А+В)+С = А + (В+С) и коммутативно, т.е. А+В=В+А, .

¢ Доказательство следует из соответствующих свойств для чисел. £

Свойство 2. Если нулевую матрицу прибавить к произвольной матрице тех же размеров, то последняя не изменится.

Свойство 3. Для любой матрицы A Î Р_n _x _m $ B Î Р_n _x _m такая, что А+В=0. Такая матрица В называется противоположной к матрице А.

Умножение матрицы на число и его свойства.

Определение 6. Пусть А Î Р_n _x _m , a Î Р — произвольный элемент поля Р. Под произведением aА понимают матрицу В тех же размеров такую, что b_ij = a a_ij.

Свойство 1. 1А = А .

Свойство 2. (a+b) А = aА + bА. (Умножение матрицы на число дистрибутивно относительно сложения чисел) .

Свойство 3. a (А + В) = aА + aВ. (Умножение числа на сумму матриц дистрибутивно относительно сложения матриц) .

Свойство 4. (ab) А = a (bА) .

¢ Доказательство проводится сравнением элементов матриц левой и правой частей равенства. Например, рассмотрим свойство 2. Известно, что (a+b)a_ij = a a_ij + b a_ij, где a_ij — произвольный элемент матрицы А,(дистрибутивность умножения относительно сложения элементов поля). £

Умножение матриц.

Мы никак не мотивировали операцию сложения матриц, но едва ли это вызвало недоумение в силу своей естественности. Операция умножения матриц уже не обладает этим качеством.

Пусть A = (a_ij)_m _x _n , B = (b_ij)_n _x _p. Под произведением АВ понимают

матрицу С с элементами c_ij = .

АВ := С= (с_ij)_m _x _p.

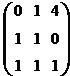
Например, А = и В = .

Тогда AВ =

5=1 · 0 + 2 · 1 + 3 · 1

6=1 · 1 + 2 · 1 + 3 · 1

7= 1 · 4 + 2 · 0 + 3 · 1 и т.д.

Берется i-тая строка матрицы А и j-тый столбец матрицы В, перемножаются покомпонентно и результаты складываются. Это есть элемент матрицы С на позиции i,j.

Свойство. Произведение матриц не коммутативно, т.е. АВ ¹ ВА, в том числе и квадратных.

Дата добавления: 2018-04-04; просмотров: 263; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!