Основные понятия и определения 4 страница
Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью 
находится между границами доверительного интервала 
.
Половина длины доверительного интервала 
называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р=0.95 или Р=0.995 и по формулам
определяют соответствующее значение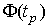 
интегральной функции нормированного нормального распределения. Затем по данным находят значение коэффициента 
и вычисляют доверительное отклонение . Проведение многократных наблюдений позволяет значительно сократить доверительный интервал. Действительно, если результаты наблюдений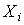 
(i=l, 2,..., n) распределены нормально, то нормально распределены и величины 
, а значит, и среднее арифметическое 
, являющееся их суммой. Поэтому имеет место равенство.
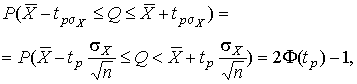
где 
определяется по заданной доверительной вероятности Р.
Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в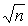 
раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.
|
|
|
Половина длины нового доверительного интервала
| (5.3) |
называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде
Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением
| (5.4) |
называемым дробью Стьюдента. Входящие в нее величины и 
вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений.
Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением:
| (5.5) |
где S(t, k)- плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна n - 1. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале 
, согласно выражению (5.5), вычисляется по формуле
или, поскольку S(t, k)является четной функцией аргумента t,
|
|
|
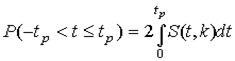
Подставив вместо дроби Стьюдента tее выражение через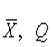 
и 
, получим окончательно
| (5.6) |
Величины 
, вычисленные по формулам (5.5) и (5.6), были табулированы Фишером для различных значений доверительной вероятности Рв пределах 0.10 - 0.99 при 
В табл.5.1 приведены значения 
для наиболее часто употребляемых доверительных вероятностей Р.
Таким образом, с помощью распределения Стьюдента по формуле (5.6) может быть найдена вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает 
, например 
и т.д. Итог измерений записывается в виде
ПРИМЕР
При измерении ЭДС нормального элемента полечены следующие результаты:
| N опыта | 1 | 2 | 3 | 4 | 5 | 6 |
| ЭДС | 1,018456 | 1,018452 | 1,018453 | 1,018457 | 1,018455 | 1,018457 |
| N опыта | 7 | 8 | 9 | 10 | 11 | 12 |
| ЭДС | 1,018521 | 1,018456 | 1,018455 | 1,018454 | 1,018458 | 1,018457 |
Приняв доверительную вероятность р=0.99, определить результат, оценить случайную и относительную погрешности.
Для решения данной задачи предлагается следующая методика:
1. определяется неисправленный результат измерения
2. определяется относительная погрешность неисправленного результата измерений
3. вычисляем СКО погрешности неисправленного результата
|
|
|
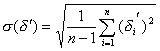
3. исключаем явные промахи (аномальные результаты). Они не должны удовлетворять условию:
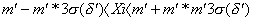
После исключения промахов (допустим, что их количество получилось r ) определяем те же величины для исправленного результата измерений.
Математическое ожидание:
Относительная погрешность:
СКО результата:
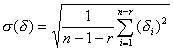
Вычисляем результат измерений, как:
,
где tp - коэффициент Стьюдента.
Некоторые значения коэффициентов Стьюдента приведены в таблице:
Таблица 5.1
| Число измерений | Доверительная вероятность | ||
| 0.9 | 0.95 | 0.99 | |
| 2 | 6,31 | 12,72 | 63,7 |
| 3 | 2,92 | 4,3 | 9,92 |
| 4 | 2,35 | 3,18 | 5,84 |
| 5 | 2,13 | 2,78 | 4,6 |
| 6 | 2,02 | 2,57 | 4,03 |
| 7 | 1,94 | 2,48 | 3,71 |
| 8 | 1,9 | 2,37 | 3,5 |
| 9 | 1,86 | 2,31 | 3,36 |
| 10 | 1,83 | 2,26 | 3,25 |
| 15 | 1,75 | 2,15 | 2,92 |
| 20 | 1,72 | 2,08 | 2,84 |
| 30 | 1,7 | 2,05 | 2,73 |
| Более 30 | 1,65 | 1,96 | 2,58 |
По приведенной методике определяем математическое ожидание неисправленного результата:
m’=12.221531/12=1.0184609.
Определяем относительную погрешность неисправленного результата 
i’:
| 1’
| -4.8*10-6 | 5’
| -5,79*10-6 | 9’
| -5,79*10-6 |
| 2’
| -8.74*10-6 | 6’
| -3,83*10-6 | 10’
| -6,77*10-6 |
| 3’
| -7,76*10-6 | 7’
| 5,9*10-5 | 11’
| -2,85*10-6 |
| 4’
| -3,83*10-6 | 8’
| -4,8*10-6 | 12’
| -3,83*10-6 |
Определяем СКО неисправленного результата:
( ')=1,865*10-5.
Определяем границы, в которых находится результат измерения (выявляем явные промахи):
|
|
|
m’-m’*3 ( ')=1.0184039
m’+m’*3 ( ')=1.0185179.
По результатам измерений делаем вывод, что измерение № 7 является явным промахом и должно быть исключено из вычислений.
Определяем математическое ожидание исправленного результата:
m=1.0184553.
Определяем относительную погрешность исправленного результата di:
| 1
| 6.873*10-7 | 5
| -2.95*10-7 | 9
| -2.95*10-7 |
| 2
| -3.24*10-6 | 6
| 1.67*10-6 | 10
| -1.87*10-7 |
| 3
| -2.26*10-6 | 7
| -“- | 11
| 2.65*10-6 |
| 4
| 1.67*10-6 | 8
| 6.873*10-7 | 12
| 1.67*10-6 |
Определяем СКО исправленного результата:
( ')=1,837*10-6.
Определяем результат измерения:
Х=1.837±5.7*10-8, при доверительной вероятности р=0.99.
Моменты случайных погрешностей
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.
Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами.
Начальным моментом n-го порядка результатов наблюдений называется интеграл вида
| (6.1) |
представляющий собой математическое ожидание степени 
.
При n=1
т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений.
Центральным моментом n-го порядка результатов наблюдений называется интеграл вида
| (6.2) |
Вычислим первый центральный момент:
| (6.3) |
Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю.
Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений.
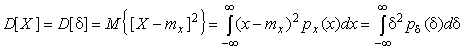
| (6.4) |
При n=2
Дисперсия D[X] случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания.
Если математическое ожидание результатов наблюдений можно рассматривать в механической интерпретации как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести.
Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическимотклонением результатов наблюдений:
| (6.5) |
С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины 
, т. е. вероятность 
. Для этого рассмотрим формулу, известную как неравенство Чебышева:
или 
Полагая 
, можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т. е. вероятность того, что случайная погрешность окажется больше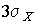 
:
Дата добавления: 2018-02-28; просмотров: 259; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!