Основные понятия и определения 2 страница
Предположим, что (ti) = 0,т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины - как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней.
(ti) = 0,т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины - как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней.
В этих условиях случайная погрешность измерений  o определяется как разность между исправленным результатом Х измерения и истинным значением А измеряемой величины:
o определяется как разность между исправленным результатом Х измерения и истинным значением А измеряемой величины:

| (2.3) |
причем исправленным будем называть результат измерений, из которого исключены систематические погрешности.
При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.
Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами.
Погрешности измерений.
Основные виды.
При анализе значений, полученных при измерениях, следует разграничивать два понятия: истинные значения физических величин и их опытные проявления - результаты измерений.
Истинные значения физических величин - значения, идеальным образом отражающие свойства данного объекта, как в количественном, так и в качественном отношении. Они не зависят от средств нашего познания и являются абсолютной истиной.
Результаты измерений, - представляют собой приближенные оценки значений величин, найденные путем измерения, они зависят не только от них, но еще и от метода измерения, от технических средств, с помощью которых проводятся измерения, и от восприятия наблюдателя, осуществляющего измерения.
Разница 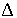 между результатами измерения X' и истинным значением А измеряемой величины называется абсолютной погрешностью измерения:
между результатами измерения X' и истинным значением А измеряемой величины называется абсолютной погрешностью измерения:
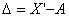
| (2.4) |
Абсолютная погрешность, взятая с обратным знаком, называется поправкой измерительного прибора.
Относительная погрешность  измерений: - отношение абсолютной погрешности к истинной величине. Определяется, как правило, в %.
измерений: - отношение абсолютной погрешности к истинной величине. Определяется, как правило, в %.
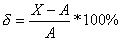
| (2.5) |
Приведенная погрешность 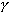 измерения: - отношение абсолютной погрешности к некоторому нормированному значению Хn
измерения: - отношение абсолютной погрешности к некоторому нормированному значению Хn
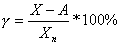
| (2.6) |
Основная погрешность измерительного прибора: - погрешность, возникающая при нормальном использовании прибора. Её можно представить в виде суммы погрешностей - аддитивной и мультипликативной.
 =a+bX, =a+bX,
| (2.7) |
где а – аддитивная погрешность;
b – мультипликативная погрешность;
Х – текущее значение измерений.
Аддитивная погрешность – не зависит от чувствительности прибора и является постоянной для всего диапазона измерений.
Мультипликативная погрешность – зависит от чувствительности прибора и изменяется прпорционально текущему значению входной величины.
Интерпритация сказанного приведена на рисунке 2.1.
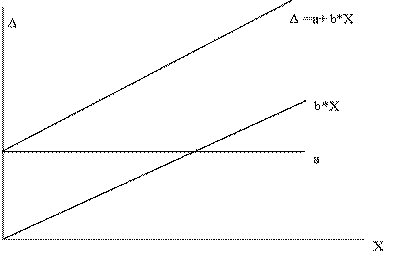
рис. 2.1.
Но поскольку истинное значение А измеряемой величины неизвестно, то неизвестны и погрешности измерения, поэтому для получения хотя бы приближенных сведений о них приходится в формулу (1) вместо истинного значения подставлять так называемое действительное значение.
Действительным значением физической величины - называется ее значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него.
В качестве причин возникновения погрешностей являются: несовершенство методов измерений, технических средств, применяемых при измерениях, и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений.
У измерительных приборов, как правило, нормируется основная приведенная погрешность во всем диапазоне измерений, которая называется классом точности прибора. В соответствии с ГОСТ 8.401-80 классы точности выбирают из ряда: 1*10n ; 1.5*10n ; 2*10n ; 2.5*10n ; 4*10n ; 5*10n ; 6*10n, где n=1, 0, -1, -2, -3, ... .
У цифровых измерительных приборов погрешность определяется из выражения:
 , ,
| (2.8) |
где Хк – конечное значение диапазона измерения,
Х – текущее значение измеряемой величины,
c и d – составляющие погрешности, приведенные на шкале или в паспорте цифрового прибора.
 ОБРАБОТКА ПОГРЕШНОСТЕЙ.
ОБРАБОТКА ПОГРЕШНОСТЕЙ.
Если результат измерения определяется как совместное измерение, тогда погрешность результата можно определитть воспользовавшись таблицей:
| Функция | Погрешности | |
 - абсолютная погрешность - абсолютная погрешность
|  - относительная погрешность - относительная погрешность
| |
| X+Y+Z | 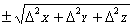
| 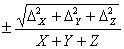
|
| X-Y | 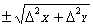
| 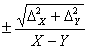
|
| X*Y | 
| 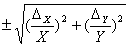
|
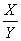
| 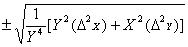
| 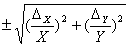
|
| Xn | ± n*Xn-1*  x x
| 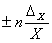
|
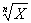
| 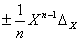
| 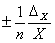
|
| Sin X | ± cos X  x x
| ± ctg X  x x
|
| Cos X | ± sin X  x x
| ± tg X  x x
|
| Tg X | 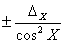
| 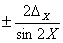
|
| Ctg X | 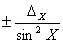
| 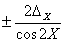
|
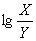
| 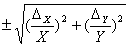
| 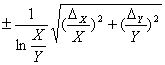
|
| Arctg X | 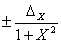
| 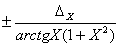
|
Описанные причины возникновения погрешностей определяются совокупностью большого числа факторов, под влиянием которых складывается суммарная погрешность измерения - см. формулу (1). Их можно объединить в две основные группы.
1. Факторы, постоянные или закономерно изменяющиеся в процессе измерительного эксперимента, например плавные изменения влияющих величин или погрешности применяемых при измерениях образцовых мер. Составляющие суммарной погрешности (1), определяемые действием факторов этой группы, называются систематическими погрешностями измерения. Их отличительная особенность в том, что они остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины. До тех пор, пока систематические погрешности больше случайных, их зачастую можно вычислить или исключить из результатов измерений надлежащей постановкой опыта.
2. Факторы, проявляющиеся весьма нерегулярно и столь же неожиданно исчезающие или проявляющиеся с интенсивностью, которую трудно предвидеть. К ним относятся, например, перекосы элементов приборов в их направляющих, нерегулярные изменения моментов трения в опорах, малые флюктуации влияющих величин, изменения внимания операторов и др.
Доля, или составляющая, суммарной погрешности измерения (1), определяемая действием факторов этой группы, называется случайной погрешностью измерения. Ее основная особенность в том, что она случайно изменяется при повторных измерениях одной и той же величины.
При создании измерительной аппаратуры и организации процесса измерения в целом интенсивность проявления большинства факторов данной группы удается свести к общему уровню, так что все они влияют более или менее одинаково на формирование случайной погрешности. Однако некоторые из них, например внезапное падение напряжения в сети электропитания, могут проявиться неожиданно сильно, в результате чего погрешность примет размеры, явно выходящие за границы, обусловленные ходом эксперимента в целом. Такие погрешности в составе случайной погрешности называются грубыми. К ним тесно примыкают промахи - погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов.
Таким образом, мы имеем два типа погрешностей измерения:
- систематические погрешности, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях.
- случайные (в том числе грубые погрешности и промахи), изменяющиеся случайным образом при повторных измерениях одной и той же величины;
В процессе измерения оба вида погрешностей проявляются одновременно, и погрешность измерения можно представить в виде суммы:
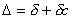
| (3.1) |
где  с- случайная, а
с- случайная, а  - систематическая погрешности.
- систематическая погрешности.
Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей математической обработкой опытных данных. Поэтому наибольшее значение имеет изучение погрешности как функции номера наблюдения, т. е. времени D(t). Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции:
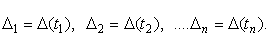
| (3.2) |
В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале.
Предположим, что  (ti)=0, т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины - как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней.
(ti)=0, т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины - как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней.
В этих условиях случайная погрешность измерений dc определяется как разность между исправленным результатом Х измерения и истинным значением А измеряемой величины:
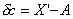
| (3.3) |
причем исправленным будем называть результат измерений, из которого исключены систематические погрешности.
При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.
Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТИ.
Следует считать, что если событие может произойти, то оно обязательно произойдет. Все решает только вопрос времени. Возможность происхождения события в данный момент характеризуется вероятностью происхождения события – р. Если, например, событие А может происходить независимо от всех других событий – оно называется независимым, обозначается р(А) и не может превышать 1.

Вероятность осуществления события А называется в этом случае безусловной вероятностью.
Вероятность того, что событие А не произойдет, обозначается р( 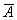 ).
).
р( 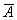 )=1-р(А).
)=1-р(А).
Если событие А не может произойти вне зависимости от события В, то оно называется зависимым.
Вероятность осуществления события А при условии, что произошло событие В, обозначается р(A/B) и называется условной вероятностью события А.
Если события А и В независимы друг от друга, то имеет место математическая запись:
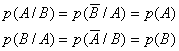
Степень зависимости событий оценивается коэффициентами регрессии и корреляции.
Коэффициент регрессии события А относительно события В записывается как:
r(А,В)=р(А/В)-р(А/  )
)
Коэффициент регрессии события В относительно события А записывается как:
r(В,А)=р(В/А)-р(В/ 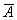 ).
).
Коэффициент корреляции (совпадений) событий А и В выражается формулой:
К(А,В)= 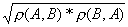
В том случае, если результаты опыта сводятся к схеме случая и общее число случаев (опытов) равно N, то вероятность события А выражается как:
р(А)= NA /N,
где NA-число случаев благоприятных событию А (или число случаев, при которых событие А произошло).
Для достоверной оценки вероятности проявления события необходимо провести ряд опытов, количество которых определяет степень достоверности результата. В метрологии принято считать, что если произведено 30 или более опытов, то ряд называется репрезентативным или представительным. Если опытов было меньшее количество, то ряд называют нерепрезентативным (не представительным).
Описание случайных погрешностей с помощью функций распределения
Рассмотрим результат наблюдений Х за постоянной физической величиной Q как случайную величину, принимающую различные значения Z, в различных наблюдениях за ней. Значения 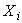 будем называть результатами отдельных наблюдений.
будем называть результатами отдельных наблюдений.
Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения.
Дата добавления: 2018-02-28; просмотров: 289; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
