Критерий Ходжа-Лемана относительно рисков

 

 

	Пj	П1	П2	…	Пn
	Аi
	А1	r11 q1	r12 q2	…	r1n qn
R (HL) =	А2	r21 q1	r22 q2	…	r2n qn
	…	…	…	…	…
	Аm	rm q1	rm2 q2	…	rmn qn
	qj	q1	q2	…	qn

 

 

Критерий Ходжа-Лемана относительно рисков опирается одновременно на критерий Байеса и критерий Сэвиджа.

Показателем неэффективности чистой стратегии А_i по критерию Ходжа-Лемана относительнорисков (HL^r) является:

 

HL ri

=ƛBir (q) + (1-ƛ) S i, i = 1,2,..., m

 

где

B_i(q) –показатель неэффективности стратегии А_i покритерию Байеса относительно рисков с вектором q = (q₁, q₂,…,q_n) распределения вероятностей состояний природы,который определяется по формуле:

n
B r ∑	q j	rij
j=1

 

S_i –показатель неэффективности стратегии А_i по критериюСэвиджа с вектором q = (q₁, q₂,…,q_n) распределения вероятностей состояний природы, который определяется по формуле:

S i

=max rij

 

Ценой игры в чистых стратегиях по критерию Ходжа-Лемана относительно рисков является минимальное значение среди показателей неэффективности чистой стратегии А_i по критерию Ходжа-Лемана относительно рисков:

HL ri=

ƛBir (q) + (1-ƛ) S i, i = 1,2,..., m

 

Пример:

 

Тип		Спрос
товара	П1	П2	П3
А1
А2
А3

 

Найти оптимальную стратегию по критерию Ходжа-Лемана относительно рисков при λ = 0,6 и при вероятностях состояний природы

q₁ = 0,2; q₂ = 0,3; q₃ = 0,5

 

 

 

41.Основные понятия и определения в теории бескоалиционных неантагонистических игр.

 

Некооперативная или бескоалиционная игра, это система Г= (a_ij,b_ij)=(H^a(A_i,B_j), H^b(A_i,B_j)), где A_i и B_j принадлежат Sa и Sb соответственно, а H^a и H^b функции выигрыша. Sa и Sb – множество стратегий игрока А и В Sa= {A1,A2, …, Am}, Sb = {B1,B2, …, Bn}.

Бескоалиционное поведение, когда соглашения между участниками запрещены правилами, а кооперативное поведение разрешается в форме выбора совместных стратегий.

Интересы игроков могут пересекаться, быть взаимовыгодными обоим игрокам, в то время как в антагонистическом конфликте это не представляется возможным.

Матрица выигрышей двух игроков в бескоалиционной игре имеет следующий вид S= S^a x S^b:

А\В	B1	…	Bn
A1	(a11,b11)	…	(a1n,b1n)
…	…	…	…
Am	(am1,bm1)	…	(amn,bmn)

 

Неантагонистические игры, как и антагонистические, могут быть как конечные, так и бесконечные. Эта характеристика игры зависит от количества чистых стратегий игроков (S₁, S₂, …,S_k где k- количество игроков, конечны)

Способы задания игр:

· стратегическая(нормальная, матричная)

· позиционная форма (форма дерева)

 

 

42.Стратегическая форма игры. Чистые и смешанные стратегии игроков в бескоалиционных неантагонистических играх. Функции выигрышей игроков. Доминирование стратегий.

 

Описание игры в нормальной (стратегической) форме включает три элемента: множество игроков, множество чистых стратегий каждого игрока, множества платёжных функций каждого игрока. Таким образом, игру в нормальной форме можно представить в виде L -мерной матрицы, элементами которой являются L -мерные игровые ситуации.

Определение 8.1. Игрой в нормальной (стратегической) форме называется набор объектов вида

В (8.1) – обозначение игры, – множество игроков, – множество чистых стратегий игрока , – функция выигрыша игрока , принимающая вещественные значения. Значение функции выигрыша представляет собой выигрыш, который получает игрок , если игроками используются стратегии , .

Игра происходит следующим образом. Игроки одновременно и независимо друг от друга (не имея информации о действиях других игроков) выбирают свои стратегии из множества всех своих возможных стратегий . В результате формируется набор стратегий

называемый в теории игр ситуацией. В (8.2) символ означает декартово произведение множеств . При этом само множество именуют множеством всех ситуаций в данной игре.

После выбора стратегий игроками игра прекращается, и каждый игрок получает выигрыш, который вычисляется как значение его функции выигрыша в этой ситуации , т.е. величину .

Смешанной стратегией игрока будем считать полный набор вероятностей применения этим игроком своих чистых стратегий 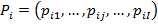, – количество стратегий у игрока .

Определение 8.2. Говорят, что стратегия игрока в игре доминирует стратегию этого игрока, если для всех 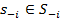выполнено неравенство

И хотя бы для одного 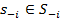справедливо строгое неравенство

Перефразируя определение 8.2, получаем, что одна стратегия игрока доминирует другую стратегию этого же игрока, если при использовании игроком этой стратегии его выигрыш не меньше, чем при использовании другой стратегии независимо от стратегий других игроков, при этом найдутся такие стратегии других игроков, что этот выигрыш окажется строго больше.

 

43.Равновесие по Нэшу в чистых стратегиях и смешанных стратегиях. Логико-эвристический подход к нахождению равновесных по Нэшу игровых ситуаций. Определение лучших ответов игрока на действия противника на основе функции выигрыша.

 

Этот принцип определяет в качестве оптимальных такие ситуации, для которых любые индивидуальные отклонения игроков от входящих в эту ситуацию стратегий, не могут увеличить выигрыша отклонившегося игрока при условии, что все остальные игроки придерживаются зафиксированных в этой ситуации стратегий. Математически это условие выражается следующим образом.

Определение 8.5. Ситуация

в игре называется равновесием по Нэшу, если для каждого игрока и любой стратегии этого игрока выполняется неравенство

или

В смешанных стратегиях равновесие Нэша определяется аналогично:

Из определения 8.3 следует, что если стратегия игрока входит в ситуацию равновесия, то на ней достигает максимума его функция выигрыша, при условии, что остальные игроки придерживаются стратегий, входящих в ситуацию равновесия.

Рассмотрим игру в нормальной форме. Обозначим через – множество наилучших ответов игрока на поведение других игроков :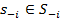

Множество наилучших ответов игрока содержит все стратегии этого игрока, на которых достигается максимум его функции выигрыша, при условии, что ему известны выбранные стратегии других игроков.

Аналогично определяется множество лучших ответов в смешанных стратегиях:

 

 

---

Дата добавления: 2015-12-21; просмотров: 126; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!