Критерий Гермейера оптимальности чистых стратегий
При использовании этого критерия исходная платёжная матрица заменяется матрицей Гермейера. Каждый элемент матрицы мы домножаем на соответствующую вероятность j состояния природы.
 для матрицы выигрышей,
для матрицы выигрышей,
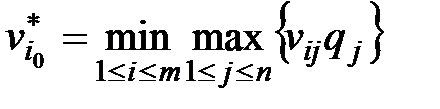 для матрицы потерь.
для матрицы потерь.
Критерий Гермейера применяют игроки не склонные к риску, т.к. каждая стратегия оценивается с точки зрения min по гарантиров. результата.
Состояние природы образует минимум а затем игрок выбирает стратегию которая принесёт ему максимальный результат. Т.е. он защищает себя.
1) Пусть матрица А является матрицей выигрышей игрока А.
2) Даны вероятности qi=p(Пj), j=1,…,n, состояний природы Пj, j=1,…,n, удовлетворяющие условию (1).
Т.о. игрок А находится в ситуации принятия решений в условиях риска
3) Положим l=1 и

| (15) |
Таким образом, матрица В представляет собой вектор столбец
| В= | 
|
размера m x 1.
4) Полагаем l1=1. Условие (2), очевидно, выполняется.
5) Показатель эффективности стратегии Аi по критерию Гермейера определяем по формуле (3) с учетом (15) и того, что l1=1:

| (16) |
Если игрок А придерживается стратегии Аi, то вероятность выигрыша aij при этой стратегии и при состоянии природы Пj равна, очевидно, вероятности qj этого состояния природы. Поэтому формула (16) показывает, что показатель эффективности стратегии Аi по критерию Гермейера есть минимальный выигрыш при этой стратегии с учетом его вероятности.
6) Цена игры по критерию Гермейера определяется по формуле (4):
|
|
|
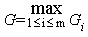
7) Оптимальной стратегией по критерию Гермейера считается стратегия Аk с наибольшим показателем эффективности:
Gk= G
Заметим, что критерий Гермейера можно интерпретировать как критерий Вальда, применимый к игре с матрицей

Критерий Гермейера так же, как и критерий Вальда является критерием крайнего пессимизма игрока А, но, в отличие от критерия Вальда, игрок А, принимая решение с максимальной осмотрительностью, учитывает вероятности состояний природы.
В случае равномерного распределения вероятностей состояний природы: qj=n-1, j=1,…,n, показатель эффективности стратегии Аi, в силу формулы (16), будет равен Gi=n-1aij и, следовательно, критерий Гермейера эквивалентен критерию Вальда, т.е. стратегия, оптимальная по критерию Гермейера, оптимальна и по критерию Вальда, и наоборот.
Пример.
Исходная матрица
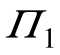 , q=0,4 , q=0,4
|  , q=0,2 , q=0,2
|  , q=0,1 , q=0,1
| |

| |||

| |||
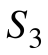
|
Далее умножаем каждый элемент в столбце на соответствующий коэффициент q. Получим следующую таблицу:
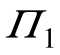 , q=0,4 , q=0,4
|  , q=0,2 , q=0,2
|  , q=0,1 , q=0,1
| VGi в. | VGi п. | |

| 3,6 | 0,8 | 0,1 | 0,1 | 3,6 |

| 2,8 | 0,2 | 0,8 | 0,2 | 2,8 |
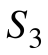
| 4,4 | 0,6 | 0,7 | 0,6 | 4,4 |
В столбце VGi в. Находим миним. Элементы по строкам, а в столбце VGi п. находим макс. Элементы.
|
|
|
Далее находим VGi в (maxmin), и VGi п. (minmax)
Получаем следующий ответ: S*=S3, V*=0,6 - выигрыш
S*=S2, V*=2,8 - потеря
Дата добавления: 2015-12-21; просмотров: 81; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
