Приложение 5. Определение коэффициентов функциональной зависимости 2 страница
Ответ: предельная адсорбция G ¥ = 7.04 мкмоль/м2
площадь молекулы в насыщенном слое s m = 0.236 нм2.
Пример 2. (Тема: адсорбция на твёрдых поверхностях) В следующей ниже таблице приведены результаты экспериментального измерения изотермы адсорбции азота на силикагеле. Найдите из этих данных удельную поверхность силикагеля методом БЭТ, приняв площадь молекулы азота в насыщенном мономолекулярном слое равной 16.2 Å2.
| p / p S | 0.008 | 0.025 | 0.034 | 0.067 | 0.075 | 0.083 |
| V, см3/г | ||||||
| p / p S | 0.142 | 0.183 | 0.208 | 0.275 | 0.333 | 0.375 |
| V, см3/г |
V – объём адсорбированного азота, приведённый к нормальным условиям,
p / p S – относительное давление азота,
p S – давление насыщенного пара азота при температуре измерений.
Решение. Удельная площадь поверхности адсорбента находится из числа молей n m в насыщенном мономолекулярном слое по уравнению:
S уд = n m N A s m (1)
где s m – площадь, занимаемая молекулой в насыщенном слое (в обиходе её часто называют "посадочной площадкой", тогда как n m называется ёмкостью монослоя). Число молей адсорбированного газа можно выразить через объём адсорбированного газа:
n m = V m/ V 0 (2)
где V 0 – молярный объём идеального газа при нормальных условиях, V m – объём, который должен быть адсорбирован для заполнения монослоя. Таким образом:
S уд = V m N A s m/ V 0 (1а)
В теории БЭТ, зависимость адсорбции от относительного давления даётся уравнением:
|
|
|
где с – параметр, зависящий от температуры.
Для практических вычислений это теоретическое уравнение обычно преобразуют к более удобному виду
(3)
или
(3а)
так как объём, при прочих равных условиях, пропорционален числу молей.
Уравнения (3) и (3а) являются линейными вида
y = a + bx
где
, 
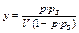, а = 
, 
Интересующий нас параметр V m может быть найден алгебраически из коэффициентов а и b:
V m = (a + b)–1 (4)
Таким образом, общий план решения задачи состоит в следующем: вычисляем величины х и у из численных данных в таблице, строим график зависимости у от х, из которого определяем коэффициенты а и b, вычисляем V m по уравнению (4) и затем S уд по уравнению (1а).
Вычисления удобно вести в отдельной таблице, как показано ниже. В первых двух столбцах воспроизведены значения, данные в условии, и в третьем столбце – вычисленные значения у, которые для удобства переведены в единицы мг/см3. Из графика находим а = 0.04 мг/см3 и b = 16.34 мг/см3. Тогда по уравнениям (4) и (1а) получается
V m = (0.04 + 16.34)–1 = 6.1×10–2 см3/мг = 6.1×10–5 м3/г
S уд = 
= 2.7×102
с единицами измерения:
= м2/г
| V, см3/г | p / p S º х | у, мг/см3 |
| 0.008 | 0.183 | |
| 0.025 | 0.493 | |
| 0.034 | 0.617 | |
| 0.067 | 1.177 | |
| 0.075 | 1.267 | |
| 0.083 | 1.393 | |
| 0.142 | 2.364 | |
| 0.183 | 2.909 | |
| 0.208 | 3.367 | |
| 0.275 | 4.462 | |
| 0.333 | 5.547 | |
| 0.375 | 6.250 |
|
|
|
|
Пример 3. (Тема: равновесие седиментации в центробежном поле) Вычислить молярную массу белка серум глобулина по следующим данным о равновесном центрифугировании его раствора. Плотность растворителя 1.0077 г/см3, удельный парциальный объём белка в растворе 0.745 см3/г, температура 291 К, число оборотов ротора центрифуги 6920 мин–1. Концентрация на расстоянии от оси вращения ротора 4.63 см – 0.189 вес. %, на расстоянии 4.68 см – 0.215 вес. %.
Решение. Если система вращается вокруг некоторой оси с постоянной угловой скоростью w, то потенциальная энергия частицы с массой m равна E = E 0 - m w2 x 2/2, где x – расстояние от оси вращения, m w2 x 2/2 – кинетическая энергия частицы, Е 0 – полная энергия частицы, равная потенциальной энергии на нулевом расстоянии, то есть на оси вращения. Поэтому распределение Больцмана для такой системы имеет вид
(1)
где n – численная концентрация (число частиц в единице объёма) на расстоянии x, n0 – то жена расстоянии x = 0.
В растворе, молекулы с разной массой вынуждены конкурировать между собой. То есть, более тяжёлые молекулы (молекулы белка) вытесняют более лёгкие молекулы (молекулы растворителя). Поэтому, если это уравнение применяется к растворённому белку, то n и n0 - концентрация молекул белка, а масса m эфф – эффективная масса молекулы белка, которая равна массе молекулы белка в вакууме за вычетом массы растворителя, вытесняемого молекулой белка: m эфф = m – m растворитель. По условию задачи требуется найти молярную массу белка М, то есть массу N A "штук" молекул белка в вакууме. Таким образом, цель задачи найти величину
|
|
|
М = N A× m (2)
Масса растворителя, вытесняемого молекулой белка, может быть представлена как произведение объёма молекулы белка на плотность растворителя, m растворитель = V ×r0. Объём единичной молекулы белка не известен, но в условии дан удельный парциальный объём белка (V уд), который равен V уд = V / m. Отсюда следует, что m растворитель = V ×r0 = m × V уд×r0 и m эфф = m – m растворитель = m – m × V уд×r0. То есть
m эфф= m (1 – V уд×r0). (3)
(Заметим, что множитель (1 – V уд×r0) имеет в физической химии специальное название – коэффициент или фактор "всплытия")
Уравнения (1) и (2) показывают, как уравнение Больцмана связано с искомой молярной массой. Чтобы найти эффективную массу необходимо составить систему двух уравнений Больцмана для двух данных расстояний x (4.63 и 4.68 см) и исключить неизвестную концентрацию n0:
|
|
|
Избавимся от n0, поделив одно уравнение на другое:
и решим полученное уравнение относительно эффективной массы
. (4)
Угловую скорость в этом уравнении следует выразить через число оборотов ротора центрифуги (w = 2p n), а численную концентрацию – через содержание в весовых процентах, поскольку именно процентное содержание дано в условии задачи. Для последнего перевода учтем, что процентная концентрация, Р, – это содержание растворённого вещества (граммы) в 100 г раствора, или содержание Р / М молей растворённого вещества (где М – молярная масса растворённого вещества) в 100/r см3 раствора (где r - плотность раствора). Иначе, это – N A P / M молекул в объёме 100/r см3 раствора. Таким образом, число молекул n в 1 см3 раствора составляет n = r N A P /100 M. Отсюда следует
(из этого уравнения ясно, что с равным успехом можно рассматривать число молекул в объёме 1 л, 1 м3 и т.д. – это не имеет значения в данной задаче). Поскольку концентрации Р 1 и Р 2 малы и различаются мало (обе составляют приблизительно 0.2 вес. %), плотности r1 и r2 практически равны, так что с хорошей точностью можно принять n1/n2 = Р 1/ Р 2. Таким образом, уравнение (4) преобразуется к следующему
(4а)
Выпишем теперь то, что "дано", в принятых символах отдельно (см. слева), из чего видно, что можно приступать к вычислениям. Но прежде чем вычислять, подставим в правую часть уравнения (4а) единицы измерения соответствующих величин (учитывая, конечно, что логарифм и число p не имеют размерности):
Отсюда следует, что эффективная масса получится в килограммах, если расстояние x перевести из сантиметров в метры, а минуты (в числе оборотов n) перевести в секунды:
n = 6920 мин–1 = 6920 (60 с)–1 = 6920×60–1 с–1 = 6920/60 с–1 = 115.3 с–1
Таким образом:
= 
= 4.241·10–23 кг.
Из уравнений (2) и (3) теперь получаем:
кг,
кг/моль.
Заметим в заключении, что определение молярной массы по двум результатам измерений концентраций (на двух расстояниях x) в данной задаче является не очень надёжным из-за экспериментальных ошибок измерений. Фактически, в реальных исследованиях методом равновесного центрифугирования обычно определяют зависимость концентрации полимера от x, то есть получают несколько значений концентрации при разных x. В этом случае, обычный ход решения заключается в том, что строят график зависимости логарифма концентрации от x 2. Как видно из теоретического уравнения (1), такой график должен быть линейным и должен иметь коэффициент наклона равный m эффw2/(2 k B T). Определив этот коэффициент обычным графическим методом (или вычислительным методом МНК – см. приложение 5), можно найти из него эффективную массу m эфф и далее молярную массу по уравнениям (2) и (3).
Ответ: молярная масса серум глобулина М = 1.02×105 г/моль
Пример 4. (Тема: равновесие седиментации в гравитационном поле) Из кубической ёмкости размером 1×1×1 м3, заполненной жидкостью, взята проба с глубины 10 см. При её исследовании найдено присутствие двух компонент белкового вещества. Молярная масса одного 2×103 кг/моль (концентрация 0.2 г/м3) и второго 1×102 кг/моль (концентрация 0.1 г/м3). Удельный объём в растворе 0.8×103 кг/м3 у обоих компонент. Вычислите массу каждого из компонент в ёмкости и их валовые концентрации в предположении равновесия при 20 °С (плотность жидкости 1000 кг/м3). Изобразите графически распределение концентрации каждого из компонент по высоте ёмкости.
Решение. В условии задачи имеется в виду, что из-за гравитационного поля Земли распределение концентрации растворённого вещества по высоте ёмкости может быть существенно неоднородным. Согласно закону Больцмана, концентрация частиц, подверженных тепловому движению в поле тяжести, распределена по высоте экспоненциально:
c = 
(1)
где h – высота, m eff – эффективная масса частицы. Если бы распределение было однородным, то масса каждого из компонент могла бы быть найдена умножением концентрации на объём жидкости, m = c × V. Однако из-за поля тяжести концентрация на глубине 10 см может быть меньше, чем концентрация на большей глубине, и больше, чем у поверхности. Поэтому удобно начать решение задачи с построения графика, чтобы установить, действительно ли распределение белковых компонент по высоте неоднородно.
Поскольку в условии даны концентрации на глубине 0.1 м от поверхности, то разумно принять этот уровень за нулевой. То есть, у первого компонента на нулевом уровне с 01 = 0.2 г/м3, а у второго компонента с 02 = 0.1 г/м3. Поверхность жидкости будет находиться при h = +0.1 м, а дно ёмкости при h = –0.9 м. Чтобы построить графики распределения нужно вычислить несколько значений с в интервале h от –0.9 до +0.1 м.
Начнём с вычисления эффективной массы, то есть массы молекулы белкового вещества, исправленной на массу растворителя, вытесняемого объёмом молекулы. Для каждого из компонент, масса молекулы (масса в вакууме) равна m = M / N A, где М – масса одного моля (молярная масса), N A - число молекул в 1 моле вещества. Объём одной молекулы равен произведению массы молекулы на удельный объём, m × V уд. Тогда масса растворителя, вытесняемого одной молекулой, равна r mV уд. Таким образом, m eff = m – r mV уд = m (1 – r V уд) = M (1 – r V уд)/ N A. Теперь, введём обозначение для показателя степени в уравнении (1) m eff g / k B T = а. То есть,
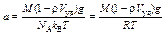(2)
потому что N A k B = R (см. приложение 2). Для двух компонент получим
= 1.61 м–1
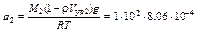= 0.0805 м–1
так как по условию V уд1 = V уд2. Подставляя значения а и с 0 в уравнение (1) получим:
c 1 = c 01exp(– a 1 h) = 0.2×exp(–1.61 h) (3)
c 2 = c 02exp(– a 2 h) = 0.1×exp(–0.0805 h) (4)
В таблице ниже приведены результаты вычислений по этим уравнениям, а на рисунке – графики, построенные по данным таблицы в общих координатных осях.
| h, м | -0.9 | -0.8 | -0.7 | -0.6 | -0.5 | -0.4 | -0.3 | -0.2 | -0.1 | 0.1 | |
| c 1,г/м3 | 0.851 | 0.724 | 0.617 | 0.525 | 0.447 | 0.380 | 0.324 | 0.276 | 0.235 | 0.200 | 0.170 |
| c 2, г/м3 | 0.108 | 0.107 | 0.106 | 0.105 | 0.104 | 0.103 | 0.102 | 0.102 | 0.101 | 0.100 | 0.099 |
Из этих результатов видно, что концентрация более лёгкого компонента (М 2 = 1×102 кг/моль) распределена почти однородно вдоль высоты. Поэтому с хорошей точностью можно принять для массы этого компонента в ёмкости m 2 = c 02× V = 0.1×1 = 0.1 г (объём всей ёмкости равен 1 м3). Концентрация более тяжелого компонента (М 1 = 2×103 кг/моль) существенно меняется с изменением глубины, из-за чего массу этого компонента нельзя вычислять по уравнению m 1 = c 01× V.
|
Поскольку концентрация первого компонента сильно зависит от h,следует рассмотреть массу растворённого вещества в малом объёме жидкости d m = c ×d V и проинтегрировать её по всему объёму. Так как переменной величиной является высота, объём следует представить как V = S × h, где S – площадь поперечного сечения. Поскольку, далее, S не зависит от h в ёмкости кубической формы, то можно записать d m = c ×d V = c d(S×h) = cS d h. С учётом (1) получим уравнение d m = S × c 0exp(– ah)d h. Таким образом,
m = 
Здесь S и с 0 вынесены из подынтегрального выражения, так как они не зависят от h. Из таблиц интегралов и правил интегрирования можно узнать, что первообразная от функции ехр(ах) равна а –1×ехр(ах). Поэтому
= 0.423 г
= 0.103 г
Из последнего результата видно, что вычисление без учёта распределения Больцмана по формуле m 2 = c 02× V = 0.100 г содержит небольшую погрешность.
Валовые концентрации находятся делением массы m на общий объём жидкости. Поскольку по условию он равен 1 м3, то валовые концентрации равны 0.423 г/м3 и 0.103 г/м3.
Ответ: m 1 = 0.423 г, с 1(валовая) = 0.423 г/м3,
m 2 = 0.103 г, с 2(валовая) = 0.103 г/м3.
Пример 5. (Тема: скорость седиментации в центрифуге) Белок овальбумин (яичный альбумин) был изучен в разбавленном водном растворе методом седиментации в ультрацентрифуге при 20 °С и числе оборотов ротора центрифуги 800 с–1 со следующими результатами:
| t, с | |||||
| x, см | 6.242 | 6.311 | 6.413 | 6.490 | 6.590 |
где х – расстояние границы мутной и прозрачной частей раствора от оси вращения ротора центрифуги.
Из дополнительных экспериментов известно, что коэффициент диффузии белка равен 7.8×10–11 м2/с, удельный парциальный объём 0.752 см3/г, плотность растворителя 0.9989 г/см3. Определите по этим данным 1) коэффициент седиментации и молярную массу белка, 2) коэффициент трения эквивалентной сферы по уравнению Стокса f 0 и истинный коэффициент трения f, 3) скорость седиментации на расстоянии х = 6.590 см и время, за которое белок пройдет путь от х 1 = 6.242 до х 2 =6.590 см, при числе оборотов 1000 с–1.
Решение. По определению, константой седиментации называется
(1)
|
где х – расстояние от оси вращения ротора центрифуги, t – время центрифугирования с угловой скоростью w. Поскольку d x / x = dln x, это уравнение можно переписать в виде s w2 = dln x /d t. Константа седиментации не зависит от расстояния х, поэтому уравнение можно проинтегрировать с результатом ln x = ln x 0 + s w2 t, где x 0 – расстояние от оси вращения в нулевой момент времени. Последнее уравнение является линейным с угловым коэффициентом s w2, в который входит искомая величина s. Таким образом, следует прологарифмировать величины х в таблице и построить график в координатах (t, ln x) (см. рисунок). Из него следует s w2 = 9.10×10–6 с–1 и s = 9.10×10–6/w2. В условии задачи угловая скорость не дана, но дано число оборотов в секунду n = 800 c–1, которое связано с угловой скоростью по известному уравнению w = 2p n. Таким образом:
с единицами измерения с–1/(с–1)2 = с.
Для определения молярной массы белка воспользуемся уравнением Сведберга
= 
= 45
с единицами измерения:
= 
.
В этом выводе было принято во внимание, что Дж = кг×м2/с2 (см. приложение 1)
Коэффициент трения белка можно найти из известного уравнения Эйнштейна D = k B T / f:
5.2×10–11 кг/с.
Если бы молекула белка была шарообразной, имела компактное внутреннее строение и не была гидратирована в растворе, то такой же коэффициент трения получился бы из известного уравнения f 0 = 6ph r. Чтобы проверить, совпадает ли f 0 c f, нужно вычислить радиус эквивалентной сферы, то есть радиус шарика, имеющего массу, равную массе молекулы белка, и тот же удельный объём. Масса одной молекулы равна М / N A, где N A – число молекул в 1 моле (число Авогадро). С другой стороны, масса 1 молекулы равна произведению её объёма на плотность. Предполагая, что молекула является сферической с радиусом r (радиус эквивалентной сферы) и плотностью r равной 1/ V уд (V уд – удельный объём), массу можно выразить
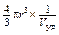. Приравнивая эти два выражения для массы одной молекулы, можно найти радиус:
= 
2.4×10–7
с единицами измерения 
= см.
Теперь можно вычислить коэффициент трения по уравнению Стокса. Хотя вязкость растворителя в условии не дана, мы можем принять её равной вязкости воды при указанной в условии температуре (1.002×10–3 Па×с). Таким образом,
f 0 = 6ph r = 6p×1.002×10–3×2.4×10–9 = 4.5×10–11 кг/с
Отношение f / f 0 = 5.2×10–11/4.5×10–11 = 1.2 показывает, что реальный коэффициент трения больше того, который молекула имела бы, если бы она была просто твёрдым шариком. Это обычная ситуация для глобулярных белков, действительная форма которых – несколько сплющенный эллипсоид вращения, а не шар. Кроме того, альбумины (глобулярные белки, хорошо растворимые в воде) слегка сольватированы в растворе, из-за чего их гидродинамический радиус (эффективный радиус в растворе) ещё больше, чем радиус "сухой" эквивалентной сферы.
Наконец, для вычисления скорости седиментации d x /d t при определённом х (х = 6.590 см) и времени седиментации между х 2 и х 1 (6.590 и 6.242 см) при другом числе оборотов, 1000 с–1, удобно воспользоваться определением константы седиментации (уравнение 1). Из него следует:
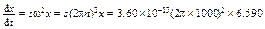= 9.36×10–5 см/с
Из него так же следует d x / x = sw2d t. Поэтому
; 
; 
;
= 3.82 ×103 с.
Заметим, что то же расстояние при числе оборотов 800 с–1 было пройдено белком за 6000 с (см. исходные данные), а при числе оборотов 1000 с–1 всего за 3820 с. Такая большая разница объясняется тем, скорость седиментации пропорциональна квадрату угловой скорости.
Ответ: 1) s = 3.60×10–13 c; M = 45×103 г/моль
Дата добавления: 2015-12-18; просмотров: 84; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!