Приложение 5. Определение коэффициентов функциональной зависимости 1 страница
Многие задачи физической и коллоидной химии формулируются приблизительно так: Даны пары чисел (xi, yi), обычно в виде таблицы
| x | x 1 | x 2 | ………. | xN |
| y | y 1 | y 2 | ………. | yN |
Требуется определить коэффициенты уравнения y = a + bx, которое, как предполагается, лежит в основе попарного соответствия чисел xi и yi.
Если бы число пар (xi, yi) было равно двум, то коэффициенты находились бы решением системы уравнений
y 1 = a + bx 1
y 2 = a + bx 2
Как известно, решением такой системы относительно a и b является:
; 
или a = y 1 – bx 1 или a = y 2 – bx 2 (1)
Однако в большинстве задач число данных пар (xi, yi) превышает 2. Если бы данные числа были точными, то можно было бы выбрать любые две пары (xi, yi), составить из них систему уравнений и решить её относительно a и b. Такое решение было бы общим и единственным для всей таблицы. В реальных задачах, однако, числа (xi, yi) содержат погрешности измерений или округлений. Поэтому для нахождения a и b применяются другие способы.
Графический способ заключается в том, что на координатную плоскость наносят точки (xi, yi) и подбирают к ним график (прямую линию) так, чтобы отклонение точек от него было, в целом, минимальным. Выбирают затем любые две точки, принадлежащие графику, определяют их координаты (x 1, y 1) и (x 2, y 2) и вычисляют a и b по уравнениям (1). Полученный коэффициент b называют угловым коэффициентом (или коэффициентом наклона), а а – начальной ординатой графика или свободным членом линейного уравнения.
|
|
|
Более точные значения a и b можно получить вычислитьльным методом наименьших квадратов (общепринятое сокращение МНК). Согласно этому методу, a и b должны быть такими, чтобы сумма квадратов отклонений
была минимальной. Из этого условия следует:
, 
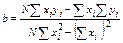(2)
где N – число пар (xi, yi).
Эти два метода применимы непосредственно только к линейным зависимостям. Однако большинство теоретических уравнений физической и коллоидной химии являются нелинейными и могут содержать, в зависимости от конкретной задачи, один или более неизвестных коэффициентов, которые требуется определить.
Если теоретическое уравнение, лежащее в основе данных пар чисел (Xi, Yi), является нелинейным вида Y = ¦(Х, A, B), то описанные выше методы можно применить после преобразования этого уравнения в линейное уравнение с новыми переменными y = a + bx, в котором х и у – функции Х и Y и любых известных параметров, но не искомых А и В, а a и b – функции искомых А и В и любых известных параметров, но не переменных Х и Y. Эта процедура называется линеаризацией функции. Вычислив новые переменные xi, yi , их обрабатывают графическим или вычислитьльным методом, как описано выше, и из полученных коэффициентов a и b находят искомые А и В.
|
|
|
Рассмотрим в качестве примера следующую задачу.
Определить коэффициенты G ¥ и K L уравнения Лэнгмюра:
(3)
для адсорбции н-гептилового спирта из водного раствора на поверхности раздела раствор/воздух по следующим экспериментальным данным
| С, ммоль/л | 0.40 | 1.00 | 2.01 | 2.80 | 3.515 | 4.81 |
| G ×103, ммоль/м2 | 1.65 | 3.00 | 4.46 | 4.54 | 5.27 | 5.63 |
Если данные пары (С i, G i) нанести на координатную плоскость, то можно видеть (рис. 5.1), что точки ложатся приблизительно так, как ожидается для теоретического уравнения (3). Можно было бы построить график, то есть подогнать к этим точкам теоретическую кривую. Однако определить искомые коэффициенты при этом трудно или почти невозможно, потому что функция (3) является нелиней-
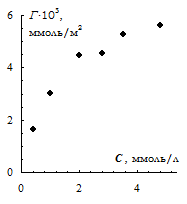ной. Поэтому уравнение (3) следует прео-бразовать в линейное с новыми перемен-ными, и применить методы определения коэффициентов, описанные выше. Возмож-ны, например, следующие способы линеа-ризации.
1) Умножим обе части уравнения (3) на знаменатель дроби в правой части (3):
G + GK L C = G ¥ K L C
и поделим обе части на K L C:
(G / K L C) + G = G ¥
Отсюда следует линейное уравнение:
G = G ¥ – 
(4-1)
вида y = a + bx с y = G, x = G / C, a = G ¥, b = –1/ K L. То есть, если вычислить G / C по числовым данным в таблице и построить график в координатах (G / C, G), то он окажется линейным и из него можно найти коэффициенты G ¥ и –1/ K L.
|
|
|
2) Возьмем обратные величины от обоих частей уравнения (3):
(4-2)
Получилось другое уравнение вида y = a + bx, с y = 1/ G, x = 1/ C, a = 1/ G ¥, b = 1/(G ¥ K L).
3) Умножим обе части уравнения (4-2) на С:
(4-3)
В этом линейном уравнении y = С / G, x = C, b = 1/ G ¥, a = 1/(G ¥ K L).
Любое из этих преобразований можно использовать для нахождения искомых коэффициентов. Рассмотрим более подробно, в качестве примера, преобразование (4-2). В отдельной таблице (табл. 5.1) перепишем исходные данные (столбцы 1 и 2) и вычислим их обратные величины (столбцы 3 и 4). Построим график в координатах (G –1, С –1), как показано на рис. 5.2. Выберем две произвольные точки, принадлежащие графику, например точку 1 с абсциссой С –1 = 0 л/ммоль и точку 2 с абсциссой С –1 = 2 л/ммоль (рис. 5.3). Определим их ординаты по соответствующей оси: G –1 = 142 м2/ммоль в точке 1 и G –1 = 513 м2/ммоль в точке 2. Таким образом, х 1 = 0, у 1 = 142, х 2 = 2, у 2 = 513, с соответствующими единицами измерения. По уравнению (1) находим угловой коэффициент b:
= 
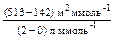= 186 м2/л
и начальную ординату: a = y 1 – b · x 1 = 142 – 186×0 = 142 м2/ммоль.
Так как a = 1/ G ¥ и b = 1/(G ¥ K L) в преобразовании (4-2), из этих результатов следует:
|
|
|
G ¥ = 1/ a = 1/142 = 7.04 ×10–3 ммоль/м2
 |
K L = 1/(G ¥ b) = 1/(7.04 ×10–3×186) = 1.31 л/ммоль
Рассмотрим решение этой же задачи методом наименьших квадратов. Чтобы найти коэффициенты по уравнениям (2), вычислим суммы S х и S у по столбцам 3 и 4 в таблице и запишем их в последней строке. Вычислим в столбцах 5 и 6 произведения ху и квадраты х 2 и так же найдем суммы в последней строке. Заметим, что число пар (xi, yi) в таблице равно 6, то есть N = 6. По уравнению (2) вычислим угловой коэффициент b:
= 
= 186 м2/л
и свободный член а:
= 
= 142 м2/ммоль.
Таблица 5.1
| С, ммоль/л | G ×103, ммоль/м2 | х = С –1, л/ммоль | у = G –1, м2/ммоль | xy | x 2 |
| 0.40 | 1.65 | 2.500 | 1512.5 | 6.250 | |
| 1.00 | 3.00 | 1.000 | 332.8 | 1.000 | |
| 2.01 | 4.46 | 0.498 | 111.6 | 0.248 | |
| 2.80 | 4.54 | 0.357 | 78.7 | 0.128 | |
| 3.515 | 5.27 | 0.284 | 54.0 | 0.081 | |
| 4.81 | 5.63 | 0.208 | 37.0 | 0.043 | |
| S = 4.847 | S = 1750 | S = 2125.9 | S = 7.749 |
Очевидно, эти результаты совпадают с теми, что были получены графическим методом, однако они, в принципе, более точны, так как построение графика "по точкам" даёт надёжные результаты только тогда, когда точки "хорошо ложатся" на прямую линию.
Следует заметить, что многие современные калькуляторы имеют встроенную программу вычислений методом наименьших квадратов, что делает применение этого метода рутинным. Однако, чтобы воспользоваться программой, необходимо внимательно изучить инструкцию к данному калькулятору.
Приложение 6. Графическое дифференцирование
Производная функции у = ¦(х) определяется как отношение изменения функции D у к изменению аргумента D х, вызывающему данное изменение D у, при том что D х стремится к нулю:
(Заметим, что d y /d x – это отношение двух бесконечно малых величин d y и d x, которые могут рассматриваться по отдельности с тем лишь ограничением, что они связаны между собой функционально, то есть не являются независимыми).
Если у = ¦(х) задана аналитически, то производная может быть найдена также аналитически, с помощью математических формул. Если функция задана численно, в виде таблицы или графика, то для нахождения производной необходимо применение других методов. Ниже рассматривается графическое дифференцирование.
Предположим, дан график линейной функции вида у = m + b × x. Выберем произвольную точку а на графике (рис. 6.1), координаты которой обозначим (х, у). Дадим абсциссе приращение D х 1. Новая точка а' будет иметь координаты (х + D х 1, у + D у 1), где приращение D у 1 определено тем, что при абсциссе х + D х 1 точка а' должна принадлежать рассматриваемому графику. Выберем новое, меньшее по величине, приращение D х 2. Соответствующая точка а'' будет иметь координаты (х + D х 2, у + D у 2). Из геометрического рассмотрения прямоугольных треугольников с катетами D х 1 и D у 1 (у одного треугольника) и D х 2 и D у 2 (у другого) ясно, что отношения D у 1/D х 1 и D у 2/D х 2 равны, потому что треугольники подобны. Очевидно, если задавать любые другие, как угодно малые приращения D х, то соответствующие отношения D у /D х будут также равны. Отсюда следует, что в случае линейной функции предел отношения D у /D х при D х, стремящемся к нулю, равен отношению D у /D х при любом D х. То есть, 
, где D х – любое, в пределах области определения функции.
Если обозначить х + D х = x' и у + D у = у', то станет ясно, что отношение D у /D х равно отношению разностей координат двух точек графика
Как упоминалось в приложении 5, это отношение равно угловому коэффициенту линейной зависимости, b.
Эти выводы находятся в точном соответствии с аналитическим определением производной функции у = m + b × x, так как
= b
Таким образом, чтобы найти производную в любой точке линейного графика, нужно определить угловой коэффициент графика. Задача графического определения этого коэффициента рассматривалась в приложении 5.
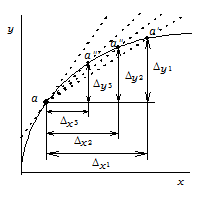Рассмотрим теперь график нелинейной зависимости (рис. 6.2). Выбрав некоторое приращение D х 1, получим точку а' с координатами (х + D х 1, у + D у 1). Отношение D у 1/D х 1 равно угловому коэффициенту секущей, проходящей через точки а и а' (штриховая линия через точку а' на рисунке). Выбирая меньшие приращения D х 2, D х 3, и так далее, будем получать новые точки а'', а''', и т.д., у которых отношения D у 2/D х 2, D у 3/D х 3, и т.д. систематически меняются с изменением D х. Это видно из изменения наклона секущих а – а', а – а'' и а – а'''. Очевидно, что при бесконечно малом приращении D х соответствующая секущая займёт предельное положение, при котором она проходит только через одну точку графика, точку а. В этом положении она называется касательной к кривой в точке а, а её угловой коэффициент равен, по определению, производной функции (заданной графиком), и именно производной в точке а.
Таким образом, в случае нелинейных графиков производная в любой точке графика не равна отношению конечных приращений D у /D х. Для её нахождения необходимо построить касательную к данной точке и определить её угловой коэффициент.
Заметим, что графическое определение производной как углового коэффициента касательной является общим и распространяется на все дифференцируемые функции, включая линейные. В случае линейной функции (рис. 6.1), касательная к любой точке графика совпадает с графиком. Поэтому для нахождения производной в этом случае достаточно определить угловой коэффициент графика.
Для построения касательной к нелинейному графику используется метод прямоугольного зеркала. Зеркало (не обязательно стеклянное, оно может быть металлическим) ставят перпендикулярно к плоскости чертежа так, чтобы его отражающий край проходил через заданную точку поперёк графика. Точное положение "поперёк" подбирают так, чтобы отражение кривой в зеркале выглядело плавным (дифференцируемым) продолжением отрезка графика, лежащего перед отражающей стороной зеркала. Это положение зеркала отвечает нормали к касательной (то есть, перпендикуляру к касательной, проходящему через точку касания). Отметив на чертеже след зеркала, строят перпендикуляр к нему, который и является касательной.
Рассмотрим графическое дифференцирование на частном примере.
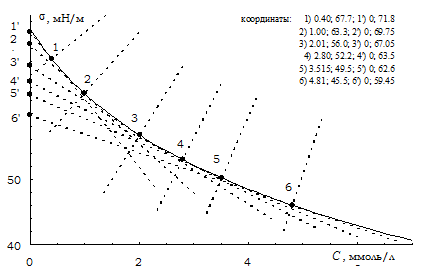
Пусть для графика зависимости поверхностного натяжения s от концентрации С, построенного в приложении 5 (рис. 5.4), требуется найти зависимость произведения - С ×ds/d C от C.
Для получения искомой зависимости необходимо определить несколько значений - С ×ds/d C при разных С. По статистическим причинам их должно быть минимум 5 или 6 во всем интервале С. Поэтому первым шагом необходимо выбрать значения абсцисс С, для которых предстоит определить значения - С ×ds/d C. На рис. 6.3 показаны подробные построения для одной из выбранных концентраций, 2 ммоль/л. Они заключаются в следующим. Отмечаем точку на графике при данной концентрации (точка 3 на рисунке). Ставим зеркало поперёк кривой так чтобы его отражающая поверхность проходила через выбранную точку, и регулируем его положение до плавного (без излома) перехода отрезка кривой, лежащего перед зеркалом, в его отражение в зеркале. Отмечаем след зеркала в этом положении (штриховая линия а–а'). Отнимаем зеркало, определяем фактические координаты точки пересечения следа зеркала с кривой и выписываем их. (Координаты точек следует записывать по мере их получения, так как по окончанию всех построений их трудно определить без ошибок из-за заграмождённости чертежа; см. рис. 6.4).
Далее следует провести линию, перпендикулярную к следу зеркала, через точку 3 до пересечения с осью ординат (линия В–В'). Проще всего это сделать с помощью чертежного треугольника. Более точный результат получается с применением циркуля (желательно кронциркуля, то есть циркуля с фиксируемым раствором). В точку пересечения следа зеркала с кривой устанавливаем ножку циркуля и, отрегулировав подходящий раствор, отмечаем дугами два равных отрезка по обоим сторонам. Устанавливаем ножку циркуля в пересечение одной из дуг со следом зеркала (например, точка А на рисунке). Увеличиваем раствор циркуля примерно в 2 раза и отмечаем две дуги приблизительно в тех местах, где должна проходить касательная к точке 3, с одной и с другой стороны от этой точки. Устанавливаем ножку циркуля в другую точку на следе зеркала (точка А'), и аналогично отчеркиваем две дуги, пересекающие первую пару дуг (точки В и В'). Если построения сделаны аккуратно, то три точки В, В' и 3 окажутся на одной прямой. Проводим прямую через эти три точки и получаем касательную.
В данной задаче, удобно провести касательную до пересечения с осью s (точка 3') и определить ординату этого пересечения. Отношение разности ординат у 3 – y 3 ' к разности абсцисс х 3 – х 3 ' равно угловому коэффициенту касательной и, поэтому, равно производной ds/d C при С = х 3. Произведение С ×ds/d C равно
так как х 3 ' = 0. Отсюда следует, что - С ×ds/d C = y 3 ' – у 3. То есть, для нахождения значения – С ×ds/d C достаточно взять разность ординаты точки 3' пересечения касательной с осью s и ординаты точки пересечения следа зеркала с графиком.
На рис. 6.4 показан окончательный график, с построенными касательными в нескольких точках кривой.
Точность графического определения производных зависит от многих условий. Одним из них является размер графика на миллиметровой бумаге. Он должен быть таким, чтобы построения для каждой касательной были совместимы с обычными размерами чертёжных инструментов. Поскольку в данном примере должно быть 5
 | |||||
| |||||
 | |||||
|
или 6 касательных, то реальный размер должен быть не менее половины стандартного формата бумаги А4. (По понятным причинам изображение на рис. 6.3 и 6.4 уменьшено). Относительные масштабы осей координат также имеют значение. Точность построения касательных уменьшается, когда в целом график построен слишком пологим (слишком сжата ось ординат) или слишком крутым (слишком сжата ось абсцисс).
Приложение 7. Примеры решения задач
Пример 1. (Тема: адсорбция на границе жидкость/газ) По экспериментальным данным о зависимости поверхностного натяжения s (мН/м) от концентрации С (ммоль/л) водных растворов н-гептилового спирта при 25.0 °С (таблица внизу) найдите предельную адсорбцию спирта G ¥ графическим методом, и вычислите площадь, занимаемую 1 молекулой спирта в насыщенном адсорбционном слое в предположении мономолекулярной адсорбции.
| С | 0.17 | 0.33 | 0.44 | 0.65 | 0.87 | 1.29 | 1.73 | 2.58 | 3.45 | 5.16 | 6.90 | |
| s | 72.1 | 71.3 | 69.8 | 69.1 | 66.1 | 64.7 | 59.2 | 58.0 | 54.2 | 50.5 | 45.1 | 40.6 |
Решение. Предельной адсорбцией G ¥ называют такую величину избыточной поверхностной концентрации рассматриваемого компонента (в данном случае гептилового спирта), которая получается экстраполяцией зависимости G от концентрации этого компонента из области низких концентраций к бесконечно большой концентрации. Иными словами, по числовым данным в условии задачи нужно найти зависимость G от С и из неё найти предел, к которому стремится G при С ® ¥. Поэтому первым шагом должно быть нахождение зависимости G = ¦(С) из зависимости s = ¦(С).
Адсорбция G связана с поверхностным натяжением двухкомпонентных растворов неэлектролитов уравнением Гиббса
(1)
Поскольку требуется графическое решение, необходимо построить график зависимости s от С (при постоянной T), и из него найти ряд значений - С ds/d C для разных С путем графического дифференцирования. Затем, зная температуру измерений, можно вычислить значения G по уравнению (1) и построить график зависимости между G и С, пригодный для графического нахождения G ¥. Свойства этой зависимости таковы, что фактически удобно строить график зависимости обратных величин, то есть G –1 от С –1. Найдя из такого графика G ¥–1, можно вычислить площадь, занимаемую одной молекулой в насыщенном мономолекулярном слое, по известному уравнению:
s m = (G ¥ N A)–1 (2)
и, разумеется, можно найти саму величину G ¥.
В этом состоит общий ход решения.
Построение графика зависимости s от С подробно обсуждается в приложении 4, а дифференцирование этого графика – в приложении 6. Результаты графического дифференцирования удобно свести в таблицу (см. ниже, столбцы 2 и 3), и продолжить вычисления в той же таблице. Делением величин - С ds/d C третьего столбца на RT = 8.315×(273.2 + 25.0) = 2.48×103 Дж/моль получаются значения G в столбце 4. Заметим, что единицы мН/м (единицы измерения С ds/d C, полученные в таблице) эквивалентны мДж/м2, потому что Дж º Н×м. Поэтому при делении С ds/d C на RT получается:
Вычислив затем G –1 и С –1 (столбцы 5 и 6), строим график (приложение 5), из которого следует G ¥–1 = 142 м2/ммоль, то есть G ¥ = 7.04×10–3 ммоль/м2 или 7.04×10–6 моль/м2. По уравнению (2) получаем:
s m = (7.04×10–6×6.022×1023)–1 = (7.04×6.022×1017)–1 = (42.395×1017)–1 = (49.395)–1×10–17 =
= 2.36×10–19
с единицами измерения:
Заметим, что уравнение Гиббса (1) может быть записано в эквивалентной форме
,
которая подсказывает другой возможный способ нахождения G: построить график в координатах ln C - s, найти коэффициенты наклона касательных к графику и вычислить G как следует из этого уравнения. Этот способ предпочтителен, когда G приходится определять из зависимости s от С в области концентраций, где адсорбция близка к насыщению мономолекулярного слоя. При таких концентрациях график ln C - s иногда оказывается линейным, так что производная ds/dln C находится просто как коэффициент наклона этого графика. Вычисленная величина G в этом случае может рассматриваться как предельная адсорбция G ¥, однако в большинстве случаев менее точная, чем полученная экстраполяцией из области низких концентраций.
Таблица вычислений в примере 1
| № точки* | С, ммоль/л |  , мН/м
| G ×103, ммоль/м2 | С –1, л/ммоль | G –1, м2/ммоль |
| 0.40 | 4.1 | 1.65 | 2.50 | ||
| 1.00 | 7.45 | 3.00 | 1.00 | ||
| 2.01 | 11.05 | 4.46 | 0.498 | ||
| 2.80 | 11.3 | 4.54 | 0.357 | ||
| 3.515 | 13.1 | 5.27 | 0.284 | ||
| 4.81 | 13.95 | 5.63 | 0.208 |
* № точки на рисунке 6.4 (приложение 6)
Дата добавления: 2015-12-18; просмотров: 63; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!