Классификация элементарных функций
К основным элементарным функциям относятся следующие функции:
− степенная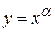 
(
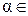R, 
;
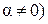− показательная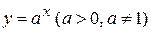 
;
− логарифмическая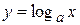 
;
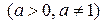− тригонометрические
;
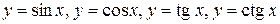− обратные тригонометрические 
;
Определение. Элементарной называется функция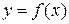 
, полученная из основных элементарных функций и функций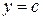 
(с – число) с помощью конечного числа арифметических операций и композиций.
Примеры. 
– элементарная функция.
Функции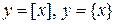 
не являются элементарными.
Определение. Многочленом п - ой степени называетсяфункция вида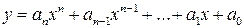 
, где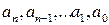 
– числа, 
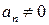, п – неотрицательное целое число.
Примеры.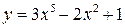 
– многочлен 5-ой степени, 
– многочлен нулевой степени
Определение. Рациональной функцией называется частное двух многочленов.
Пример.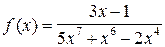 
– рациональная функция.
Многочлен является частным случаем рациональной функции.
Определение. Функция 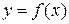называется алгебраической, если она получена из функций 
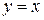и y = c (c – произвольное число) с помощью конечного числа арифметических операций, взятия корней натуральной степени и композиции функций.
Например, рациональные функции являются алгебраическими.
Определение. Алгебраическая функция 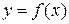, не являющаяся рациональной, называется иррациональной.
Пример.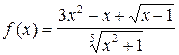 
– иррациональная функция.
Определение. Функция 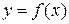, не являющаяся алгебраической, называется трансцендентной.
К трансцендентным функциям, например, относятся все тригонометрические, обратные тригонометрические, показательная и логарифмическая функции.
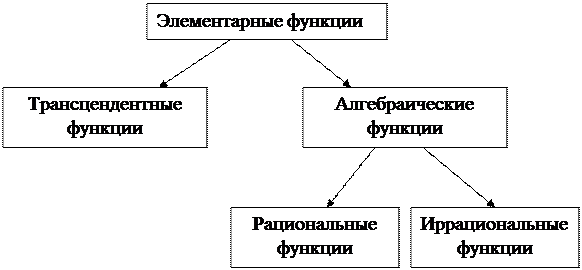
Классификацию элементарных функций можно представить следующей схемой.
Дата добавления: 2015-12-17; просмотров: 21; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!