Потенциал. Эквипотенциальные поверхности
Электростатическое поле обладает потенциальной энергией, поэтому наряду с напряженностью поля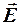 
для описания полей используется такая характеристика поля, как потенциал.
Потенциал электростатического поля φ – СФВ, являющаяся энергетической характеристикой поля и численно равная потенциальной энергии, которой обладал бы в данной точке поля единичный положительный точечный заряда:
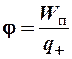(2.10)
За единицу измерения потенциала в СИ принимают 1 Вольт
[ φ ] = 1В =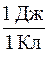 
.
Потенциал не зависит ни от потенциальной энергии W П ни от заряда q +, а является характеристикой поля.
GGG Подчеркнем, что, в отличие от напряженности, потенциал – не векторная, а скалярная величина. Он может быть как положительным, так и отрицательным. Потенциал поля, созданного положительным зарядом, положителен, а потенциал поля, созданного отрицательным зарядом, отрицателен.
Для потенциала справедлив принцип суперпозиции: потенциал поля, созданного в данной точке системой положительных и отрицательных зарядов, равен алгебраической сумме потенциалов полей, созданных каждым зарядом в отдельности с учетом их знаков:
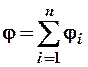. (2.11)
Численное значение потенциала зависит от выбора нулевого уровня φ.
Нулевой уровень потенциала – геометрическое место точек поля, потенциал которых принимается равным нулю и выбирается произвольно: в бесконечности, на поверхности Земли и т. д.
Потенциал поля, созданного точечным зарядом Q на расстоянии r от него:
|
|
|
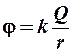. (2.12)
Для графического изображения распределения потенциала пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал φ имеет одно и то же значение.
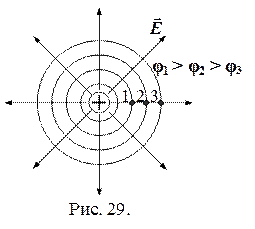
Форма эквипотенциальных поверхностей может быть разная, например, для точечного заряда эквипотенциальные поверхности – концентрические сферы (рис. 29).
Эквипотенциальных поверхностей вокруг каждого заряда можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей характеризует напряженность поля в разных точках. Чем гуще эквипотенциальные поверхности, тем больше напряженность поля.
Свойства эквипотенциальных поверхностей:
1) работа по перемещению заряда по эквипотенциальной поверхности равна нулю;
2) линии вектора напряжённости всегда перпендикулярны эквипотенциальным поверхностям;
3) эквипотенциальные поверхности не пересекаются, так как одна и та же точка поля не может иметь два разных значения потенциала;
4) густота эквипотенциальных поверхностей пропорциональна модулю потенциала, т. е. она характеризует пространственное распределение потенциала.
|
|
|
Зная расположение линий напряжённости электростатического поля, можно построить эквипотенциальные поверхности, и наоборот. Следовательно, электростатическое поле считается полностью заданным, если для каждой точки пространства задан вектор 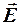или скаляр φ.
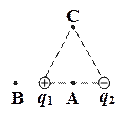1. Электрическое поле создается двумя равными по величине зарядами: + q 1 и – q 2. Укажите ошибочную запись:
а) Е А > EB; б) φ B > 0; в) φ C = 0;
г) E C ≠ 0; д) φ A< 0; е) Е А = 0.
 |
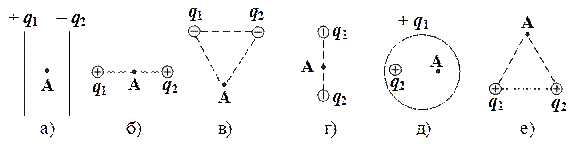2. На каком из рисунков потенциал результирующего поля в точке А равен нулю, если расстояние от зарядов до точки А одинаково (| q 1 | = | q 2 |)
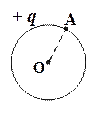3. Потенциалы в точках А и О поля, созданного положительно заряженной сферой, удовлетворяют условиям:
а) φ O = φ А> 0; б) φ O > φ A > 0; в) φ A > φ O > 0;
г) φ O < φ A < 0; д) φ O = φ А= 0; е) φ O = φ А< 0.
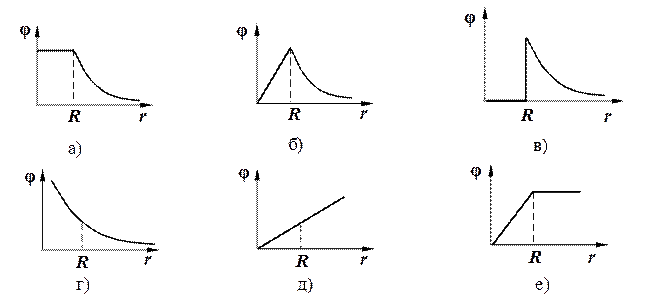
4. Найти правильный график зависимости φ (r) для положительно заряженного металлического шара радиуса R.
 |
5. В каком случае разность потенциалов между точками поля А и В равна нулю?
6. Найти ошибочную запись для эквипотенциальных поверхностей:
а) q Δφ = 0; б) φ = const; в)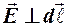 
;
|
|
|
г)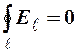 
; д)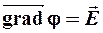 
; е) Е = const.
где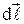 
- элемент длины эквипотенциальной поверхности.
.
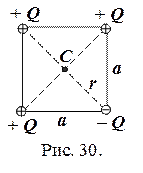
Задача 2.10. В вершинах квадрата со стороной а расположены три положительных заряда и один отрицательный. Значение каждого заряда равно Q. Определить потенциал электростатического поля в центре квадрата.
Решение. Согласно принципу суперпозиции (2.11), потенциал результирующего поля
.
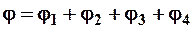GGG Внимание: при расчете потенциала знаки зарядов учитываются автоматически, поэтому значение результирующего потенциала не зависит от того, как расположены положительные и отрицательные заряды в вершинах квадрата.
Как видно из рис. 30, расстояние от любого из зарядов до рассматриваемой точки одинаково и вычисляется из теоремы Пифагора:
.
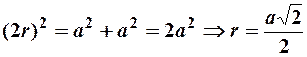Потенциал, создаваемый каждым зарядом, согласно (2.12) равен:
.
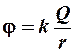Подставив в принцип суперпозиции значение потенциала и значение r, получим:
.
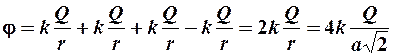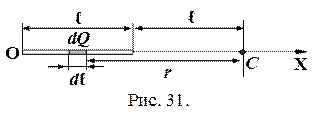Задача 2.11. Тонкий стержень длиной ℓ равномерно заряжен зарядом Q. Найти потенциал поля в точке С, расположенной на оси стержня на расстоянии, равном длине стержня от его ближайшего конца.
Решение. Разобьем стержень на элементарные участки длиной d ℓ с зарядом dQ. Каждый такой участок можно принять за точечный заряд, создающий по формуле (2.12) потенциал
|
|
|
,
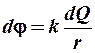где r – расстояние от элемента d ℓ до точки С;
dQ = τ d ℓ – из определения линейной плотности заряда (1.3).
Потенциал результирующего поля
,
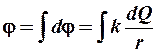где интегрирование ведется по всему заряду.
Поскольку требуется найти потенциал в точке, лежащей на оси стержня, введем ось ОХ (рис. 31). Тогда длина элемента d ℓ = dx, а расстояние от этого элемента до точки С r = х, которое изменяется от ℓ до 2 ℓ. Тогда потенциал в точке С вычисляется так:
.
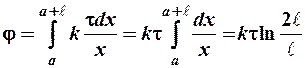С учетом того, что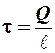 
, окончательно получим:
.
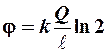Задача 2.12. Тонкий диск радиуса R равномерно заряжен с поверхностной плотностью σ. Найти потенциал поля в точке А, лежащей на оси диска на расстоянии а от него.
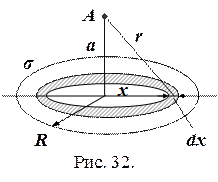Решение. Чтобы найти потенциал в точке А, надо применить принцип суперпозиции полей (2.11). Разобьем диск на элементарные кольца толщиной dх (рис. 32). Площадь кольца радиуса х
S = 2π xdx,
а заряд кольца (из формулы (1.4))
Q = σ S = 2πσ xdx.
Потенциал поля элементарного кольца равен сумме потенциалов, созданных всеми его точечными элементами. Так как эти элементы находятся на одинаковом расстоянии от точки А, то, заменив заряд кольца точечным зарядом той же величины, удаленным на расстоянии
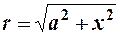
от точки А, найдем по формуле (2.12) потенциал элементарного кольца:
.
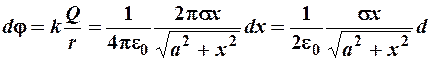Чтобы определить потенциал диска, надо проинтегрировать потенциалы элементарных колец:
.
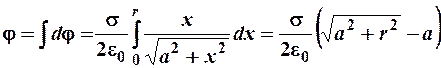Дата добавления: 2016-01-05; просмотров: 35; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!