Напряжённость электростатического поля, внутри объемно заряженного шара
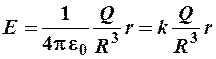(r ≤ R). (2.9)
.
Задача 2.3. В поле бесконечно длинной плоскости с поверхностной плотностью заряда σ подвешен на нити маленький шарик массой m, имеющий заряд того же знака, что и плоскость. Найти заряд шарика, если нить образует с вертикалью угол α
Решение. Вернемся к разбору решения задачи 1.4. Разница заключается в том, что в задаче 1.4 сила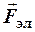 
вычисляется по закону Кулона (1.2), а в задаче 2.3 – из определения напряженности электростатического поля (2.1) 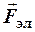. Напряженность электростатического поля бесконечной равномерно заряженной плоскости выведена с использованием теоремы Остроградского-Гаусса (2.4).
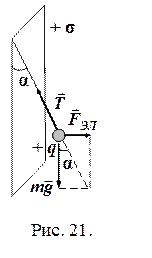Поле плоскости однородно и не зависит от расстояния до плоскости. Из рис. 21:
.
GGG Обратите внимание, что для нахождения силы, действующей на заряд, помещенный в поле распределенного заряда, необходимо использовать формулу
,
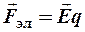а напряженность поля, созданного несколькими распределенными зарядами, находить по принципу суперпозиции. Поэтому последующие задачи посвящены нахождению напряженности электростатического поля распределенных зарядов с использованием теоремы Остроградского-Гаусса.
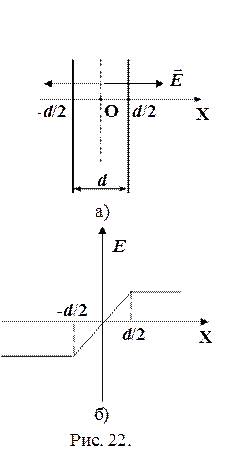
Задача 2.4. Опередить напряженность поля внутри и вне равномерно заряженной пластинки толщиной d, объемная плотность заряда внутри пластинки ρ. Построить график зависимости Е (х).
Решение. Начало координат поместим в средней плоскости пластинки, а ось ОХ направим перпендикулярно к ней (рис. 22, а). Применим теорему Остроградского-Гаусса для расчета напряженности электростатического поля заряженной бесконечной плоскости, тогда
|
|
|
.
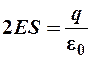Из определения объемной плотности заряда
,
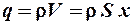тогда для напряженности получим
.
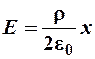Отсюда видно, что поле внутри пластинки зависит от х. Поле вне пластинки рассчитывается аналогично:
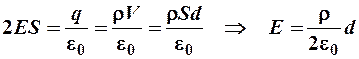
Отсюда видно, что поле вне пластинки однородно. График зависимости напряженности Е от х на рис. 22, б.
Задача 2.5. Поле создано двумя бесконечно длинными нитями, заряженными с линейными плотностями зарядов – τ1 и + τ2. Нити расположены перпендикулярно друг другу (рис. 23). Найти напряженность поля в точке, находящейся на расстоянии r 1 и r 2 от нитей.
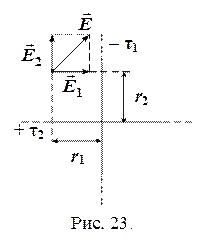Решение. Покажем на рисунке напряжённость поля, созданного каждой нитью отдельно. Вектор 
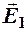направлен к первой нити, так как она заряжена отрицательно. Вектор 
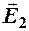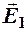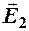направлен от второй нити, так как она заряжена положительно. Векторы и взаимно перпендикулярны, поэтому результирующий вектор 
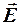будет являться гипотенузой прямоугольного треугольника. Модули векторов 
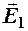и 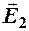определяются по формуле (2.5).
По принципу суперпозиции
.
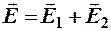По теореме Пифагора
.
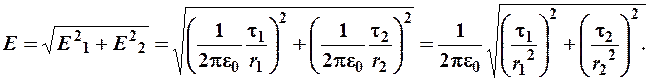Задача 2.6. Поле создано двумя заряженными бесконечно длинными полыми коаксиальными цилиндрами радиусами R 1 и R 2 > R 1. Поверхностные плотности зарядов равны – σ1 и + σ2. Найти напряжённость электростатического поля в следующих точках:
|
|
|
а) точка А расположена на расстоянии d 1 < R 1;
б) точка В расположена на расстоянии R 1 < d 2 < R 2;
в) точка С расположена на расстоянии d 3 > R 1 > R 2.
Расстояния отсчитываются от оси цилиндров.
Решение. Коаксиальные цилиндры – это цилиндры, имеющие общую ось симметрии. Сделаем рисунок и покажем на нем точки (рис. 24).
а)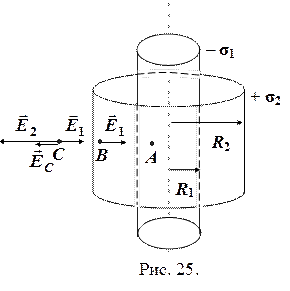 
точка А расположена внутри обоих цилиндров. Так как внутри цилиндров поля нет, то напряжённость в этой точке равна нулю:
Е А = 0.
б) точка В расположена внутри бóльшего цилиндра, поэтому в этой точке поле создаётся только меньшим цилиндром:
.
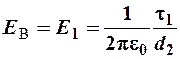Выразим линейную плотность заряда через поверхностную плотность заряда. Для этого воспользуемся формулами (1.4) и (1.5), из которых выразим заряд:
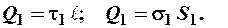
Приравняем правые части и получим:
,
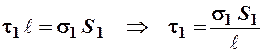где S 1 – площадь поверхности первого цилиндра.
С учётом того, что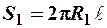 
, окончательно получим:
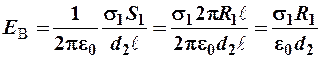
в) точка С расположена снаружи обоих цилиндров, поэтому поле создаётся обоими цилиндрами. По принципу суперпозиции:
.
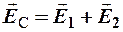С учётом направлений и расчётов, полученных выше, получим:
|
|
|
.
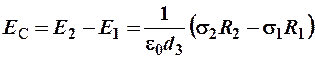Задача 2.7. Поле создано двумя заряженными бесконечно длинными параллельными плоскостями. Поверхностные плотности зарядов равны σ 1 и σ 2 > σ 1. Найти напряжённость электростатического поля в точках, находящихся между пластинами и вне пластин. Решить задачу для двух случаев:
а) пластины одноимённо заряжены;
б) пластины разноимённо заряжены.
Решение. В векторном виде напряжённость результирующего поля в любом случае записывается одинаково. Согласно принципу суперпозиции:
.
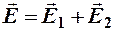Модули векторов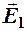 
и 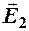вычисляются по формуле (2.6).
а) Если плоскости заряжены одноимённо, то между плоскостями напряжённости направлены в разные стороны (рис. 26, а). Модуль результирующей напряжённости
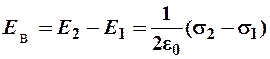
Вне плоскостей напряжённост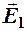и и 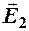направлены в одну сторону. Так как поле бесконечных заряженных плоскостей однородно, то есть не зависит от расстояния до плоскостей, то в любой точке и слева и справа от плоскостей поле будет одинаково:
. 
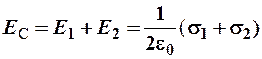
б) Если плоскости заряжены разноимённо, то, наоборот, между плоскостями напряжённости направлены в одну сторону (рис. 26, б), а вне плоскостей – в разные.
Дата добавления: 2016-01-05; просмотров: 24; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!