Упорядоченное дерево Хаффмана.

⇐ ПредыдущаяСтр 7 из 18Следующая ⇒

Бинарное дерево называется упорядоченным, если его узлы могут быть перечислены в порядке не убывания веса и в этом перечне узлы, имеющие общего родителя, должны находиться рядом, на одном ярусе. Причем перечисление должно идти по ярусам снизу-вверх и слева - направо в каждом ярусе.

На рис. 4 приведен пример упорядоченного дерева Хаффмана.

Если дерево кодирования упорядоченно, то при изменении веса существующего узла дерево не нужно целиком перестраивать - в нем достаточно лишь поменять местами два узла; узел, вес которого нарушил упорядоченность, и последний из следующих за ним узлов меньшего веса. После перемены мест узлов, необходимо пересчитать веса всех их узлов-предков.

Например, если в дереве на рис. 4 добавить еще две буквы А, то узлы А и D должны поменяться местами (см. рис. 5).

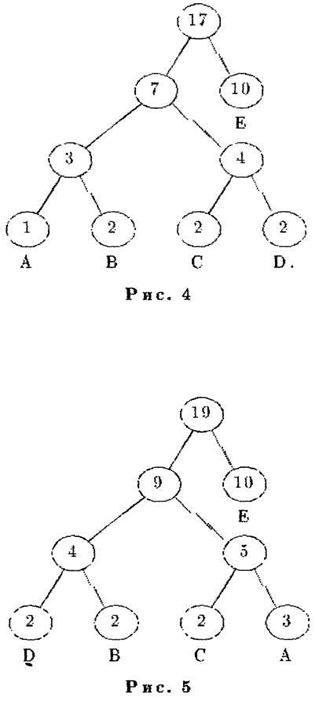
Если добавить еще две буквы А, то необходимо будет поменять местами сначала узел А и узел, родительский для узлов D и В, а затем узел Е и узел-брат Е (рис. 6).

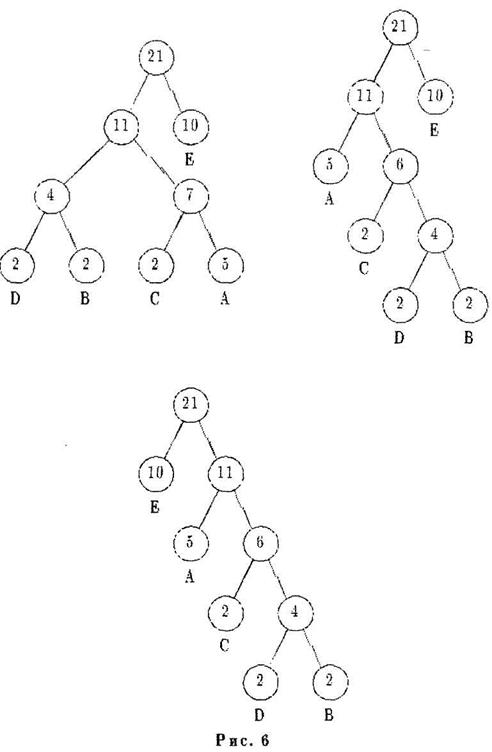
Дерево нужно перестраивать только при появлении в нем нового узла-листа. Вместо полной перестройки можно добавлять новый лист справа к листу (ESC) и упорядочивать, если необходимо, полученное таким образом дерево.

Процесс работы адаптивного алгоритма Хаффмана с упорядоченным деревом можно изобразить следующей схемой:

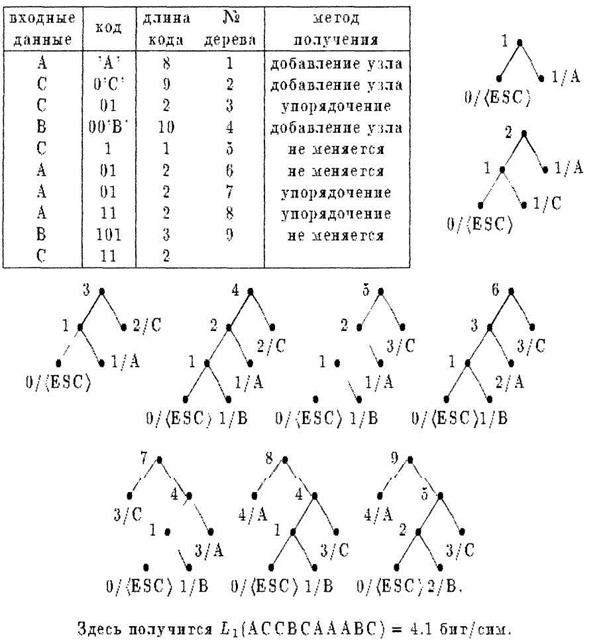
Рассмотрим еще один пример.

Сообщение

…_МАМА_ МЫЛА_ РАМУ_....

Поток данных

(00) (010) (001) (010) (001) (000) (010)

3 бит/символ =16 символов = 48 бит.

Проиллюстрируем сказанное на несколько шутливом примере кодирования текстов начальной части букваря, в которой используется лишь 6 букв (рис. 1) Для равномерного кодирования этих букв и символа пробела надо использовать комбинации из трех двоичных знаков. В этом случае для кодирования фразы из 16 символов (букв и пробелов) потребуется 48 двоичных знаков. Но расходование 3 двоичных знаков на букву не означает, что каждая двоичная комбинация переносит 3 бита информации. Если считать фразу "мама мыла раму" типичным представителем текстов начальной части букваря, то по ней можно оценить вероятности появления каждого символа (рис.2). Расчет энтропии дает значение 2,5 бит/буква. Используя код Хаффмана, можно добиться того, чтобы для кодирования одной буквы расходовалось бы в среднем 2,5 двоичных знаков.

Энтропийное кодирование

Символ	N	P_i	Код
-	4	¼	00
А	4	¼	01
М	4	¼	10
Л	1	1/16	1100
Р	1	1/16	1101
У	1	1/16	1110
Ы	1	1/16	1111

Сообщение

…_МАМА_ МЫЛА_ РАМУ_....

передаваемые данные

00 10 01 10 01 00 10 1111 1100 01 00 1101 01 10 1110 00 – 40 бит

Пример формирования кода Хаффмана приведен на рис.3. Все символы располагаются в порядке убывания их вероятностей. Два нижних, т.е. наименее вероятных символа объединяются в один, которому приписывается суммарная вероятность. Верхнему символу этого объединения ставится в соответствие (в качестве цифры кодового слова) цифра 0, нижнему - 1. Объединение занимает в новой группировке символов положение, соответствующее его общей вероятности. Два наименее вероятных символа опять объединяются по тем же правилам. Этот процесс повторяется до тех пор, пока в результате объединения не получится суммарная вероятность, равная единице. Для составления кода каждого символа надо проследить путь к этому символу от последней группировки.

(Следует иметь в виду, что значение энтропии данного примера не относится к текстам, взятым не из букваря)

Избыточность сообщений.

Но статистическая структура языка более сложна, чем это можно предполагать по данным приведенного примера. В текстах можно заметить определенные многобуквенные сочетания, отражающие корреляционные связи между буквами текстов. Например, за гласной буквой с большой вероятностью следует согласная, но никогда не следует мягкий знак (такие особенности учтены при разработке клавиатур пишущих машин и компьютеров). Если принять во внимание вероятности двухбуквенных сочетаний, то энтропия становится равной Н2 =3,5; с учетом трехбуквенных сочетаний энтропия уменьшается до НЗ=3,0 бит/буква. Если ограничиться восемью буквенными сочетаниями, то можно оценить энтропию осмысленного текста как Н=Н8=2,3 бит/буква.

Величиной R=1-(H/HO) принято характеризовать избыточность сообщения. Коэффициент R принимает значения в диапазоне от 0 до 1. Он равен 0 (избыточность отсутствует), если Н=Н₀. Это может быть в случае, если все символы алфавита независимы и равновероятны. Энтропия Н при этом принимает максимально возможное значение НО. Каждый символ сообщения переносит Н₀ битов информации, каждый разряд равномерного двоичного кода, описывающего сообщение, - 1 бит, что и соответствует сообщению без избыточности. Коэффициент R стремится к 1 (или 100%), если Н « Н₀ , что означает малую информативность и высокую степень предсказуемости текста данного сообщения.

Это может быть в случае, если символы алфавита характеризуются значительно отличающимися вероятностями появления в текстах сообщений, например, когда один символ алфавита значительно более вероятен, чем другие. Это может быть также и при близких вероятностях появления отдельных символов, если в текстах сообщений можно обнаружить сильные корреляционные связи, проявляющиеся в частом повторении определенных многобуквенных сочетаний. Данное обстоятельство и допускает возможность предсказания не принятого еще текста сообщения (или хотя бы его фрагмента) на основе уже полученной части сообщения. Как видно, коэффициент R показывает, на какой процент может сократиться длина сообщения, если применить экономное кодирование.

Сообщение из N букв содержит Н*N информации. При двоичном кодировании его длина составит H₀*N двоичных знаков. Экономное кодирование, учитывающее вероятности появления букв и сочетаний, позволяет в принципе сократить длину сообщения до H*N двоичных знаков. Величину CR=(H₀*N)/(H*N)= (log2M)/H можно назвать максимально возможным коэффициентом компрессии.

Следует иметь в виду, что, определяя количество информации в сообщениях и оценивая их избыточность, мы учитываем только статистику появления отдельных символов алфавита и их сочетаний и не затрагиваем семантические и прагматические аспекты информации.

Как следует из приведенных выше рассуждений, избыточность текста на русском языке превышает 50%. Избыточность других распространенных европейских языков также велика. Однако это часто доказывается полезным. Именно избыточность языка позволяет понимать речь иностранца, говорящего с акцентом и ошибками, редактировать текст при наличии опечаток, а также восстанавливать исходное сообщение в случае пропусков целых слов (вспомните записку капитана Гранта).

Код Фано.

Кодирование всех сообщений словами одинаковой длины, что, однако, далеко не всегда бывает выгодно.

Представим себе, что одни сообщения приходится передавать довольно часто, другие — редко, третьи — совсем в исключительных случаях. Понятно, что первые лучше закодировать тогда короткими словами, оставив более длинные слова для кодирования сообщений, появляющихся реже. В результате кодовый текст станет в среднем короче, и на его передачу потребуется меньше времени.

Впервые эта простая идея была реализована упоминавшимся нами американским инженером Морзе в предложенном им коде. Рассказывают, что создавая свой код, Морзе отправился в ближайшую типографию и подсчитал число литер в наборных кассах. Буквам и знакам, для которых литер в этих кассах было припасено больше, он сопоставив более короткие кодовые обозначения (ведь эти буквы встречаются чаще). Так, например, в русском варианте азбуки Морзе буква «е» передается одной точкой, а редко встречающаяся буква «ц» — набором из четырех символов

В математике мерой частоты появления того или иного события является его вероятность. Вероятность события А обозначают обычно символом Р(А) или просто буквой Р. Не останавливаясь на определении вероятности, заметим только, что вероятность некоторого события (сообщения) можно представлять себе как долю тех случаев, в которых оно появляется,, от общего числа появившихся событий (сообщений).

Так, если заданы четыре сообщения A 1, А2, А3, А4 с вероятностями P ( A 1)=1/2, Р(Аг)=1/4, Р(Аз)=Р(А₄)= 1/8, то это означает, что среди, например, 1 000 переданных сообщений около 500 раз появляется сообщение А1 около 250 — сообщение А2 и примерно по 125 раз — каждое из сообщений A 3 и А 4

Эти сообщения нетрудно закодировать двоичными словами длины 2, например так, как показано в следующей таблице

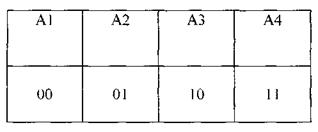
Однако при таком кодировании вероятность появления сообщений никак не учитывается. Поступим теперь иначе, разобьем сообщения на две равновероятные группы в первую попадает сообщение А1, во вторую - сообщения А2, Аз, А 4., Сопоставим первой группе символ 0, второй — символ 1 (см таблицу, во второй графе таблицы указаны вероятности сообщений).

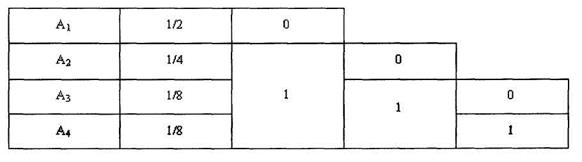
Это вполне в духе принципа, применявшегося в задаче с угадыванием Действительно, символ 0 соответствует ответу «да» на вопрос «принадлежит ли сообщение первой группе ?», а 1 — ответу «нет» Разница лишь в том, что раньше все множество разбивалось на две группы с одинаковым числом элементов, теперь же в первой группе один, а во второй — три элемента. Но, как и раньше, разбиение это таково,- что оба ответа «да» и «нет» равновозможны. Продолжая в том же духе, разобьем множество сообщений А2, A3, A 4, снова на две равновероятные группы. Первой, состоящей из одного сообщения А2, сопоставим символ 0, а второй, в которую входят сообщения Аз и А4,— символ 1. Наконец оставшуюся группу из двух сообщений разобьем на две группы, содержащие соответственно сообщения А3 и А4, сопоставив первой из них 0, а второй — символ 1. Сообщение A 2 образовало «самостоятельную» группу на первом шаге, ему был сопоставлен символ 0, слово 0 и будем считать кодом этого сообщения. Сообщение А2 образовало самостоятельную группу за два шага, на первом шаге ему сопоставлялся символ 1, на втором - 0, поэтому будем кодировать сообщение A 2 словом 10. Аналогично, для Аз и А4 выбираем соответственно коды 110 и 111. В итоге получается следующая кодовая таблица

Указанный здесь способ кодирования был предложен американским математиком Фано. Оценим тот выигрыш который дает в нашем случае код Фано по сравнению с равномерным кодом, когда все сообщения кодируются словами длины 2. Представим себе, что нужно передать в общей сложности 1000 сообщений При использовании равномерного кода на их передачу потребуется 2000 двоичных символов.

Пусть теперь используется код Фано. Вспомним, что из 1000 сообщений примерно 500 раз появляется сообщение A 1 которое кодируется всего одним символом (на это уйдет 500 символов), 250 раз- сообщение А2, кодируемое двумя символами (еще 500 символов), примерно по 125 раз -сообщения Аз и А₄ с кодами длины 3 (еще 3 X 125+3 X 125= 750 символов). Всего придется передать примерно 1750 символов. В итоге мы экономим восьмую часть того времени, которое требуется для передачи сообщений равномерным кодом. В других случаях экономия от применения кода Фано может оказаться еще значительнее.

Уже этот пример показывает, что показателем экономности или эффективности

неравномерного кода являются не длины отдельных кодовых слов, а «средняя» их длина ĺ определяемая равенством.

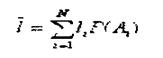
где l_i - длина кодового обозначения для сообщения A_i, P ( Ai ) — вероятность сообщения A_i, N- общее число сообщений.

Наиболее экономным оказывается код с наименьшей средней длиной ĺ . В примере для кода Фано.

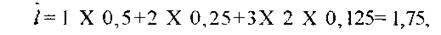
в то время как для равномерного кода средняя длина ĺ =2 (она совпадает с общей длиной кодовых слов).

Нетрудно описать общую схему метода Фано. Располагаем N сообщений в порядке убывания их вероятностей: Р(А1)?Р(А2)?... ?Р(А_N). Далее разбиваем множество сообщений на две группы так, чтобы суммарные вероятности сообщений каждой из групп были как можно более близки друг к другу. Сообщениям из одной группы в качестве первого символа кодового слова приписывается символ 0, сообщениям из другой - символ 1. По тому же принципу каждая из полученных групп снова разбивается на две части, и это разбиение определяет значение второго символа кодового слова. Процедура продолжается до тех пор, пока все множество не будет разбито на отдельные сообщения. В результате каждому из сообщений будет сопоставлено кодовое слово из нулей и единиц.

Понятно, что чем более вероятно сообщение, тем быстрее оно образует «самостоятельную» группу и тем более коротким словом оно будет закодировано. Это обстоятельство и обеспечивает высокую экономность кода Фано.

Описанный метод кодирования можно применять и в случае произвольного алфавита из d символов с той лишь разницей, что на каждом шаге следует производить разбиение на d равновероятных групп.

Дата добавления: 2022-01-22; просмотров: 257; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!