Способы измерения информации.
Понятие количества информации естественно возникает, например, в следующих типовых случаях:
1. Равенство вещественных переменных а = b . заключает в себе информацию о том, что а равно b . Про равенство а2 = b 2 можно сказать, что оно несет меньшую информацию, чем первое, т.к. из первого следует второе, но не наоборот. Равенство а3 = b 3 несет в себе информацию по объему такую же, как и первое;
2. Пусть происходят некоторые измерения с некоторой погрешностью. Тогда чем больше будет проведено измерений, тем больше информации об измеряемой сущности будет получено;
3. Матем. ожид.некоторой случ. велич. содержит в себе информацию о самой случ. велич. Для случ. велич., распределенной по нормальному закону, с известной дисперсией знание матем. ожид. дает полную информацию о случ. велич.;
4. Рассмотрим схему передачи информации. Пусть передатчик описывается случ. велич. Х, тогда из - за помех в канале связи на приемник будет приходить случ. велич. Y = X + Z . где Z это случ. велич. описывающая помехи. В этой схеме можно говорить о количестве информации, содержащейся в случ. велич. Y относительно Х. Чем ниже уровень помех (дисперсия Z мала), тем больше информации можно получить из Y. При отсутствии помех Y содержит в себе всю информацию об X .
В 1865 г. немецкий физик Рудольф Клаузиус ввел в статистическую физику понятие энтропии или меры уравновешенности системы.
В 1921 г. основатель большей части математической статистики, англичанин Роналд Фишер впервые ввел термин "информация" в математику, но полученные им формулы носят очень специальный характер.
|
|
|
В 1948 г. Клод Шеннон в своих работах по теории связи выписывает формулы для вычисления количества информация и энтропии. Термин "энтропия" используется Шенноном по совету патриарха компьютерной эры фон Неймана, отметившего, что полученные Шенноном для теории связи формулы для ее расчета совпали с соответствующими формулами статистической физики, а также то, что "точно никто не знает" что же такое энтропия.
Лекция 3. Понятие энтропии. Семантическая информация.
Смысл энтропии Шеннона.
Энтропия д.с.в. - это минимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной д.с.в.
Рассмотрим пример (скачки). В заезде участвуют 4 лошади с равными шансами на победу, т.е. вероятность победы каждой лошади равна 1/4. Введем д.с. в. Х, равную номеру победившей лошади. Здесь НХ = 2. После каждого наезда по каналам связи достаточно будет передавать два бита информации о номере победившей лошади. Кодируем номер лошади следующим образом:
1 00, 2 01, 3 10, 4 11.
|
|
|
Если ввести функцию L ( X ), которая возвращает длину сообщения, кодирующего заданное значение X , то матем. ожид. ML ( X ) это средняя длина сообщения, кодирующего X . Можно формально определить L через две функции L ( X ) = len ( code ( X )), где code ( X ) каждому значению X ставит в соответствие некоторый битовый код, причем, взаимно однозначно, a len возвращает длину в битах для любого конкретного кода.L это функция от д.с.в., т.е. тоже д.с.в. В этом примере ML ( X ) = НХ.
Пусть теперь д.с.в. X имеет следующее распределение
Р(Х = 1) =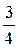 
, Р(Х = 2) = 
, Р(Х = 3) = Р(Х = 4) = 
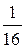
т.е. лошадь с номером 1 это фаворит. Тогда
Закодируем номера лошадей; 1 0, 2 10, 3110, 4 111, т.е. так, чтобы каждой код не был префиксом другого кода (подобное кодирование называют префиксным). В среднем в 16 заездах 1-я лошадь должна победить в 12 из них. 2-я в 2-х. 3-я в 1-м и 4-я в 1-м, Таким образом, средняя длина сообщения о победителе равна (1* 12+2* 2+3*1+3* 1) /16 = 1.375 бит/сим. или матем. ожид. L (Х). Действительно, L ( X ) сейчас задается следующим распределением вероятностей: Р( L (Х) = 1) = ¾, P ( L [ X ) = 2) = 1/8, P ( L ( X ) = 3) = 1/8.
Следовательно,
ML ( X )= 
= 1.375 бит/сим
Итак, ML ( X ) > НХ.
Можно доказать, что более эффективного кодирования для двух рассмотренных случаев не существует.
То, что энтропия Шеннона соответствует интуитивному представлению о мере информации, может быть продемонстрировано в опыте по определению среднего времени психических реакций. Опыт заключается в том, что перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия испытании, в которых каждая лампочка зажигается с определенной вероятностью 
где i -это номер лампочки. Оказывается, среднее время, необходимое для правильного ответа испытуемого, пропорционально величине энтропии - 
, а не числу лампочек N, как можно было бы подумать, В этом опыте предполагается, что чем больше информации будет получено человеком, тем дольше будет время ее обработки и, соответственно, реакции на нее.
|
|
|
Дата добавления: 2022-01-22; просмотров: 94; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!