Стационарные случайные процессы. Определение стационарности в узком и широком смысле.
Первый называется стационарным в узком смысле если плотности распределения вероятностей для них не зависят от выбора начального отсчета:
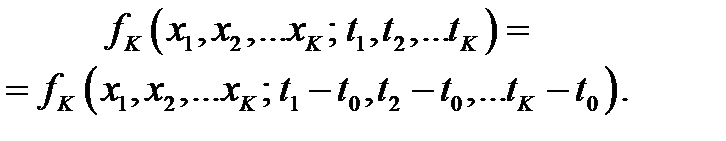
| (4.41) |
Применим свойство стационарности к математическому ожиданию:
| (4.42) |
Согласно общему определению, можно принять 
. Тогда получим, что математическое ожидание не зависит от времени, так как плотность распределения так же от него не зависит:
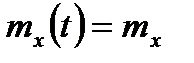
| (4.43) |
Аналогичные рассуждения справедливы и для дисперсии. Так как двумерная плотность распределения превращается в одномерную, то выражение (4.40) приобретает форму:
| (4.44) |
т. е. дисперсия не зависит от времени.
Еще одна очень полезная характеристика – центральный смешанный момент второго порядка, или корреляционная функция:
 
| (4.45) |
Согласно определению стационарности, введём в рассмотрение относительные значения времени: вместо 
и 
будем рассматривать относительные значения разностей аргументов во времени. Тогда получим, что корреляционная функция зависит от одного аргумента 
:
| (4.46) |
Мы получили функцию от одного аргумента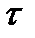 
, являющегося разностью двух моментов времени: . Эти аргумент и функция имеют основополагающее значение в теории случайных процессов. Для иллюстрации свойств корреляционной функции предположим, что 
. Тогда образуется формула вида:
| (4.47) |
Можно сделать и обратное определение: если математическое ожидание 
и дисперсия 
случайного процесса не зависят от времени, а корреляционная функция зависит от разности , то процесс считается стационарным в широком смысле. Само определение означает, что оно менее жесткое, и, следовательно, под него подходит большее количество случайных процессов.
|
|
|
Теорема Шеннона для дискретных каналов без шумов и с шумами.
Если в дискретном канале алфавиты кодовых символов 
на входе и 
на выходе одинаковы и
т. е. символы на выходе и входе всегда совпадают, то такой канал называют дискретным каналом без шумов. Он полностью характеризуется основанием кода 
и количеством символов 
, пропускаемых в среднем в единицу времени.
В таком канале количество информации 
содержащееся в принятых символах относительно переданных символов , всегда равно энтропии источника 
. Это следует из того, что: 
так как 
, поскольку при известном значении событие определено однозначно.
Пропускная способность 
дискретного канала без шумов, равная, по определению, максимальному значению 
, достигается в том случае, когда на вход канала поступают символы с максимальной допустимой скоростью от источника, имеющего максимальную энтропию . Для этого необходимо и достаточно, чтобы источник выдавал символы алфавита объемом с равными вероятностями и независимо друг от друга. При этом в соответствии с (1.8) 
и, следовательно,
|
|
|
(2.4)
Теорему кодирования для дискретного канала без шумов в случае источника с управляемой скоростью можно сформулировать следующим образом [1].
Если источник сообщения имеет энтропию H (x) (двоичных единиц на букву), то можно закодировать сообщения источника таким образом, чтобы передавать их сколь угодно точно по дискретному каналу без шумов со средней скоростью 
, букв/сек, (2.5)
где 
— сколь угодно малая положительная величина.
Передавать их сколь угодно точно со скоростью, большей, чем 
, нельзя.
Очевидным следствием этой теоремы, применимым к источнику с фиксированной скоростью, является следующее утверждение.
Сообщения источника с производительностью H’(x) (двоичных единиц в секунду) можно закодировать так, чтобы передавать их сколь угодно точно по дискретному каналу без шумов, при условии, что 
(2.6)
Это невозможно, если
(2.7)
Эти теоремы являются частными случаями теоремы кодирования Шеннона, изложенной в первой главе. Рассмотрим некоторые простейшие случаи их применения.
Терема Шеннона для дискретных каналов связи с шумами.
|
|
|
Если производительность источника сообщений H’ (U) меньше пропускной способности канала С т.е. H’(U)< C то существует такая система кодирования которая обеспечивает возможность передачи сообщений источника со сколь угодно малой вероятностью ошибки (или со сколь угодно малой ненадежностью).
Если H’(U)> C, то можно закодировать сообщение таким образом, что ненадежность в единицу времени будет меньше чем H’(U)-C+ e, где e à0 (прямая теорема).
Не существует способа кодирования обеспечивающего ненадежность в единицу времени меньшую, чем H’(U)-C (обратная теорема).
Дата добавления: 2018-02-18; просмотров: 885; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!