Количественное оценивание плотностей распределения. Начальные и центральные моменты функции.
Если дана случайная величина 
определённая на некотором вероятностном пространстве, то:
§ 
-м нача́льным моментом случайной величины где 
называется величина
если математическое ожидание 
в правой части этого равенства определено;
§ -м центра́льным моментом случайной величины 
называется величина
§ Если определены моменты -го порядка, то определены и все моменты низших порядков 
§ В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:
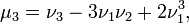
и т. д.
Геометрический смысл некоторых моментов
§ 
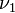равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой.
§ 
равняется дисперсии распределения 
и показывает разброс распределения вокруг среднего значения.
§ 
, будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение
называется коэффициентом асимметрии.
§ 
контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина
называется коэффициентом эксцесса распределения 
Вычисление моментов
§ Моменты могут быть вычислены напрямую через определение путём интегрирования соответствующих степеней случайной величины. В частности, для абсолютно непрерывного распределения с плотностью 
имеем:
|
|
|
если 
а для дискретного распределения с функцией вероятности 
если 
§ Также моменты случайной величины могут быть вычислены через ее характеристическую функцию 
:
§ Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов 
то моменты могут быть вычислены по следующей формуле:
Дискретные экспоненциальные функции: определение и свойства.
Дискретные экспоненциальные функции являются цифровыми аналогами гармонических колебаний. Так как в основе теории сигналов лежит спектральный анализ, основанный на разложении в ряды по системам гармонических функций, то роль этих преобразований трудно переоценить. Гармонические колебания являются базовыми для описания движущихся тел. Как уже принято в технике, в трехмерной системе геометрических координат движения материальной точки по любой из осей 
, 
или 
, (три степени свободы), а также вращения ее по любой из координат (еще дополнительно три степени свободы). Проекция вращения по любой из осей есть гармоническое колебание, т. е. или синус, или косинус. Возможно аналогичное описание на комплексной плоскости проиллюстрированное на рис. 2.3. Как видно из рис. 2.3., вектор имеет две декартовых координаты 
(действительная составляющая) и 
(мнимая составляющая).
|
|
|
Рис. 5.3. Комплексная форма представления колебания
Возможна и вторая форма описания, именуемая в классической математике как система полярных координат, когда состояние вектора оценивается совокупностью двух функций: амплитуды 
и полной фазы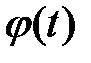 
. Между двумя системами координат существует следующие взаимосвязи:
 ;
 .
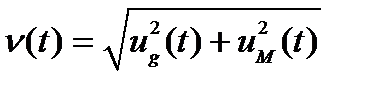| (5.4) |
Существует и пара обратных преобразований:
 ;
 .
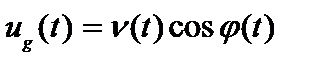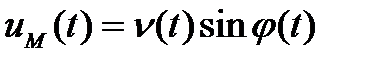| (5.5) |
Выражения (5.4) и (5.5) являются классикой гармонического анализа. Для перехода к ЦОС необходимо представить, что вектор 
по рис.5.4 движется скачками с заданным шагом по фазе 
в положительном направлении. Классическим примером такого движения могут служить электромеханические часы, в которых секундная стрелка совершает 60 скачков за один полный оборот. (Кстати, теперь уже никто не может сказать, почему в минуте 60 секунд, вероятно, это утерянные знания о 60-ричной системе исчисления, существующей у наших далеких предков – гипербореев).
Рис. 5.4. Дискретная экспоненциальная функция
В полярных координатах скачкообразные перемещения вектора 
представляются в виде ДЭФ:
| (5.6) |
|
|
|
Здесь значение 
является минимальным скачком по фазе 
и определяет точность вычислений. Амплитуда вектора нормируется (т. е. равна 1) и «выплывает» только в ходе спектральных преобразований.
Величина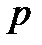 
обычно связывается с номером гармоники, а 
– с аргументом функции.
Предположим, номер функции 
равен 1. Тогда при изменении 
от 0 до 
совершается один полный оборот (см.рис.5.4). Если принять 
, то скачки фазы при изменении аргумента на 1 изменяются на 
. В результате при изменении 
от 0 до 
вектор ДЭФ совершает два полных оборота. В дальнейшем, до 
(или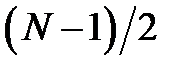 
) при увеличении 
вектор совершает оборотов.
Представим теперь, что 
. Тогда при изменении 
на один шаг вектор изменяет фазу на величину 
, что эквивалентно его «недокручиванию» на величину 
. При следующем шаге по аргументу вектор «недокручивает» на величину 
и т.д. В результате получается, что вектор вращается в отрицательном направлении с основной частотой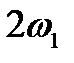 
. Если принять, что 
, то отрицательное вращение вектора соответствует второй гармонике и т. д. таким образом, до значения 
( 
– четное) или 
( – нечетное).
Отметим, что в этом состоит радикальное отличие дискретное представление колебаний от непрерывного. Переход в дискретную область существенно влияет как на конечный результат, так и на способы его интерпретации.
|
|
|
Рассмотрим матричное представление ДЭФ. Обратимся к выражению (5.6) и представим его в виде:
 ,
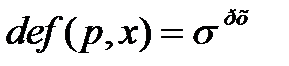| (5.7) |
где 
– дискретный шаг по фазе.
Описание ДЭФ сводится к одному аргументу 
. Принято считать, что 
эквивалентно номеру гармоники. Матрица ДЭФ представляет набор целочисленных аргументов 
, являющихся произведениями 
и 
.
Общие свойства:
1. Свойство нулевого среднего: при любом 
и 
постоянная составляющая функции равна 0:
 .
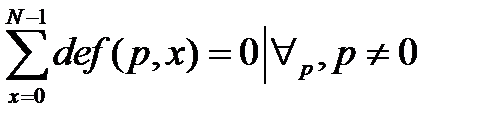| (5.8) |
Это свойство идентично гармоническому ряду, но в непрерывной области. В последнем случае вместо суммы присутствует интеграл. При 
сумма равна 
, что может быть воспринято как нормирующий множитель.
2. Ортогональность. Это очень важное свойство для любой системы разложения в ряд. В данной интерпретации свойство ортогональности принимает вид:
 .
| (5.9) |
Другими словами, разложенные функции при усреднении на интервале из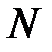 
точек равны 0.
3. Симметричность: замена значений аргумента образует ту же функцию:
 .
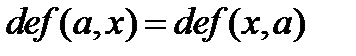| (5.10) |
4. Полнота: при заданном 
система из 
функций 
полная, т. е. любая другая функция представляет одну из имеющихся. Предположим, номер функции равен 
. Тогда эта функция идентична ДЭФ с номером 1.
5. Замкнутость. Является следствием полноты и сводится к следующему:
 ;
 .
| (5.11) |
Выражение (5.11) означает следующее: процедура приводит к функции из замкнутой области 
, причем результирующая функция порядка С образуется как сумма номеров функций по модулю . Так, при 
произведение функций с номерами 7 и 4 даст функцию с номером 2, что легко проверить по матрице (рис.5.13).
Упомянутые процедуры могут продлеваться на любое целочисленное значение . При числовой обработке сигналов практические значения выбираются в других областях: 
256, 512, 1024, 2056 и т. д. (все это степени двойки).
Дата добавления: 2018-02-18; просмотров: 684; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!