Дисперсія випадкових величин. Властивості.
Дисперсією випадкової величини 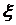 називається математичне сподівання квадрата відхилення цієї величини. Дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання.
називається математичне сподівання квадрата відхилення цієї величини. Дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання.
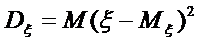 або
або 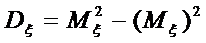
Доведення:
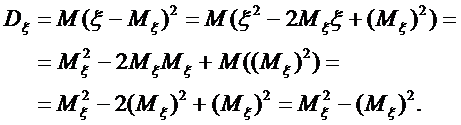
Для дискретної випадкової величини 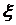 дисперсія:
дисперсія: 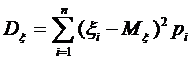
Для неперервної: 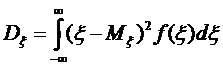
Якщо 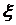 Î [а; b], то
Î [а; b], то 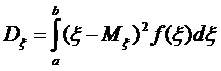
Властивості дисперсії
1. 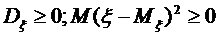
2. Якщо С — стала величина, то
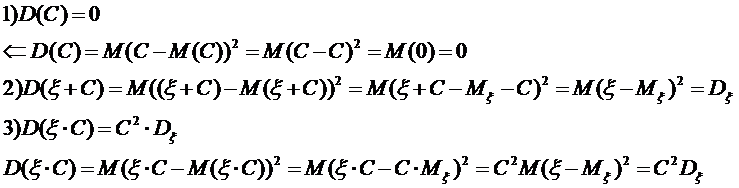 .
.
3. Якщо 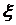 і
і 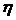 - незалежні випадкові величини, то
- незалежні випадкові величини, то
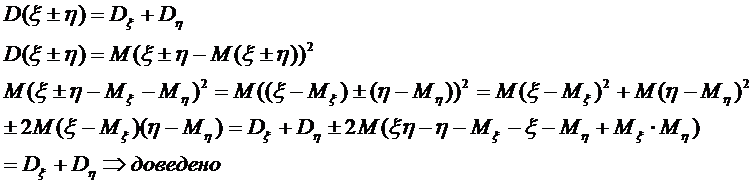
Коефіцієнт кореляції випадкових величин
Коефіцієнт кореляції – міра залежності випадкових величин.
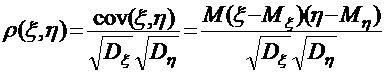 1.
1. 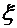 і
і 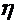 - незалежні, ρ=0. 2. | ρ |≤1.
- незалежні, ρ=0. 2. | ρ |≤1.
Доведення: 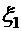 =
= 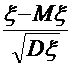 - стандартизована випадкова величина
- стандартизована випадкова величина
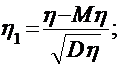
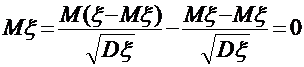 ,
, 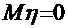 .
.
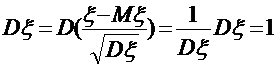 ,
, 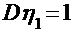 .
.
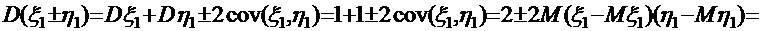
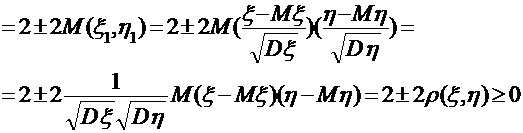
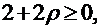
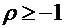 або
або 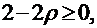
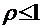 .
.
3. | 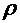 |=1
|=1 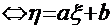
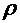 =1, a>0;
=1, a>0; 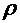 =-1, a<0
=-1, a<0
a) 
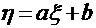
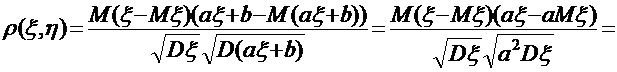
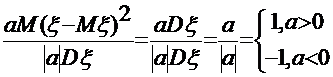
б) 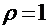
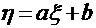
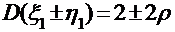 ,
, 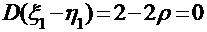
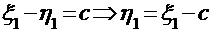 ,
, 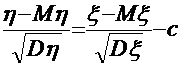
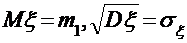 ,
, 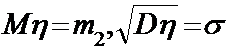
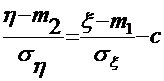
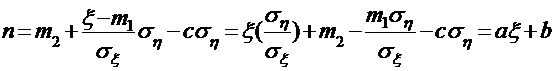
| 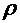 |
| 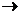 1 – тим сильніша залежність
1 – тим сильніша залежність 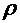 >1 – позитивний звязок (залежність)
>1 – позитивний звязок (залежність) 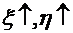
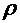 <0 -
<0 - 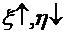
Зауваження: з того, що ρ=0 не впливає незалежність випадкових величин.)
Біноміальний, геометричний та Пуассонівський розподіли. Їх характеристика.
1) Біноміальний розподіл. (Схема Бернулі)
n- нехалежних розподілів
2 результати: - успіх(У) p
-невдача(Н) q
q=1-p p+q=1
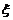 - загальна к-сть усіх успіхів;
- загальна к-сть усіх успіхів; 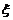 є{0,1,2,…,n}
є{0,1,2,…,n}

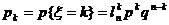
k- У; (n-k) – Н;
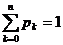 ;
; 
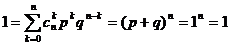 ;
; 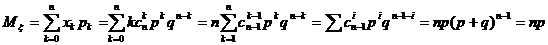
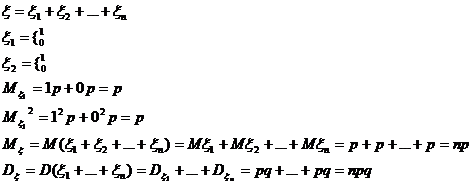
2) Геометричний розподіл.
У – к-сть експериментів, що проводяться до першого успіху
Н – к-сть невдач
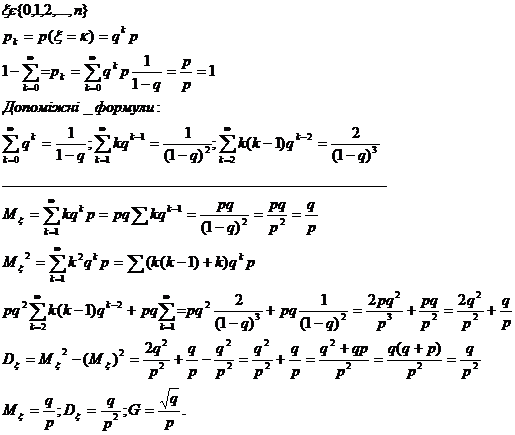
3) Пуассонівський розподіл.
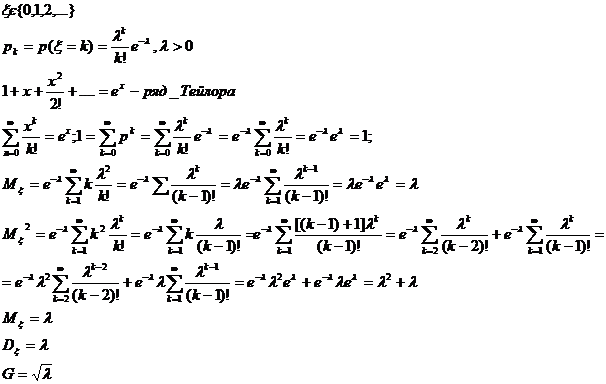
Схема Бернулі. Локальна теорема Муавра-Лапласа
Схема Бернулі(Біноміальний розподіл)
n – кількість незалежних випробувань
|
|
|
У – успіх. p 0≤p≤1
Н – невдача. q=1-p p+q=1
ξ – загальна кількість успіхів в n-експериментах
ξ є{0,1,2…n}
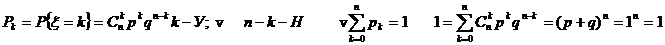
1. математичне сподівання 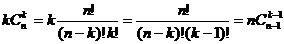
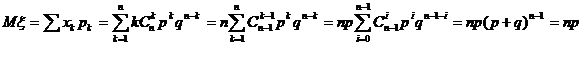
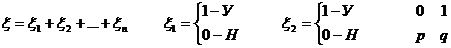
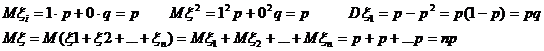
Дисперсія
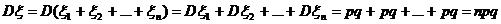
Формули:
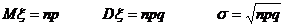
Локальна теорема Муавра-Лапласа
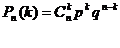
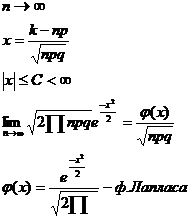
Доведення
Ф-ла Стірлінга: 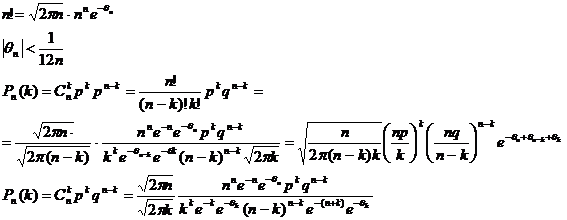
x≤C<+∞
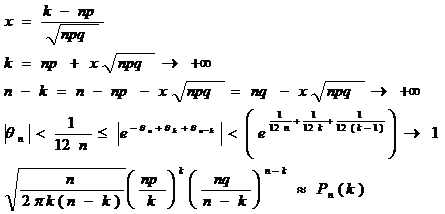
1. 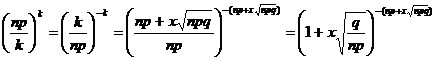
2. 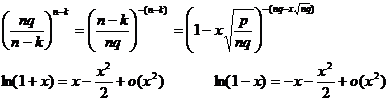
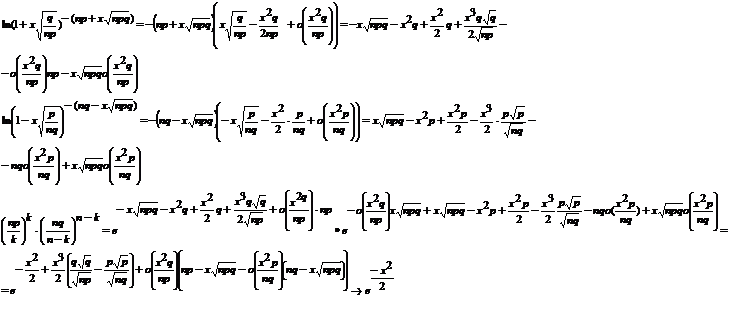
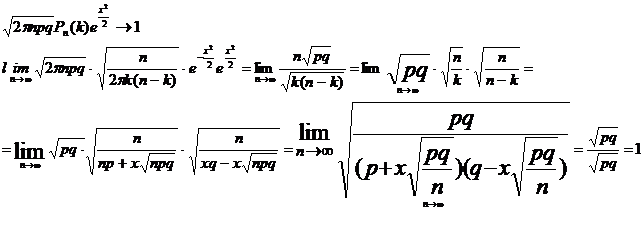
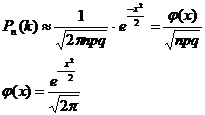
Загальне означення випадкової величини
Нехай 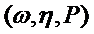 — ймовірнісний простір. Випадковою величиноюназивається функція
— ймовірнісний простір. Випадковою величиноюназивається функція 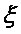 (w) на
(w) на 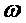 , яка вимірна відносно
, яка вимірна відносно 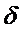 -алгебри
-алгебри 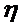 , тобто така функція, коли при кожному дійсному x
, тобто така функція, коли при кожному дійсному x
{w : 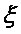 (w) < x}
(w) < x} 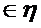 .
.
Функцією розподілу випадкової величини 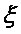 (w)називається функція
(w)називається функція
F(x ) = P{w : 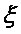 (w) < x}.
(w) < x}.
Функція розподілу F(х) має властивості: а) неперервна зліва; б) неcпадна на 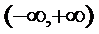 ; в) F(
; в) F( 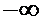 ) =0, F (
) =0, F ( 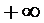 ) = 1.
) = 1.
Для кожної функції F (x), що має ці властивості, можна побудувати ймовірнісний простір
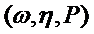 і випадкову величину
і випадкову величину 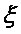 (w) на ньому, яка має функцією розподілу F(х).
(w) на ньому, яка має функцією розподілу F(х).
Якщо F (х) — функція розподілу випадкової величини 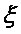 , то
, то
P{a<=x<b}=F(b)–F(a), (a < b).
Функція розподілу, щільність випадкових величин.
Випадковою величиною називається функція x(w)наW, яка вимірна відносно s-алгебри Á, тобто така функція, коли при кожному дійсному x {w : x (w) < x} Î Á, де(W, Á, P)- ймовірнісний простір.
|
|
|
Функцію аргументу х, що визначає ймовірність випадкової події (Х < x), називають функцією розподілу ймовірностей:
F(x ) = P{w : x (w) < x}.
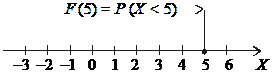 Наприклад, F(5)=P(X < 5) означає, що в результаті експерименту випадкова величина Х (дискретна чи неперервна) може набути значення, яке міститься ліворуч від х = 5, що ілюструє рис.
Наприклад, F(5)=P(X < 5) означає, що в результаті експерименту випадкова величина Х (дискретна чи неперервна) може набути значення, яке міститься ліворуч від х = 5, що ілюструє рис.
Властивості функції розподілу F(x):
1. 0 ≤ F(x) ≤ 1
2. F(x) є неспадною функцією, тобто: F(x2) ≤ F(x1), якщо x2 > x1
3. 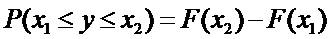 ,(a<b)
,(a<b)
4. F(x) – неперервна зліва
5. F(x) –неспадна a<b; F(a) ≤F(b) P(a≤ 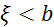 )=F(b)-F(a)>0; F(b)
)=F(b)-F(a)>0; F(b) 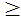 F(a)
F(a)
6. 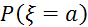
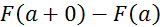 a-т. Неперервності.
a-т. Неперервності. 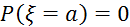
7. 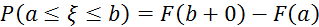
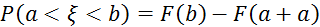
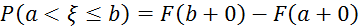
Для кожної функції F (x), що має ці властивості, можна побудувати ймовірнісний простір (W, Á, Р) і випадкову величину x(w) на ньому, яка має функцією розподілу F(х).
Щільність розподілу випадкової величиниx.
Якщо функцію розподілу F(x) випадкової величини x можна подати у вигляді 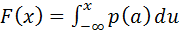
то кажуть, що випадкова величина x має щільність розподілу p(x), і таку випадкову величину називають неперервною.
Майже при всіх x виконується рівність F`(x) = p(x). Щільність розподілу p(x) — невід'ємна функція і 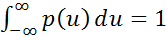
Виконується рівність: 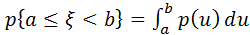
Властивості щільності:
1. 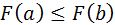 ;
; 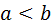
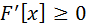
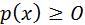
2. 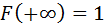
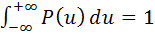
3. 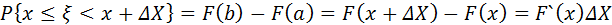 +O(
+O( 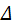 X)
X)
Дата добавления: 2018-02-18; просмотров: 710; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
