Імовірності в дискретних просторах елементарних подій.
Означення Простір Ω елементарних подій називається дискретним,якщо множина Ω скінченна або злічена.
Нехай Ω = {ω1, ω2 , … , ωn, …} дискретний простір елементарних подій. Припустімо, що кожній елементарній події ωk можна поставити у відповідність невід’ємне число pk (ймовірність ωk ), причому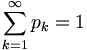 
.
Якщо А - випадкова подія (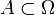 
), то 
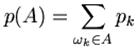, де р(А) - називається ймовірністю події А.
Мають місце властивості:
1. 
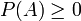(позитивність)
2. 
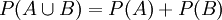, якщо А та В несумісні (адитивність)
3. P(Ω) = 1
Таким чином, ймовірність будь-якої події A лежить у межах: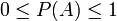 
.
Нехай простір Ω складається з n елементарних рівно можливих подій (pk=1/n, k=1,…,n), а до складу А входять m з цих подій. Тоді P=m/n-класичне означення ймовірності.
Геометричне означення ймовірності.Парадокс Бертрана.Задача Бюффона
Геометрична ймовірність – це поняття ймовірності,що запроваджується так: Нехай Ω - деяка підмножина прямої, площини чи простору. Випадкова подія A - підмножина Ω. Тоді ймовірність випадкової події визначається формулою: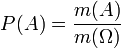 
де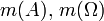 
- довжина, площа чи об’єм множин A та Ω.
Це пов'язане з інтерпретацією ймовірності як міри на обраному просторі елементарних подій. В даному випадку він збігається з eвклідовим простором.
Парадокс Бертрана це задача в класичному означенні ймовірності. Джозеф Бертран вперше описав її вяк приклад того, що ймовірність не може бути чітко означена, поки чітко не описаний механізм отримання випадковостей.
|
|
|
Для деякого кола випадковим чином обирається хорда. Знайти ймовірність того, що ця хорда довша за сторони правильного трикутника, вписаного в це коло. (Варіанти - довша за радіус, або знайтиматсподівання її довжини). Парадокс стверджує що ця ймовірність визначається неоднозначно в залежності від методу.
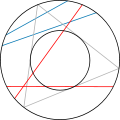
Метод перший.Випадковим шляхом (рівномірно) в даному крузі обирається точка. Ця випадкова точка визначає єдину хорду, серединою якої вона є. Ця хорда довша за сторони нашого вписаного правильного трикутника тоді і тільки тоді, коли її середина лежить всередині кола, вписаного в трикутник. Радіус цього кола дорівнює половині радіуса вихідного кола, отже площа його складає 1/4 площі вихідного. Таким чином, ймовірність того, що випадково обрана точка лежить всередині вписаного кола, дорівнює 1/4. Так що цей метод дає відповідь ¼.
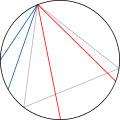
Метод другий.Виходячи з міркувань симетрії, можна вважати, що одним кінцем хорди є фіксована точка на колі. Нехай цією точкою є вершина вписаного трикутника. Оберемо другий кінець випадково з рівномірним розподілом. Вершини трикутника ділять коло на три рівні дуги, і випадкова хорда довша за сторони правильного трикутника, якщо вона перетинає цей трикутник. Так що шукана ймовірність тепер дорівнює ⅓.
|
|
|
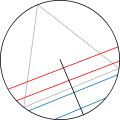
Третій метод.Оберемо точку випадковим чином рівномірно на радіусі кола і візьмемо хорду, яка перпендикулярна цьому радіусу і проходить через обрану точку. Тоді випадкова хорда довша за сторони вписаного правильного трикутника, якщо випадкова точка лежить на тій половині радіусу, який ближчий до центра. Виходячи з міркувань симетрії, неважливо який радіус був обраний для побудови, тому шукана ймовірність дорівнює ½.
Задача Бюффона використовується для статистичного обчислення числа Пі.Площина розграфлена паралельними прямими, які знаходяться на відстані 2a одна від одної. На площину навмання кидають голку завдовжки 2l (2l < 2a). Знайти ймовірність того, що голка перетне одну з прямих.
Зрозуміємо, що означає тут “навмання кинута голка”. Усі можливі положення голки (відрізки) на площині повністю визначаються положенням середини голки і кутом повороту голки відносно якого-небудь напряму. Причому дві ці змінні (положення центру і кут повороту) міняються незалежно один від одного
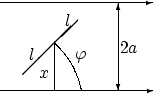
Позначимо через x ∈[0, a] відстань від середини голки до найближчої прямої, а через ϕ ∈[0,π ] — кут між якимсь напрямом прямих і голкою. Множина положень голки цілком визначається вибором навмання точки з прямокутника Ω = [0,π ]×[0,a].Голка пересікає найближчу пряму, якщо координати вибраної навмання точки задовольняють нерівності: x < l ⋅sinϕ .
|
|
|
Площа області A ⊂ Ω , точки якої задовольняють такій нерівності, рівна
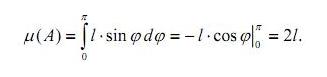
Оскільки μ(Ω) = a ⋅π , то шукана ймовірність дорівнює
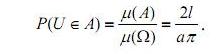
Дата добавления: 2018-02-18; просмотров: 1165; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!