Наслідок теореми неперервності

Теорема Пуасона

- загальна кількість успіхів

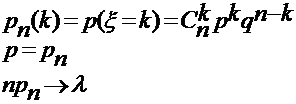
тоді

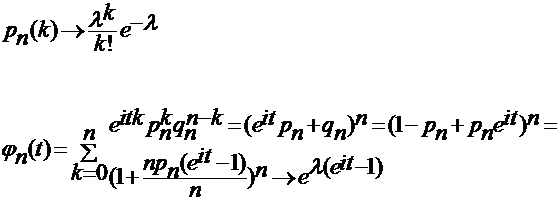
- характеристична функція Пуасона

Теорема Пуассона

Наслідок теореми неперервності

Теорема Пуассона

₁, ₂ … _n -  загальна кількість успіхів

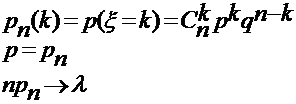
тоді

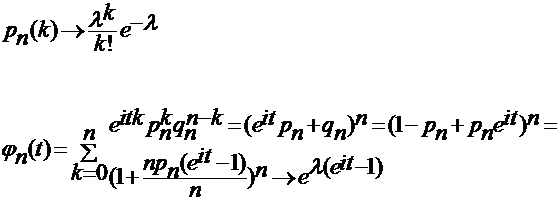
- характеристична функція Пуасона

Наслідок : зберігаються характеристічні функції збігаються розплділи

Закон великих чисел

ξ1, ξ2…ξn- випадкові величини

 будь-яке твердження про збіжність середніх випадкових величин – закон великих чисел.

Теорема Хінчина: нехай ξ1, ξ2…ξn- послідовність незалежних однаково розподілених випадкових величин (пнорвв)

Тоді

Доведемо: якщо ξn

Дов.: Sn=

l(t)= - позначення

=

 

l’(t)=

l’(0)=

  - Характеристичн фунція Sn прямує до а, тоже

Закон великих чисел. Теореми Чебишева та Маркова.

Нехай {ξ_n, n≥1} — (ПНВВ) із скінченними мат сподіваннями a_i=Mξ_i , i≥1. Вважається, що для цієї послідовності виконується закон великих чисел (ЗВЧ), якщо   за ймовірністю, тобто для будь-якого ε > 0  Надалі ξ_n→ ξ, n→∞ за ймовірністю, якщо для будь-якого ε > 0

(збіжність за ймовірністю). Отже будя-яке твердження про збіжність середніх арифметичних випадкових величин носить назву ЗВЧ.

Теорема Чебишева

Якщо { _n, n1} — послідовність незалежних випадкових величин з

M_k a_k , DC , k 1, то для неї виконується ЗВЧ

Доведення:

  

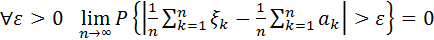
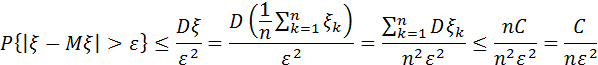
Теорема Маркова

Якщо { _n, n1} — послідовність незалежних випадкових величин зM_k a_k ,

   то для неї виконується закон великих чисел.

Наслідок:

Якщо { _n, n1} — ПНВВ зM_k a_k , n≥1 тоді   і для неї виконується ЗВЧ.

Нехай { _n, n1}— послідовність таких незалежних випадкових величин, що

Тоді вважається, що для послідовності { _n, n1}виконується:

а) умова Ліндберга, якщо для

б) умова Ляпунова, якщо для деякого δ 0

Центральна гранична теорема

(послідовні незалежні однаково розподілені випадкові величини)

M =a

p<D =

тоді:

dt

 

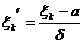- стандартизовані випадкові величини

 

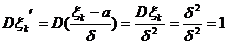
Наслідок – Інтегральна теорема М.-Л.

           1    g p

{0 h q

 

a=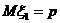

 

Умова Лінденберга, Теорема Ляпунова

Умова Лінденберга

 

Т.Ляпунова

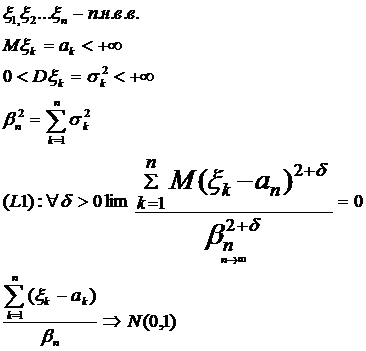
Твердження

!!! L і L1 будуть виконуватись для ЦГТ, якщо п. рівномірно мала.

Дискретні ланцюги Маркова. Матриця перехідних ймовірностей.

 – дискретні випадкові величин.

Послідовність

       – додатні цілі значення

Називається Ланцюгом Маркова

Якщо для  цілих додатних

               

Виконується рівність

 

 

 – ймовірність пероходу iз стану  в стан  на -тому кроці;

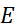 – множина станів ланцюга Маркова

Якщо  однакова, тоді ланцюг називається однорідним

 – матриця переходу ймовірностей за 1 крок

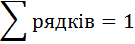
Будь-яка матриця називається стохастичною

 – матриця переходу за  кроків

 – стохастична матриця переходу за  кроків

 

Рівність Чепмена-Колмогорова

 

 

Класифікація станів дискретного ланцюга Маркова

К1: Стан ієЕ назив. неістотним, якщо стан j та n є Z,P_ij(n)>0, але p_ij(m)=0 (назад не вертається), в протилежному випадку стан істотний.

Е=Е₀(істот) Е₁(неістот)

К2: два істотних стани i,j є Е₀, називаються істотні стани, що сполучаються i j, якщо  n, s P_ij(n)>0, P_ij(s)>0.

 - відношення на множині цілих чисел; відношення буде задовільним, якщо викон-ся 3 властивості:

1) рефлективність: i j

2) симетричність: i j  j i

3) транзитивність: якщо i k, a k j, то j i

Якщо відношення задовольняють умови 1,2,3 то таке відношення називається відношенням еквівалентності.

Теорема

Відношення еквівалентності розбиває Е на перетинаючи класи еквівалентності Е₀= 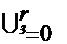Е_0і, r>=1.

E=E₀₁ – неістотний ланцюг,якщо r=1, E₁= .

Приклади

P= ( )  

Е₁={1,3}, E₀={2,4}  

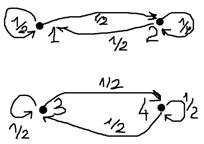             E₀={1,2,3,4}; E₀₁={1,2}; E₀₂={3,4}

K3: істотний стан ієЕ₀ має період d, d=НСД(={n;p_ii>0}

Якщо i(стрілка сам в себе),то d=1, стан неперіодичний

К4: істотний стан і називається рекурентним, якщо , і нерекурентним, якщо . f_i(n) – ймовірність І раз повернутися в стан і на n-ому кроці. f_i(n)=P{ =i, }

Якщо множина станів Е скінчена, то будь-який істотний стан – рекурентний.

Рекурентні ланцюги Маркова.

Істотний стан іоднорідного ланцюга Маркова називається рекурентним, якщо  і не рекурентним, якщо , де   - ймовірність перший раз повернутися в і на 1-му кроці.

Якщо множина станів Е – скінчена, то істотний стан – рекурентний.

Теор.Істотний стан рекурентний тоді, коли

Довед.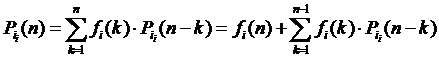

 

---

Дата добавления: 2018-02-18; просмотров: 1153; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!