Аналіз нелінійних систем методом гармонічного балансу
Метод гармонічного балансу полягає в тому, що виділяють основна гармоніка сигналу і розглядають проходження її через систему.
Нелінійна частина системи змінює сигнал, який поступає на неї. Якщо на нелінійний елемент подавати гармонічний сигнал, то на його виході буде сигнал складної форми, як це показано на рис.8.2. Цей сигнал містить ряд гармонічних складових. Сигнал, перетворений нелінійним елементом, проходить через лінійну частину системи. Лінійна частина, як ми вже знаємо, має амплітудно-частотну характеристику, що пропускає, як правило, низькі частоти і значно ослабляє високі частоти. Для аналізу динаміки систем методом гармонічного балансу вихідний сигнал нелінійної частини розкладають у ряд Фур’є і виділяють у ньому основну гармоніку. Аналізують роботу лінійної системи і вивчають динаміку при виділеному гармонічному сигналі. Тобто лінійну систему розглядають як фільтр, який пропускає тільки сигнали певних частот. Ситуація виглядає так, що нелінійний елемент тільки змінює фазу й частоту синусоїдальних коливань. Лінійна частина виконує перетворенні того сигналу.
Для аналізу умов виникнення автоколивань згідно з методом гармонічного балансу лінійну частину системи описуємо його передатною функцію та амплітудно-фазовою частотною характеристикою W(ω). Нелінійний елемент також описуємо його амплітудно-фазовою частотною характеристикою Z(ω). Ця характеристика може бути розрахована або знайдена експериментально. Проте для типових нелінійних елементів немає потреби вивчати і розраховувати АФЧХ, оскільки вони наведені в довідниках. Для визначення умов виникнення автоколивань будують на одному з графів АФЧХ розімкнутої лінійної частини системи W(ω) та АФЧХ нелінійного елемента. Z(ω ). За аналізом їх розміщення визначають можливість виникнення автоколивань та їх параметри. Приклад побудови АФЧХ показано на рис.8.4. Точка перетину АФЧХ лінійної частини W(ω) та нелінійної частини Z(ω) визначає можливість виникнення коливань і їх параметри. Частота коливань відповідає розміщенню точок за частотою при побудові АФЧХ, а амплітуда відповідає модулю АФЧХ в точці перетину. Причому стійким коливанням відповідає тільки одна точка перетину. Щоб позбутися автоколивань, коли вони небажані, потрібно змінити параметри лінійної системи так, щоб АФЧХ її не перетиналась з АФЧХ нелінійного елемента. Це можна зробити, як показано на рис. 8.4, зміною коефіцієнта підсилення лінійної частини або іншим шляхом.

Рис. 8.4 – Визначення автоколивань нелінійної системи
Аналіз нелінійних систем за фазовими траєкторіями
Іншим методом аналізу динаміки нелінійних систем є методи побудова фазової площини чи фазового простору і вивчення фазового портрету нелінійної системи.
Фазовою площиною називають площину, осями якої є значення вихідної величини x та швидкість її зміни y = x’.
Фазовою траєкторією є графік зміни вихідної величини x та швидкість її зміни y = x’ протягом перехідного процесу.
Фазовим портретом є сукупність фазових траєкторій, одержаних при різних початкових умовах
Побудова фазової траєкторій на прикладі перехідного процесу показана на рис.8.5. Для кожної точки перехідного процесу встановлюють значення вихідної величини системи і швидкість її зміни. Ця фазова траєкторія відповідає затуханню коливань і точка в початку координатної осі є точкою стійкості системи.
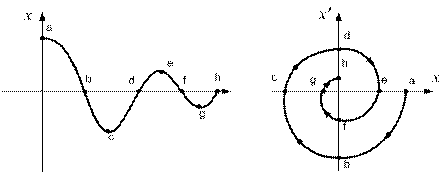
Рис.8.5 – Побудова фазової траєкторії за перехідним процесом
Для аналізу динаміки нелінійних САК фазові траєкторії будують згідно з рівнянням динаміки системи. Фазова площина відповідає системі, порядок якої рівний двом, тобто системі, в якої в рівняння динаміки входять тільки похідні другого порядку. Рівняння такої системи можна подати у вигляді
 (8.1)
(8.1)
Тут F(х) –нелінійна функція від х. Позначимо y = х’.
Тоді рівняння можна записати так
 (8.2)
(8.2)
Звідси
 (8.3)
(8.3)
Виключивши з рівняння параметр t, одержимо
 (8.4)
(8.4)
Це є рівняння фазових траєкторій.
Побудувати фазові траєкторії можна числовим методом. Для кожних значень початкових умов фазові траєкторії будуть різні, а їх сукупність буде фазовим портретом нелінійної системи.
У випадку рівняння третього порядку вводять три змінні. Позначають y = х’. z = y = x” Тут ми маємо тривимірний фазовий простір. Побудова фазових траєкторій в тривимірному просторі звичайно більш важка, але ніяких принципових обмежено не має. Поняття фазових простір можна узагальнити на більш складні системи і розглядати багатовимірні фазові простори. Математики в цьому ніяких особливих проблем не бачать. Аналіз виконують, як правило, використовуючи двовимірні січення простору.
За фазовим портретом системи аналізують її поведінку в різних режимах роботи. Вигляд фазового портрету дає наглядне уявлення про динаміку нелінійних систем керування. Розглянемо деякі прилади фазових портретів систем та особливості динаміки таких систем.
На рис. 8.6 показано найпростіші фазові портрети систем. Вони характеризують стійку й нестійку системи. У випадку рис.8.6, а коливання в системі затухають, а у випадку рис.8.6, б – наростають.

Рис. 8.6 – Фазові портрети: а) - стійкої та б) – нестійкої систем
Більш складні фазові портрети можуть мати вигляд показаний на рис. 8.7. Рис. 8.7, а відповідає стійкій системі в „малому” і нестійкій в „великому”. Коли зображуюча точка знаходиться всередині еліпса (амплітуда коливань не перевищує критичної величини), система є стійкою і коливання в ній затухають. Якщо зображуюча точка знаходиться поза еліпсом, то коливання наростають і система є нестійкою.

Рис. 8.7 – Фазові портрети систем , яким властиві автоколивання
Рис. 8.7, б) відповідає системі, в якої є стійкі автоколивання. Якою б не була початкова точка на фазовій траєкторії, завжди динаміка системи направлена на те, що в кінцевому результаті будуть здійснюватись автоколивання, що відповідають замкнутій фазовій траєкторії.
Ряд систем другого і більш високих порядків мають значно складніші фазові портрети. Такі системи можуть мати декілька різних циклів автоколивань. Приклад фазового портрету системи. якій властиві два типи автоколивань, показано на рис. 8.8. Як видно з наведених рисунків процеси в нелінійній системах можуть бути досить складними і їх вивчення є не тільки важким, але й цікавим завданням.
Підводячи підсумки зауважимо, що нелінійні системи , як правило, не можна характеризувати як стійкі чи нестійкі системи. Система може бути стійкою при одних значеннях параметрів і нестійкою при інших. При цьому в системі можуть виникати автоколивання. При деяких початкових значеннях діючих величин ці автоколивання можуть виникати , а при інших ні. Динаміка нелінійних систем досить складна і кінцеві значення величини керування можуть залежати не тільки від параметрів системи а і від початкових умов.
Дата добавления: 2018-02-15; просмотров: 574; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
