Частотні критерії якості перехідних процесів
Частотні критерії оцінки якості перехідних САК базуються на залежності перехідних процесів від частотних характеристик системи. Вони найбільш зручні під час використання частотних методів розрахунку та експериментального дослідження властивостей САК. Особливо вони незамінні, коли характеристики деяких елементів, що входять до складу САК, подаються у вигляді частотних характеристик. Основою частотних методів є логарифмічні амплітудно- та фазово-частотні характеристики, амплітудно-фазова, дійсна та уявна частотні характеристики. Частотні методи оцінки якості САК досить різноманітні, тут ми розглянемо тільки деякі з них.
Визначення якості перехідних процесів за АФЧХ розімкнутої системи.
За виглядом АФЧХ можна визначити величину запасу стійкості системи і якість перехідних процесів. . Запас стійкості системи згідно АФЧХ визначають за модулем та фазою. Якість роботи системи в перехідних режимах також залежить від величини запасу стійкості. Чим більший запас стійкості, тим швидше затухають перехідні процеси, тим якіснішою є система. У загальному вигляді, коли початкова частина АФЧХ має вигляд, показаний на рис. 7.16, якість перехідних процесів можна знайти за величиною, яка характеризує запас стійкості системи.
Рис. 7.16 – Загальний вигляд початкової частини АФЧХ розімкнутої системи
Як показник якості перехідного процесу та запасу стійкості за модулем АФЧХ визначають розміщенням точки перетину АФЧХ з дійсною віссю комплексної площини. Величину запасу стійкості за модулем можна знайти згідно з формулами:
|
|
|
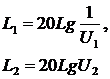(7.42)
відповідно до розміщення точки перетину дійсної осі, як це показано на рис.7.16.
Величину запасу стійкості за фазою визначають як величину кута, на який потрібно повернути АФЧХ, щоб вона перетнула дійсну вісь в точці (-1, j0). Цей кут дорівнює:
. (7.43)
Кут ψ – це значення фази в точці, в якій модуль АФЧХ дорівнює 1. (Знак + тут стоїть з огляду на те, що фазовий зсув має від’ємне значення).
Для придатних до експлуатації САК, в яких перехідний процес швидко загасає, прийнято відносити системи, в яких величина L1 і L2 дорівнює приблизно 6 – 20 дБ, що в лінійному масштабі відповідає 2 – 10. Запас стійкості за фазою для придатних до експлуатації САК прийнято вважати 300 – 600.
Визначення якості перехідних процесів за дійсною та уявною частотними характеристиками
Якість перехідних процесів САК можна також оцінити за дійсною та уявною характеристиками САК. Ці характеристики дають повну інформацію про перехідні процеси системи, оскільки вони взаємозв’язані між собою. Проте в більшості випадків використовують дійсну частотну характеристику. Визначити дійсну частотну функцію можна з комплексної передаточної функції (КПФ). Запис КПФ в алгебраїчній формі визначає дійсну і уявну частотні функції:
|
|
|
. (7.44)
За дійсною частотною функцією P(ω) можна побудувати перехідну характеристику системи. Для цього використовують спеціальні h – функції, параметри яких подані в ряді літературних джерел, наприклад в [1]. Графік дійсної частотної функції, побудований для суттєвих частот, показано на рис. 7.17.
Рис.7.17 – Вигляд дійсної частотної функції САК
Суттєвими частотами вважають частоти, для яких значення дійсної частотної функції не менше 0,1 максимальної величини. Тобто область суттєвих частот визначають згідно з умовою:
. (7.45)
Не вдаючись в особливості побудови перехідних характеристик наведемо основні висновки про залежність якості перехідних процесів від вигляду дійсної частотної характеристики системи:
1. Наявність розриву дійсної частотної характеристик на певній частоті свідчить, що один з коренів характеристичного полінома є чисто уявним і система знаходиться на межі стійкості.
|
|
|
2. Наявність гострого і високого піка P(ω) свідчить про значну коливальність системи і повільне згасання перехідного процесу.
3. Щоб перерегулювання не перевищувало 18%, P(ω) повинна бути не зростаюча, тобто при P(ω)>0 
< 0.
4. Максимальне значення перерегулювання можна розрахувати за формулою:
.
5. Умова монотонності перехідного процесу така:
.
6. Якщо P(ω) приблизно описується трапецією, то тривалість перехідного процесу знаходиться в межах
.
Дата добавления: 2018-02-15; просмотров: 1128; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!