Применение статических методов в теории надежности (определение, расчетные формулы).

⇐ ПредыдущаяСтр 65 из 76Следующая ⇒

Статисти́ческиеме́тоды — методы анализа статистических данных. СТАТИСТИЧЕСКИЕ МЕТОДЫ — научные методы описания и изучения массовых явлений, допускающих количественное (численное) выражение.

Целесообразно выделить три вида научной и прикладной деятельности в области статистических методов анализа данных (по степени специфичности методов, сопряженной с погруженностью в конкретные проблемы):

а) разработка и исследование методов общего назначения, без учёта специфики области применения;

б) разработка и исследование статистических моделей реальных явлений и процессов в соответствии с потребностями той или иной области деятельности;

в) применение статистических методов и моделей для статистического анализа конкретных данных.

Количественные показатели надёжности(Н). Н. изделий определяется набором показателей; для каждого из типов изделий существуют рекомендации по выбору показателей Н. Для оценки Н. изделий, которые могут находиться в двух возможных состояниях — работоспособном и отказовом, применяются следующие показатели: среднее время работы до возникновения отказа Т_ср — Наработка до первого отказа; среднее время работы, приходящееся на один отказ, Т — Наработка на отказ;Интенсивность отказов λ(t); Параметр потока отказов ω(t); среднее время восстановления работоспособного состояния τ_в;Вероятность безотказной работы за время t [Р (t)]; Готовности коэффициент K_r.

Закон распределения наработки до отказа определяет количественные показатели Н. невосстанавливаемых изделий. Закон распределения записывается либо в дифференциальной форме плотности вероятности f(t), либо в интегральной форме F(t). Существуют следующие соотношения между показателями Н. и законом распределения:

Для восстанавливаемых изделий вероятность появления n отказов за время t в случае простейшего потока отказов определяется законом Пуассона:

Из него следует, что вероятность отсутствия отказов за время t равна Р (t) = exp(-λt) (экспоненциальный закон надёжности).

Технические системы, состоящие из конструктивно независимых узлов, обладающие способностью перестраивать свою структуру для сохранения работоспособности при отказе отдельных частей, в теории Н. принято называть сложными техническими системами (в отличие от сложных кибернетических систем, называются также большими системами. Число работоспособных состоянии таких систем — два и более. Каждое из работоспособных состояний характеризуется своей эффективностью работы, которая может измеряться производительностью, вероятностью выполнения поставленной задачи и т.д. Показателем Н. сложной системы может быть суммарная вероятность работоспособности системы — сумма вероятностей всех работоспособных состояний системы.

Способы определения количественных показателей надёжности. Показатели Н. определяются из расчётов, проведением испытаний и обработкой результатов (статистических данных) эксплуатации изделий, моделированием на ЭВМ, а также в результате анализа физико-химических процессов, обусловливающих Н. изделия. Расчёты Н. основаны на том, что при определенной структуре изделия и имеющемся законе распределения наработки до отказа изделий этого типа существуют вполне определенные зависимости между показателями Н. отдельных элементов и Н. изделия в целом. Для установления таких зависимостей используются следующие приемы: решение уравнении, составленных на основании структурной схемы Н. (использование последовательно-параллельных структур) или на основании логических связей между состояниями изделия (использование алгебры логики); решение дифференциальных уравнений, описывающих процесс перехода изделия из одного состояния в другие (использование графов состояний); составление функций, описывающих состояния сложного изделия. Расчёты Н. производятся главным образом на этапе проектирования изделий с целью прогнозирования для данного варианта изделия ожидаемой Н. Это позволяет выбрать наиболее подходящий вариант конструкции и методы обеспечения Н., выявить «слабые места», обоснованно назначить рабочие режимы, форму и порядок обслуживания изделия.

Испытания на Н. производятся на этапах разработки опытного образца и серийного производства изделия. Существуют испытания на Н. определительные, в результате которых определяют показатели Н.; контрольные, имеющие целью контроль качества технологического процесса, обеспечивающего с некоторым риском Н. не ниже заданной; ускоренные, в ходе которых используют факторы, ускоряющие процесс возникновения отказов; неразрушающие, основанные на применении методов дефектоскопии и интроскопии, а также на изучении косвенных признаков (шумов, тепловых излучений и т.п.), сопутствующих возникновению отказов.

Моделирование на ЭВМ является наиболее эффективным средством анализа Н. сложных систем. Широко распространены два алгоритма моделирования: первый, основанный на моделировании физических процессов, происходящих в исследуемом объекте (оценка Н. при этом определяется по числу выходов параметров объекта за пределы допуска); второй, основанный на решении систем уравнений, описывающих состояния исследуемого объекта.

Анализ физико-химических процессов также позволяет получить оценку Н. исследуемого изделия, т.к. часто удаётся установить зависимость Н. от состояния и характера протекания физико-химических процессов (соотношение показателей прочности и нагрузки, износостойкость, наличие примесей в материалах, изменение электрических и магнитных характеристик, шумовые эффекты и т.д.). Наиболее часто анализ физико-химических процессов применяется при оценке Н. элементов радиоэлектронной аппаратуры.

Методы:

Статистический приемочный метод- совокупность методов статистич. контроля качества массовой промышленной продукции с целью выявления еe соответствия заданным требованиям. С. п. к. ведется на основе государственных стандартов (ГОСТ), содержащих таблицы планов контроля и правила выбора планов из этих таблиц. Предусматривается возможность ведения контроля на разных уровнях жесткости При выборе плана контроля и уровня жесткости учитывают объем контролируемой партии (число входящих в нее изделий), результаты контроля предыдущих партий и др. факторы. С. п. к - действенное средство поддержания требуемого уровня качества продукции.
Наиболее часто используются две разновидности С. п. к. - контроль по альтернативному признаку и контроль по количественному признаку. При контроле по альтернативному признаку изделия классифицируются на годные и дефектные. При контроле по количественному признаку измеряются параметры изделий, принимающие вещественные значения.
При отборе изделий на контроль используются различные методы. Широко используется случайный выбор без возвращения при к-ром все выборки одинакового объема имеют равные вероятности. Eсли контроль носит разрушающий характер (испытания на разрыв), то сплошной контроль невозможен. При С. л. к., как правило, проверяется лишь часть изделий, составляющих выборку, поэтому возможны ошибочные решения. В теории С. п. к. разрабатываются методы расчета вероятностных показателей планов контроля и статистич. методы оценки эффективности С. п. к. на основе накапливаемой информации о ходе контроля Часто С. п. к. проводят с использованием одноступенчатых планов. Пусть - контролируемая партии из Nизделий. Одноступенчатый план характеризуется заданием объема пвыборки и приемочным числом с. 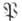Если число дефектных изделий в выборке окажется равным dи то принимается. Если же d>c, то бракуется. В зависимости от вида изделий решение о браковке может либо означать сплошную проверку всех изделий из не попавших в выборку, либо снижение сортности и т. п. В стандартах допускается использование двухступенчатых, многоступенчатых и последовательных планов. Двухступенчатый план характеризуется заданием объемов n и n₂ первой и второй выборок, приемочных чисел c₁,c₂, браковочных чисел r₁, r₂(r₁>c₁, r₂=c₂+l). Если число дефектных изделий в первой выборке то принимается. Если 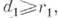то бракуется. В том случае, когда с ₁<d₁<r₁, берется вторая выборка. 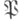Если d₂- число дефектных изделии во второй выборке и то принимается. Если 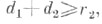то бракуется.
Важной числовой характеристикой планов С. п. к. при контроле по альтернативному признаку является оперативная характеристика Р(D), равная вероятности принять партию по результатам контроля изделий, составляющих выборку. Для одноступенчатого плана

где

вероятность обнаружить dдефектных изделий в случайной выборке без возвращения объема n, когда содержит Dдефектных изделий. Распределение с вероятностями d=0,. . ., п, наз. гипергеометрическим. Расчет числовых показателей планов контроля часто проводится на основе аппроксимации гипергеометрического распределения биномиальным или пуассоновским распределениями. Для двухступенчатых и последовательных планов существенным показателем является среднее число контролируемых изделий m(D).

Статистическое регулирование технологических процессовЗадача статистического регулирования технологического процесса состоит в том, чтобы на основании результатов периодического контроля выборок малого объема приходить к заключению: "процесс налажен" или "процес разлажен". Выявление разладки технологического процесса основано на результатах периодического контроля малых выборок, осуществляемого по количественному или альтернативному признакам. Для каждого из этих способов контроля используются свои статистические методы регулирования.Контроль по количественному признаку заключается в определении с требуемой точностью фактических значений контролируемого параметра у единиц продукции из выборки. Фактические значения контролируемого параметра необходимы для последующего вычисления статистических характеристик, по которым принимается решение о состоянии технологического процесса. Такими характеристиками являются медиана и выборочное среднее; квадратическое отклонение и размах.

Первые две характеристики - характеристики положения, а последние две - характеристики рассеивания случайной величиныХ.

Контроль по альтернативному признаку заключается в определении соответствия контролируемого параметра или единицы продукции установленным требованиям. При этом каждое отдельное несоответствие установленным требованиям считается дефектом, а единица продукции, имеющая хотя бы один дефект, считается дефектной.

При контроле по альтернативному признаку не требуется знать фактическое значение контролируемого параметра - достаточно установить факт соответствия или несоответствия его установленным требованиям. Поэтому можно использовать простейшие средства контроля: шаблоны, калибры, контроль по образцу и др. Решение о состоянии технологического процесса принимается в зависимости от числа дефектов или числа дефектных единиц продукции, обнаруженных в выборке. Каждый из перечисленных способов контроля имеет свои преимущества и свои недостатки. Преимущество контроля по количественному признаку состоит в том, что он более информативен (по сравнению с контролем по альтернативоному признаку) и поэтому требует меньшего объема выборки. Однако такой контроль более дорогой, поскольку для него необходимы такие технические средства контроля, которые позволяют получать фактические значения контролируемого параметра. Кроме того, для статистического регулирования при контроле по количественному признаку необходимы вычисления, связанные с определением статистических характеристик.

Преимущество контроля по альтернативному признаку заключается в его простоте и относительной дешевизне, поскольку можно использовать простейшие средства конртоля или визуальный контроль. К недостаткам такого контроля относится его меньшая информативность, что требует значительно большего объема выборки при равных исходных данных.

С учетом изложенных фактов выбирают тот или иной способ контроля для статистического регулирования. Рассмотрим суть статистических методов регулирования технологических процессов.

Любой контролируемый параметр по своей природе является случайной величиной, поскольку он может принять то или иное значение, причем заранее нам неизвестное.

Случайная величина (показатель качества - масса, диаметр отверстия, вала и пр.) может быть, в частности, непрерывной или дискретной. Например, диаметр вала представляет собой непрерывную случайную величину, которая теоретически может принимать все значения в интервале, ограниченном допуском, скажем, между 34,5 и 35,5 мм. Непрерывную величину мы получаем при контроле качества продукции по количественному признаку с помощью измерительных средств, позволяющих получить значение контролируемого параметра с большой точностью.

Дискретную величину мы получаем, например, при контроле качества продукции по альтернативному признаку "годен" или "не годен". В результате такого контроля мы подсчитываем число дефектных единиц или число дефектов. При этом нас не интересует истинное значение параметра Х, достаточно лишь установить соответствует ли оно установленному требованию или нет.Наиболее часто применяемым при решении задач статистического контроля качества распределением непрерывной случайной величины Х является нормальное распределение.

Дата добавления: 2018-02-15; просмотров: 1354; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 60 61 62 63 646566 67 68 69 Следующая ⇒

Мы поможем в написании ваших работ!