Преобразование звезды в треугольник.

⇐ ПредыдущаяСтр 64 из 76Следующая ⇒

Существо способа преобразования с помощью эквивалентной замены треугольника на звезду и обратно заключается в том, что узел сложной конфигурации заменяется на узел другой, более простой конфигурации, но при этом подбираются такие характеристики нового узла, что надежности преобразуемой цепи сохранялись прежними.

Пусть, например, требуется заменить треугольник (рис. 4.5.7,а) звездой (рис. 4.5.7,б) при условии, что вероятность отказа элемента a равна q₁₃, элемента b равна q₁₂, элемента c - q₂₃. Переход к соединению звездой не должен изменить надежность цепей 1-2, 1-3, 2-3. Поэтому значение вероятностей отказов элементов звезды q₁, q₂, q₃ должны удовлетворять следующим равенствам:
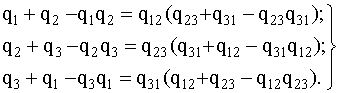(4.5.14)

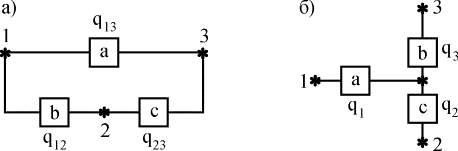
Рис. 4.5.7. Преобразование "треугольник - звезда"

Если пренебречь произведениями вида q_iq_j; q_iq_jq_k, то в результате решения системы уравнения (4.5.14) можно записать:
q₁=q₁₂q₃₁; q₂=q₂₃q₁₂; q₃=q₃₁q₂₃. (4.5.15)

Для обратного преобразования звезды в треугольник
q₁₂= 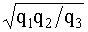; q₂₃= ; q₃₁= 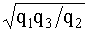. (4.5.16)

Пример 4.5.7. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9, а вероятности отказов равны 0,1.

Решение.
1. Преобразуем соединение элементов 1,2,5 в треугольник (рис. 4.5.8,а), в звезду (рис. 4.5.8, б).

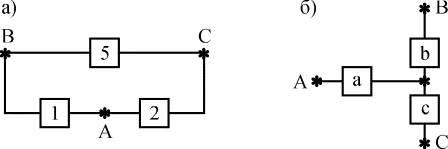
Рис. 4.5.8. К примеру преобразования структуры

Пример разложения мостиковой структуры по базовому элементу.

Способ преобразования с помощью разложения сложной структуры по некоторому базовому элементу основан на использовании теоремы о сумме вероятностей несовместных событий. В сложной структуре выбирают базовый элемент (или группу базовых элементов) и делаются следующие допущения:
- базовый элемент находится в работоспособном состоянии;
- базовый элемент находится в отказавшем состоянии.

Для этих случаев, представляющих собой два несовместных события, исходная структура преобразовывается в две новые схемы. В первой из них вместо базового элемента ставится "короткое замыкание" цепи, а во второй - разрыв. Вероятности безотказной работы каждой из полученных простых структур вычисляются и умножаются: первая - на вероятность безотказного состояния базового элемента, вторая - на вероятность отказа базового элемента. Полученные произведения складываются. Сумма равна искомой вероятности безотказной работы сложной структуры.

Пример 4.5.8. Решить предыдущий пример методом разложения сложной структуры.

Решение.

1. В качестве базового элемента примем элемент 5 (рис. 4.5.3,б).

2. Закоротим базовый элемент, т.е. сделаем допущение об абсолютной его проводимости. Присоединим к полученной структуре последовательно базовый элемент с характеристикой его надежности р₅. В результате вместо исходной структуры получим новую структуру (рис. 4.5.10,а).

Рис. 4.5.10. Пример разложения мостиковой структуры по базовому элементу

3. Произведем обрыв базового элемента, т.е. сделаем предположение об его абсолютной ненадежности (непроводимости). К полученной структуре присоединим последовательно базовый элемент с характеристикой его ненадежности (1-р₅). В результате получим структуру (рис. 4.5.10,б).

4. Искомая вероятность равна сумме вероятностей структур (рис. 4.5.10,а,б), каждая из которых параллельно-последовательная. Поэтому

Р = р₅[(р₁+р₂-р₁р₂)(р₃+р₄-р₃р₄)] + (1-р₅)[р₁р₃+р₂р₄-р₁р₃р₂р₄]=
= 0,9[(0,9+0,9 - 0,90,9)  (0,9+0,9 - 0,90,9)] +
+ (1-0,9)  [0,90,9 + 0,90,9 - 0,90,90,90,9]0,978.

Вероятность безотказной работы мостиковой схемы, состоящей из пяти неодинаковых и независимых элементов, можно определить по формуле:

Р=2р₁р₂р₃р₄р₅-р₂р₃р₄р₅-р₁р₃р₄р₅-р₁р₂р₄р₅-р₁р₂р₃р₅-
-р₁р₂р₃р₄+р₁р₃р₅+р₂р₃р₄+р₁р₄+р₂р₅. (4.5.17)

В случае идентичных элементов эта формула принимает вид

Р = 2р⁵-5р⁴+2р³+2р². (4.5.18)

Подставляя соотношение (4.5.18) в формулу (4.5.4), получаем, что в случае использования элементов с постоянной интенсивностью отказов (экспоненциальном законе распределения отказов)

Р(t) = 2ехр(-5t)-5ехр(-4t)+2ехр(-3t)+2ехр(-2t). (4.5.19)

Среднее время безотказной работы системы Т₀ находим, путем интегрирования уравнения (5.19) в интервале [0,]:

Т₀ = 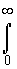2ехр(-5lt)-5ехр(-4lt)+2ехр(-3lt)+2ехр(-2lt)dt=
= (49/60)´(1/l). (4.5.20)

Резервирование – метод повышения характеристик надёжности технических устройств или поддержания их на требуемом уровне посредством введения аппаратной избыточности за счёт включения запасных(резервных) элементов и связей, дополнительных по сравнению минимально необходимым для выполнения заданных функций в данных условиях работы. При общем резервировании резервируется вся система в целом. Общее резервирование в зависимости от способа включения резервных устройств можно разделить на постоянное резервирование и резервирование замещением, при котором резервные изделия замещают основные только после отказа. При общем постоянном резервировании резервные устройства подключены к основному в течение всего времени работы и находятся в одинаковом с ним режиме. Постоянное резервирование -к его преимуществам относится: относительная простота построения схем, отсутствие даже кратковременного перерыва в работе при отказе от одного до m-1 элементов системы, отсутствие дополнительных подключаемых элементов, снижающих общую надёжность схемы. Недостатки нагруженного резерва, кроме увеличения габаритов и массы системы –повышенный расход энергии, «старение» одновременно резервных элементов с основными элементами системы. При общем постоянном резервировании может использоваться только нагруженный резерв. Резервирование замещением – при резервировании замещением резервное устройство включается в работу системы при помощи автоматических устройств либо человеком-оператором вручную. При автоматическом включении требуется чрезвычайно высокая надёжность переключающих элементов. При большом количестве и невысокой надёжности этих дополнительных элементов, входящих в резервированную систему её надёжность может понизиться по сравнению с надёжностью нерезервируемой системы. Существует кратковременный перерыв, на время переключения на резервные устройства. При ручной замене отказавших элементов возрастает время переключения, но надёжность человека-оператора, производящего переключение, может быть принята в расчётах за единицу. При использовании нагруженного резерва запасные резервные элементы находятся в том же режиме работы, что и основные элементы(независимо от того, участвуют они в работе схемы или нет) и если при этом основной и резервный элемент идентичны, то интенсивности их отказов совпадают и надёжность основного и резервного устройств одинакова, и поэтому, если не учитывать надёжность автоматических переключающих устройств, характеристики надёжности рассчитываются по тем же формулам, что и для общего постоянного резервирования.

При использовании ненагруженного резерва, запасные резервные элементы до момента их включения в работу системы полностью отключены. В этом случае резервные устройства имеют самую высокую надёжность по сравнению с основными элементами, поэтому общее резервирование замещением с использованием ненагруженного резерва обеспечивают наилучшие показатели надёжности для случая общего резервирования.

Раздельное резервирование –при этом способе резервирования вводится индивидуальный резерв для каждой части неизбыточной системы.Раздельное резервирование бывает общим и замещением. При раздельном замещении отказ системы может произойти только тогда, когда отказ дважды подряд произойдёт в одном и том же устройстве(m=1), что маловероятно. Для оценки надёжности при раздельном резервировании используется сложный, специфический математический аппарат. В целом математический анализ показывает, что наиболее высокие показатели надёжности можно получить в случае построения систем с использованием раздельного резервирования замещением ненагруженным резервом.

Дата добавления: 2018-02-15; просмотров: 1491; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 59 60 61 62 636465 66 67 68 Следующая ⇒

Мы поможем в написании ваших работ!