Невозможен процесс, единственным результатом которого является передача теплоты.
Невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения одного тела.
Второй закон термодинамики определяет направление процессов, протекающих в замкнутых системах: для обратимых процессов - энтропия не изменяется, для необратимых - возрастает.
Видно, что dS и dQ имеют один и тот же знак. Это позволяет по характеру изменения энтропии судить о направлении процесса теплообмена. При нагревании тела dQ > 0 и энтропия возрастает (dS > 0), при охлажденииdQ < 0 и энтропия убывает (dS < 0). В обратимом адиабатном процессе dQ = 0, (dS = 0) и S = const.
Cуществует связь 2 закона термодинамики с молекулярно-кинетической теорией, согласно которой каждому состоянию молекулярной системы соответствует некоторое распределение ее молекул по объему и распределение молекул по скоростям.
Число всевозможных распределений молекул по объему (координатам) и скоростям, соответствующих данному термодинамическому состоянию называется термодинамической вероятностью состояния P тела или системы.
Между энтропией S и термодинамической вероятностью состояния P существует связь
S = k ln P . (4.39)
Термодинамическая вероятность состояния замкнутой системы при всех протекающих в ней процессах не может убывать. Это статистическое истолкование 2 закона термодинамики.
Возрастание энтропии означает, что любая система стремится в состояние с наибольшей вероятностью. Другими словами, наиболее вероятным состоянием системы является состояние полного хаоса.
Если применить этот термодинамический вывод к нашей Вселенной, то можно придти к заключению, что не смотря на ее огромные размеры, в ней тоже поздно или рано, но обязательно произойдет выравнивание концентрации материи; температура всех частей Вселенной также выровняется и наступит естественная «тепловая смерть» Вселенной.
В действительности такой вывод является несостоятельным по ряду причин. Так, например, до сих пор никто не доказал, что Вселенную можно рассматривать как замкнутую систему (вывод о возрастании энтропии получен в предположении о замкнутости рассматриваемой системы).Кроме того, из рассмотрения других функций состояния системы с большим количеством частиц следует, что возможны локальные отклонения в распределении плотности (у нас нет возможности провести такой вывод) материи, которые получили название флуктуаций. Флуктуации могут существовать достаточно долго, причем их среднее число не меняется с течением времени.
5.Поверхность жидкости
Поверхностное натяжение в жидкостях
Жидкое состояние вещества обязано своим существованием взаимодействию молекул между собой. Между молекулами действуют как силы притяжения, так и силы отталкивания. Природа этих сил электрическая, но они по разному зависят от расстояния: силы отталкивания оказываются более дальнодействующими. Как известно, жидкость имеет определенные границы, поэтому молекулы, находящиеся в пограничном слое, испытывают несколько другие воздействия по сравнению с молекулами, находящимися в «глубине» жидкости. «Глубинные» молекулы взаимодействуют со всеми окружающими их молекулами так, что равнодействующая всех сил для каждой «глубинной» молекулы оказывается равной нулю, тогда как на молекулы пограничного слоя действуют силы только с одной стороны мысленной сферы, описанной вокруг рассматриваемой молекулы. Появляется равнодействующая всех сил притяжения, направленная внутрь от границы. Наличие же сил отталкивания, которые тоже не компенсируются, приводит к тому, что расстояния между молекулами в пограничном слое несколько увеличиваются по сравнению с молекулами, находящимися внутри жидкости; в свою очередь, это приводит к тому, что энергия взаимодействия между молекулами также увеличивается. Таким образом, молекулы поверхностного слоя обладают добавочной потенциальной энергией Wпов ,величина которой зависит от площади поверхности, ограничивающей жидкость. Жидкость стремится к тому, чтобы по возможности уменьшить свою потенциальную энергию (это свойство присуще всем системам, обладающими потенциальной энергией), поэтому жидкость стремится приобрести форму шара, при условии, что на нее не действуют никакие внешние силы (например, сила тяжести), т.к. из всех геометрических тел определенного объема (массы) шар обладает наименьшей площадью ограничивающей его поверхностью. Хотя на молекулы пограничного слоя действуют силы, стремящиеся втянуть их вглубь жидкости, наблюдения за поверхностью жидкости показывают, что молекулы этого слоя могут достаточно долго оставаться на месте (вспомните пятна бензина и масла на поверхности луж). Это означает, что существуют еще какие-то силы, которые уравновешивают силы «втягивания». Эти силы назвали силами поверхностного натяжения потому, что они возникают в результате взаимодействия между собой молекул поверхностного слоя (см. рис. 5.1). При малейшем смещении какой-нибудь молекулы из поверхностного слоя вглубь жидкости возникает сила Fпов, направленная вверх, которая компенсирует Fвтяг. В пределе бесконечно малых смещений силы взаимодействия направлены по касательной к поверхности. Величина силы поверхностного натяжения зависит от природы жидкости и от протяженности поверхности, т.е. от ее длины l (cм. риc. 5.1).
Fпов = a l, (5.1)
                  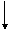       Fпов
Fнат Fнат граница
раздела
Fвтяг Fпов
Fнат Fнат граница
раздела
Fвтяг
      жидкость жидкость
    l
Рис. 5.1 Возникновение сил поверхностного натяжения l
Рис. 5.1 Возникновение сил поверхностного натяжения
|
где a - коэффициент поверхностного натяжения, характеризующий свойства жидкости. Из выражения (16.1) следует, что a представляет силу, действующую на единицу длины. Силы поверхностного натяжения стремятся сократить поверхность жидкости. Это приводит к тому, что при искривлении поверхности жидкости в ней возникает добавочное давление Dр , величина которого легко вычисляется. Для этого мысленно разрежем сферическую каплю жидкости по диаметру (рис. 5.2). Силы поверхностного натяжения действуют по касательной так, что на верхнюю полусферу действует результирующая сила, направленная вниз, а на нижнюю - направленная вверх. Величина этих сил одинакова и равна:
 , (5.2)
, (5.2)
где R - радиус капли, а 2pR - длина окружности, перпендикулярно которой действуют силы поверх ностного натяжения ( a на единицу длины).
                  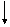                     
   2R
Рис. 5.2 Добавочное давление под изогнутой поверхностью 2R
Рис. 5.2 Добавочное давление под изогнутой поверхностью
|
Каждая из этих двух сил действует на площадь  , поэтому величина добавочного давления Dр равна:
, поэтому величина добавочного давления Dр равна:

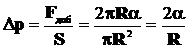 . (5.3)
. (5.3)
Это добавочное давление проявляется в так называемых капиллярных явлениях, когда уровень жидкости в очень узких трубках (капиллярах) поднимается (или опускается) относительно уровня жидкости в широкой части сосуда (см.рис. 5.3).
                                                                     2R
h
2R
h
 
  
  Рис. 5.3 Капиллярные явления. Рис. 5.3 Капиллярные явления.
|
Как видно из рис. 5.3, поведение жидкости в капилляре определяется формой мениска: при вогнутом мениске добавочное давление направлено вверх, и жидкость поднимается, а при выпуклом мениске добавочное давление направлено вниз, и жидкость опускается. Направление выпуклости мениска зависит от сравнительной силы взаимодействия между молекулами жидкости и жидкости и твердого тела, ограничивающего жидкость. Если взаимодействие жидкость - жидкость меньше, чем взаимодействие жидкость - твердое тело, то равнодействующая двух сил (см. рис. 5.4)Fрез направлена в сторону твердого тела. Молекулы жидкости, находящиеся вблизи границы раздела, сильнее при  тягиваются к твердому телу. В состоянии равновесия граница раздела располагается так, чтобы быть перпендикулярной результирующей силе. Жидкость как бы стремится подняться по поверхности твердого тела. В этом случае говорят, что наблюдается явление смачивания. Смачивание может полным и не полным. Степень смачивания определяетсякраевым углом
тягиваются к твердому телу. В состоянии равновесия граница раздела располагается так, чтобы быть перпендикулярной результирующей силе. Жидкость как бы стремится подняться по поверхности твердого тела. В этом случае говорят, что наблюдается явление смачивания. Смачивание может полным и не полным. Степень смачивания определяетсякраевым углом 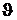 (см. рис. 5.4). Этот угол определяется как угол между касательной к поверхности жидкости и поверхностью твердого тела. При полном смачивании краевой угол стремится к нулю. Если же взаимодействие жидкость-твердое тело меньше, чем жидкость - жидкость, то результирующая сила направлена вовнутрь жид- кости (см. рис. 5.5), которая стремится образовать выпуклую поверхность.
(см. рис. 5.4). Этот угол определяется как угол между касательной к поверхности жидкости и поверхностью твердого тела. При полном смачивании краевой угол стремится к нулю. Если же взаимодействие жидкость-твердое тело меньше, чем жидкость - жидкость, то результирующая сила направлена вовнутрь жид- кости (см. рис. 5.5), которая стремится образовать выпуклую поверхность.

Fтж
Fжж Fрез
мениск J жидкости Рис. 16.4 Явление смачивания |
Молекулы, находящиеся вблизи границы раздела, как бы стремятся отойти от нее, - наблюдается явление несмачивания. Краевой угол в этом случае становится тупым. При полном несмачивании он равен p. При полном смачивании поверхность мениска становится полусферой (рис. 5.3). Сила добавочного давления Fдоб направлена вверх. Добавочное давление Dр уравновешивается гидростатическим давлением столба жидкости
Dр = rжgh.
   
    
J
Fтж
Fжж Fрез Рис. 5.5 Форма мениска при несмачивании |
Из выражения (5.3) следует, что высота подъема жидкости в капилляре равна
h =  . (5.4)
. (5.4)
При промежуточных значениях краевого угла 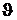 смачивание будут неполным. В этом случае радиус мениска R (см рис. 5.6.) связан с радиусом капилляра r:
смачивание будут неполным. В этом случае радиус мениска R (см рис. 5.6.) связан с радиусом капилляра r:
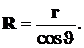 (5.5)
(5.5)
    Рис. 5.6 Подъем жидкости при неполном смачивании
Рис. 5.6 Подъем жидкости при неполном смачивании
|
Давление с выпуклой стороны мениска меньше, чем с вогнутой стороны на величину Dр, где
 , (5.6)
, (5.6)
поэтому высота подъема h жидкости в капилляре несколько меньше:
 . (5.7)
. (5.7)
При значениях краевого угла более 90о значения косинуса становятся отрицательными, что приводит к отрицательным значениям высоты подъема. 
Дата добавления: 2018-02-15; просмотров: 897; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!