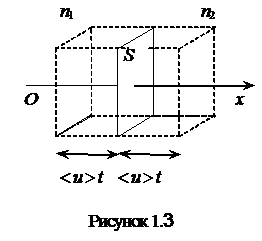Средняя длина свободного пробега молекул

⇐ ПредыдущаяСтр 3 из 7Следующая ⇒

Молекулы газа движутся хаотично, их траектории представляют собой ломаные линии из-за непрерывных соударений друг с другом. Путь, пройденный молекулами между двумя последовательными соударениями, называется длиной свободного пробега l. Длина свободного пробега меняется от соударения к соударению, поэтому вводится понятие средней длины свободного пробега < l >, как среднего пути, пройденного молекулой между двумя последовательными соударениями.

Для нахождения средней длины свободного пробега необходимо средний путь <L>, пройденный молекулой за некоторый промежуток времени t, разделить на среднее число соударений <Z> за это же время

<l> = или < l > = ,

где - средняя арифметическая скорость молекулы, <z> - среднее число соударений в единицу времени.

При движении со скоростью <u_отн> молекула будет сталкиваться со всеми молекулами газа, центры которых отстоят от траектории ее движения на расстояниях меньших или равных эффективному диаметру молекулы d (рис.1.2), т.е. со всеми молекулами, центры которых лежат внутри ломанного цилиндра длиной <u_отн>t и радиусом основания d.

Среднее число соударений молекулы в единицу времени

< z > = p d²n <u_отн>, (1.16)

где n - концентрация молекул, <u_отн> - средняя скорость движения молекул относительно друг друга (средняя относительная скорость).

Так как средняя относительная скорость <u_отн> связана со средней арифметической скоростью движения соотношением

<u_отн> = ,

то

< z > = p d²n (1.17)

< l > = . (1.18)

Выразив концентрацию n молекул из уравнения p = n k T,получим

< l > = 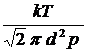. (1.19)

Явления переноса.

Хаотичность теплового движения молекул приводит к постоянному перемешиванию частиц, изменению их импульсов и энергий. Если в газе существует пространственная неоднородность плотности, температуры или скорости упорядоченного перемещения отдельных слоев газа, то хаотическое движение молекул со временем выравнивает эти неоднородности, т.е. в процессе хаотического теплового движения происходит перенос молекулами своих физических величин: массы, энергии или импульса. Механизм этих явлений одинаков и они носят название явлений переноса.

Исходя из представлений молекулярно-кинетической теории газов, получим общее уравнение для явлений переноса.

Рассмотрим некоторую площадку S, расположенную в газе (рис.1.3).

Так как молекулы газа движутся хаотично, то в направлении оси Ох будет двигаться только 1/6 часть всех молекул.

Двигаясь со средней арифметической скоростью через площадку S пройдут все молекулы, находящиеся в объемах t S слева (N₁) и справа (N₂) от площадки

N₁ = n₁ S t , N₂ = n₂ S t ,

где n₁, n₂- концентрация молекул слева и справа от площадки S.

Эти молекулы, перемещаясь через площадку S, переносят некоторую физическую величину j (массу, энергию, импульс).

Количество физической величины, переносимое молекулами в направлении оси Ox через площадку S за время t ,

N₁ j = (n₁ j) S t . (2.1)

Количество физической величины, переносимое в обратном направлении, через площадку S за время t ,

N₂ j = (n₂ j) S t .

Если рассматриваемый газ неоднороден по своим физическим характеристикам, то их перенос DN j через площадку S за время t равен

DN j = (n₁ j – n₂ j) S t . (2.2)

Перенос количества физической величины nj осуществляется при соударении молекул, поэтому значение физической величины j сохраняется неизменным на расстоянии < l > влево и вправо от площадки S. Поскольку < l > мало, то разность (n₁ j – n₂ j) можно представить в виде

n₁ j – n₂ j = – 2 < l > .

Тогда

D N j = – ( j ) < l > S t. (2.3)

Знак “–” показывает, что перенос физической величины происходит в направлении ее уменьшения.

Полученная формула называется уравнением переноса. На его основе рассмотрим явление переноса: диффузию, теплопроводность и внутреннее трение (вязкость) газов.

Диффузия газов

Диффузия- явление, заключающееся в самопроизвольном взаимном проникновении и перемешивании частиц газа. Диффузия возникает вследствие неодинаковой плотности в различных частях объема газа или различия в концентрациях в разных частях объема смеси газов. Диффузия заключается в переносе массы газа из области с большей концентрацией данного газа в область с меньшей концентрацией.

Рассмотрим некоторый объем газа (рис.1.4) с неоднородностью плотности, т.е. r₁ > r₂ ,

r₁ = n₁m , r₂ = n₂m.

Переносимой физической величиной j является масса m молекулы. Тогда уравнение переноса примет вид:

DN m = DM = – <l> S t = –< l > S t , (2.4)

где DM - масса газа, переносимая при диффузии за время t, через площадку S,перпендикулярно направлению убывания плотности r.

Обозначив <l> = D,

получим

DM = – D 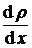S t . (2.5)

Полученная формула называется уравнением диффузии или законом Фика.

Коэффициент диффузии D зависит от сорта газа и его состояния (p, T).

Теплопроводность газов

Теплопроводность- явление выравнивания температур различных областей газа. Теплопроводность заключается в переносе энергии молекулами из более нагретых областей к более холодным.

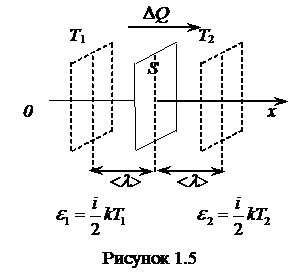
Рассмотрим некоторый объем газа (рис.1.5) с неоднородностью в отношении температуры (T₁> T₂).

Переносимой физической величиной является энергия молекул e . Так как наблюдается неоднородность по температуре, т.е. T₁>T₂, а

e₁= kT₁, e₂= kT₂, то e₁ > e₂ ,

где i - число степеней свободы молекулы газа.

Уравнение переноса переноса для теплопроводности можно записать:

DN kT = DQ , (2.6)

DQ = – ( ) < l > S t = –<l> n k ,

где DQ - количество теплоты, переносимое за счет теплопроводности за время t через площадку S, в направлении убывания температуры Т.

Обозначив <l> n k = c ,

получим

DQ = – c S t . (2.7)

Полученная формула называется уравнением теплопроводности или законом Фурье.

Коэффициент теплопроводности c не зависит от давления, если средняя длина свободного пробега меньше размеров сосуда.

Дата добавления: 2018-02-15; просмотров: 548; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!