Тема 1.3. Симплексный метод нахождения оптимального управленческого решения

Поиск и нахождение оптимального решения симплексным методом

Общая идея симплексного метода. Симплексные преобразования. Нахождение исходного опорного и оптимального решений. Анализ этапов принятия управленческого решения.

Примеры решения типовых задач

Пример 3. Найти исходное опорное решение ЗЛП.

Запишем задачу в канонической форме, вводя в левую часть первого неравенства системы ограничений дополнительную переменную 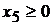со знаком «+», а в левую часть второго неравенства дополнительную переменную со знаком «минус».

Заполним симплексную таблицу 10 ( -строку не заполняем, пока система не будет приведена к единичному базису). Система уравнений имеет две базисные переменные и (столбцы и содержат единицу и нули), отмечаем это в столбце «Базис».

Таблица 10

Базис								с.о.
x₄ x₅	2 1 1	1 2 -1	-2 4 2	1 0 0	0 1 0	0 0 -1	24 22 10	12 22 10

Чтобы получить еще одну базисную переменную, обратимся к столбцам небазисных переменных , , , , из которых имеют положительные элементы первый, второй, третий столбцы. Выберем среди них, например, первый столбец – он и будет разрешающим.

Составим для положительных элементов разрешающего столбца симплексные отношения , , 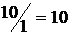(столбец с.о.). Наименьшему симплексному отношению (10) соответствует третья строка, которая и будетразрешающей строкой. На пересечении первого столбца и третьей строки находим разрешающий элемент . Проведем с ним одну итерацию метода исключения переменных.

Таблица 11

Базис
x₄ x₅ x₁	0 0 1	3 3 -1	-6 2 2	1 0 0	0 1 0	2 1 -1	4 12 10

В таблице 8 имеется теперь три базисные переменные , и . Это означает, что система приведена к единичному базису .

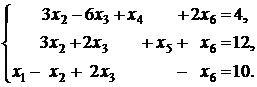
Приравняем к нулю свободные переменные , тогда базисные переменные будут равны свободным членам . Запишем исходное опорное решение .

Пример 4. Проверить, будет ли решение оптимальным. Если нет, то можно ли его улучшить.

Решение

Заполним -строку. Для этого вверху таблицы запишем коэффициенты при переменных и свободный член из целевой функции, слева от таблицы – коэффициенты при базисных переменных в целевой функции. В -строке под базисными переменными 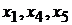запишем нули.

Таблица 12

		2	-3	6	1	0	0	0
	Базис								с. о.
1 0 2	x₄ x₅ x₁	0 0 1	3 3 -1	-6 2 2	1 0 0	0 1 0	2 1 -1	4 12 10

Вычислим оценки свободных переменных, значение целевой функции по и заполним таблицу 10:

Таблица 13

		2	-3	6	1	0	0	0
	Базис								с. о.
1 0 2	x₄ x₅ x₁	0 0 1	3 3 -1	-6 2 2	1 0 0	0 1 0	2 1 -1	4 12 10
		0	4	-8	0	0	0	24

Проверим, будет ли решение оптимальным. Из трех оценок свободных переменных в –строке , , одна оценка отрицательная - это - это признак того, что решение 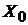не является оптимальным. Значение целевой функции для решения 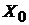находится в правом нижнем углу симплексной таблицы - это .

Теперь проверим, можно ли решение 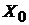улучшить: в –строке выберем отрицательную оценку , в столбце над которой имеются положительные элементы. Поэтому исходное опорное решение 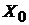можно улучшить.

Пример 5.Выполнить переход от решения 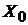к улучшенному решению и так далее до получения оптимального решения.

Решение

Рассмотрим симплексную таблицу 13, из которой следует решение 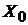. Для построения нового опорного решения нужно от базиса перейти к новому базису .

1. Выберем наибольшую по абсолютной величине отрицательную оценку , следовательно, столбец переменной 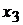станет разрешающим, а переменная 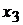должна быть введена в базис.

2. Для положительных элементов разрешающего столбца 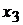составим симплексные отношения = 6; = 5 (столбец с.о.), выбираем наименьшее из них – это 5, оно находится в третьей строке, которая и станет разрешающей строкой. Значит, базисная переменная этой строки будет выведена из базиса и станет свободной. На пересечении разрешающих столбца и строки имеем разрешающий элемент .

3. Проведем в таблице итерацию симплексных преобразований с выбранным разрешающим элементом:

- разделим каждый элемент разрешающей строки на разрешающий элемент a₃₃= 2;

- в разрешающем столбце все элементы, кроме разрешающего элемента, заменим нулями;

- все остальные элементы таблицы, включая -строку, пересчитаем по правилу прямоугольника. Например, элемент 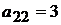в новой таблице получится равным . В результате получим симплексную таблицу 14.

Таблица 14

		2	-3	6	1	0	0	0
	Базис								с.о.
1 0 6		3 -1 1/2	0 4 -1/2	0 0 1	1 0 0	0 1 0	-1 2 -1/2	34 2 5	- 1 -
		4	3	0	0	0	- 4	64

4. Запишем новое опорное решение . В этом решении свободные переменные равны нулю: x₁= 0, x₂= 0, x₆= 0, а базисные – свободным членам: x₃= 5; x₄= 34; x₅= 2.

Значение целевой функции находится в правом нижнем углу симплексной таблицы: . Оно также проверяется путем подстановки компонент решения в целевую функцию .

5. Новое опорное решение «лучше» предыдущего опорного решения 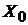, так как 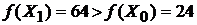. Вычислим двумя способами приращение целевой функции при переходе от 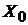к :

; .

Решение не является оптимальным, поскольку в строке оценок симплексной таблицы есть отрицательная оценка . Но можно улучшить, т.к. в столбце над этой оценкой имеется положительный элемент .

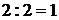6. Отрицательная оценка определяет переменную, вводимую в новый базис - это . Определим, какую переменную следует вывести из базиса . Составим симплексные отношения для положительных элементов столбца над отрицательной оценкой . Такое отношение является единственным и выполняется для второй строки, в которой базисной переменной является , она и выведется из базиса . Проведя итерацию симплексных преобразований с разрешающим элементом , получим симплексную таблицу 15 с базисом .

Таблица 15

2 -3 6 1 0 0 0

Базис с.о.

1 0 2 2,5 -0,5 0,25 2 2 0,5 0 0 1 1 0 0 0,5 0,5 0,25 0 1 0 35 1 5,5

2 11 0 0 2 0 68

Опорное решение «лучше» решения , так как . В -строке нет отрицательных оценок, поэтому решение оптимальное, а значение 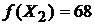- наибольшее.

Ответ: ; .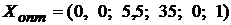

Дата добавления: 2018-02-15; просмотров: 828; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 Следующая ⇒

Мы поможем в написании ваших работ!