Графический метод нахождения оптимального решения экономических задач линейного программирования
Математическая модель, область допустимых решений, целевая функция. Поиск оптимального решения.Экономическая интерпретация.
Примеры решения типовых задач
Пример 2. Задача о рационе
Решить экономическую задачу линейного программирования графическим методом.
При составлении суточного рациона кормления скота можно использовать свежее сено не более 50 кг и силос не более 85 кг. Рацион должен содержать не менее 30 кормовых единиц, 1000 г белка, 100 г кальция и 80 г фосфора. Определить оптимальный рацион, исходя из условия минимума себестоимости.
В таблице 4 приведены данные о содержании указанных компонентов в 1 кг каждого корма и себестоимость этих кормов.
Таблица 7
|
Корм | Компоненты |
Себестоимость, ден. ед. | |||
| кормовые единицы | белок, г/кг | кальций, г/кг | фосфор, г/кг | ||
| Сено свежее, кг | 0,5 | 40 | 1,25 | 2 | 1,2 |
| Силос, кг | 0,5 | 10 | 2,5 | 1 | 0,8 |
Решение
Этап 1. Составление математической модели задачи.
Обозначим через 
и 
количество кг сена и силоса, которое предполагается включить в рацион. Естественно, что 
, 
. Из условия задачи следует, что 
(кг); 
(кг).
Количество кормовых единиц в рационе можно выразить суммой 
, что должно быть, по условию, не меньше 30: 
(ед.), или 
.
Ограничения по содержанию в рационе белка, кальция и фосфора имеют вид:
(г), или 
(для белка);
(г), или 
(для кальция);
(г) (для фосфора).
Себестоимость рациона в принятых обозначениях можно выразить формулой 
(руб.). Итак, математическая модель задачи построена.
|
|
|
Математическая постановка задачи: найти неотрицательные значения переменных и , которые удовлетворят системе линейных неравенств 
и при которых целевая функция принимает наименьшее значение 
.
Этап 2. Графическое решение стандартной ЗЛП.
Построим область допустимых решений задачи (рисунок 1). Для построения градиента увеличим координаты вектора 
в 50 раз, получим 
. Перпендикулярно градиенту построим одну из линий уровня.
| | 
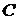
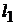
Рисунок 1 – Графическое решение задачи о рационе
Передвигая линию уровня в направлении градиента, найдем точку входа в область допустимых значений – это точка 
. Для нахождения координат этой точки решим систему уравнений прямых 
( ) и 
( ), пересекающихся в точке 
: 
. Получим 
.
|
|
|
В точке целевая функция принимает наименьшее значение, равное 
.
Этап 3. Анализ оптимального решения
Оптимальный рацион составляет 20 кг сена и 40 кг силоса, при этом себестоимость минимальная и составляет 56 ден. ед.
Подставив координаты оптимального решения 
в каждое неравенство, увидим, что третье и шестое неравенства обращаются в уравнения, а остальные – в строгие неравенства.
Это означает, что оптимальный рацион содержит необходимое количество кормовых единиц и фосфора, а белка и кальция – в избытке, причем сено и силос используются не в полном объеме.
Дата добавления: 2018-02-15; просмотров: 700; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!