Тема 1.2. Оптимизационные методы принятия управленческого решения в условиях определенности

Математические модели экономических задач линейного программирования

Примеры экономических ЗЛП, их математические модели.

Примеры решения типовых задач

Пример 1. Задача об использования сырья

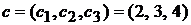Предприятие располагает двумя видами сырья S₁ и S₂ в количествах 10 и 15 условных единиц и изготавливает из него изделия трех видов П₁, П₂ и П₃. Известен расход каждого вида сырья на единицу продукции, что задается матрицей расхода сырья . Известна прибыль от реализации единицы продукции, которая задается вектором . Найти такой план производства продукции, от реализации которого предприятие получит максимальную прибыль.

Составить экономико-математическую модель задачи.

Решение

Для наглядности данные задачи занесем в таблицу.

Таблица 1 – Исходные данные задачи об использовании сырья

Вид сырья	Расход сырья на 1 единицу продукции			Запас сырья
Вид сырья	П₁	П₂	П₃	Запас сырья
S₁ S₂	1 4	2 3	3 2	10 15
Прибыль, ден. ед.	2	4	3

Построим экономико-математическую модель. Запишем искомый план производства в ви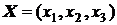де , где - количество единиц продукции П₁, П₂, П₃ соответственно. Система ограничений по расходу сырья примет вид

, , ,

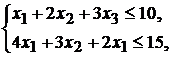
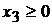а целевая функция (прибыли) .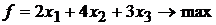

Математическая модель задачи имеет стандартную форму.

Задачи для самостоятельного решения

Задача 1. Составить математическую модель задачи.

Для изготовления изделий А и В используется 3 вида сырья. В таблице приведены нормы расхода сырья всех видов на изготовление единицы каждого вида изделий, запасы сырья и прибыль от реализации единицы продукции А и В.

Таблица 2

Сырье	А	В	Запасы сырья
S₁ S₂ S₃	16 8 5	4 7 9	784 552 567
Прибыль, ден. ед.	4	6

Задача 2. Составить математическую модель задачи.

На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки трех видов в количестве не менее 24, 30 и 30 штук. Каждый лист фанеры может быть разрезан на заготовки двумя способами. В таблице приведено количество получаемых заготовок и величины отходов, которые получаются при раскрое одного листа фанеры при каждом способе.

Сколько листов фанеры по каждому способу следует раскроить, чтобы получить минимальные отходы от раскроя?

Таблица 3

Вид заготовки	Количество заготовок при раскрое по способу:
	1	2
I II III	2 5 10	6 4 3
Отходы, кв. см	12	16

Указание. - количество листов фанеры, раскраиваемых по 1-му и 2-му способам. Ограничения по количеству заготовок - неравенства вида . Целевая функция - общие отходы от раскроя.

Задача 3. Составить математическую модель задачи.

На станках Р₁ и Р₂ производится два вида продукции А и В. Для изготовления 1 ед. продукции А станок Р₁ используется 2 часа, а станок Р₂ - 3 час. Для 1 ед. продукции В это время равно соответственно 1 час и 2 часа. Продукции А должно быть произведено не более 4 ед.

В течение суток станок Р₁ может работать не более 12 часов, а станок Р₂ - не более 5 часов. От реализации 1 ед. А прибыль составляет 2 ден. ед., а от 1 ед. В - 1 ден. ед. Какое количество продукции вида А и В нужно произвести, чтобы чистая прибыль была максимальной?

Указание. - количество продукции вида А (вида В). Целевая функция - это доход от реализации продукции.

Задача 4.Составить математическую модель задачи.

Доски длиной 4,5 м, имеющиеся в достаточном количестве, следует распилить на заготовки длиной 1,7 м и длиной 1,4 м, причем заготовок первого вида должно быть получено не менее 86 штук и заготовок второго вида - не менее 90 штук. Каждая доска может быть распилена на указанные заготовки несколькими способами.

1) Требуется найти число досок, распиливаемых каждым способом, с тем, чтобы наименьшее количество заготовок было получено:

1) из наименьшего числа досок; 2) при минимальных отходах.

Указание. Для составления математической модели задачи нужно сначала определить всевозможные способы распила на заготовки нужной длины и подсчитать остатки доски от раскроя по каждому способу раскроя.

Дополнительные задачи

Задача 1*. Составить математическую модель задачи.

Рассматривается пять проектов, которые могут быть осуществлены в течение последующих трех лет. Ожидаемые величины прибыли от реализации каждого из проектов и распределение необходимых капиталовложений по годам (в тыс. руб.) приводятся в таблице.

Таблица 4

Проект	Распределение капиталовложений			Прибыль
Проект	год 1	год 2	год 3	Прибыль
1	5	1	8	20
2	4	7	10	40
3	3	9	2	20
4	7	4	1	15
5	8	6	10	30
Максимальный объем капиталовложений	25	25	25

Требуется выбрать совокупность проектов, которой соответствует максимум суммарной прибыли.

Задача 2*. Составить математическую модель задачи.

Совет директоров фирмы изучает предложения по наращиванию производственных мощностей на трех принадлежащих фирме предприятиях. Для расширения всех трех предприятий фирма выделяет средства в объеме 5 млн. руб.

Каждое предприятие представляет на рассмотрение проекты, которые характеризуются величинами суммарных затрат (C) и доходов (R), связанных с реализацией каждого из проектов.

Соответствующие данные приведены в таблице, в которую включены также проекты с нулевыми затратами. Это позволяет учесть возможность отказаться от расширения какого-либо предприятия.

Таблица 5

Проект	Предприятие 1		Предприятие 2		Предприятие 3
Проект	С₁	R₁	С₂	R₂	C₃	R₃
1 2 3 4	0 1 2 -	0 5 6 -	0 2 3 4	0 8 9 12	0 1 - -	0 3 - -

Цель фирмы состоит в получении максимального дохода от инвестиций.

Задача 3*. Составить математическую модель задачи.

В задаче выбора вариантов примем, что для получения результата в виде максимально возможной прибыли необходимо два вида ресурсов: материальные и трудовые Возможны четыре варианта расхода ресурсов и получения прибыли (табл.).

Таблица 6

Показатели	Варианты				Наличие
Показатели	1	2	3	4
Прибыль, д.е./ед. Материальные ресурсы Трудовые ресурсы	65 200 10	80 180 15	90 240 22	210 250 28	– 800 50

Требуется выбрать, какие варианты принять для реализации при условии, чтобы общее число принятых вариантов не превышало трех.

Дата добавления: 2018-02-15; просмотров: 963; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!