Список дополнительной литературы. 9. Dupont Pascal, Vast Nicole
9. Dupont Pascal, Vast Nicole. Developpements limites.//Math.et.ped.-1997.-№114.-P.39-54.
10. Tong Jingcheng, Braza Peter A. A converse of the mean value theorem.//Amer.Math.Mon.-1997.-104; №10.-P.939-942.
Приложение 1.Перечень вопросов.
1. ЭКВИВАЛЕНТНЫЕ (РАВНОМОЩНЫЕ) МНОЖЕСТВА. СЧЕТНЫЕ МНОЖЕСТВА И ИХ СВОЙСТВА. СЧЕТНОСТЬ МНОЖЕСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ. НЕСЧЕТНОСТЬ МНОЖЕСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ.
Вводная часть
Эквивалентность множеств. Счетные множества. Примеры.
Раздел 1
Свойства счетных множеств. Счетность множества рациональных чисел.
Раздел 2
Теорема Кантора о несчетности отрезка [0,1]. Эквивалентность всех невырожденных промежутков. Понятие множества мощности континуума. Примеры. Мощность множества всех иррациональных чисел (всех трансцендентных чисел).
Раздел 3
Теорема Кантора-Бернштейна. Сравнение мощностей. Существование множеств сколь угодно высокой мощности.
Контрольные вопросы и задания
1. Приведите примеры множеств мощности гиперконтинуума.
2. Какова мощность множества H, если H —совокупность всех функций
f : R  R
R  (всех непрерывных функций f : R
(всех непрерывных функций f : R  R)?
R)?
3. Приведите определение Дедекинда бесконечного множества.
4. Существуют ли среди бесконечных множеств множества минимальной мощности?
5. Постройте биекцию интервала ( е,  ) на прямую R .
) на прямую R .
6. Приведите формулировку континуум-гипотезы.
2. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ, ЕГО ЕДИНСТВЕННОСТЬ. ТЕОРЕМА О ПРЕДЕЛЕ МОНОТОННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. ЧИСЛО е.
|
|
|
Вводная часть
Определение конечного предела числовой последовательности, геометрическая интерпретация определения. Пример сходящейся последовательности. Единственность конечного предела.
Раздел 1
Теорема Вейерштрасса о пределе монотонной последовательности (можно рассмотреть, например, случай возрастающей ограниченной сверху последовательности).
Раздел 2
Сходимость последовательности с общим членом  (n = 1,2, ...). Определение числа е.
(n = 1,2, ...). Определение числа е. 
Контрольные вопросы и задания
1.Является ли ограниченность последовательности необходимым условием (достаточным условием) существования конечного предела последовательности?
2.Существует ли предел последовательности с общим членом an , если
a) an= (-1)n (n = 1,2, ... ); b) an=  (n = 1,2, ... ).
(n = 1,2, ... ).
3.Является ли ограниченность сверху необходимым условием (достаточным условием) существования конечного предела возрастающей последовательности?
4.Исходя из определения бесконечного предела, докажите следующее равенство  .
.
5.Приведите представление числа е числовым рядом.
Укажем на два возможных подхода к построению ответа :
а) подробно освещается первый раздел, затем обзорно рассматривается вопрос сходимости последовательности с общим членом  и приводится определение числа е;
и приводится определение числа е;
|
|
|
b) приводится формулировка теоремы Вейерштрасса и подробно исследуется вопрос, относящийся к определению числа е.
3. ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ. РАЗЛИЧНЫЕ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА, ИХ ЭКВИВАЛЕНТНОСТЬ. СВОЙСТВА ПРЕДЕЛОВ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ. ОПЕРАЦИИ НАД НЕПРЕРЫВНЫМИ ФУНКЦИЯМИ.
Вводная часть.
Определения Коши и Гейне предела функции в точке. Геометрическая интерпретация. Определение непрерывности функции в точке. Примеры.
Раздел 1.
Единственность предела. Теоремы о пределе суммы, произведения и частного двух функций. Арифметические операции над непрерывными функциями.
Раздел 2.
Эквивалентность определений Коши и Гейне предела функции в точке.
Раздел 3.
Теоремы о предельном переходе в неравенствах. Примеры.
Контрольные вопросы и задания.
1.Существует ли: а)  ; б)
; б)  ?
?
2.Сформулируйте определение точки разрыва функции. Имеет ли точки разрыва непрерывная функция 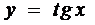 ?
?
3.Приведите классификацию точек разрыва функции.
4. Исходя из определения непрерывности, докажите непрерывность функции y=x. Покажите, что квадратичная функция непрерывна.
5.Сформулируйте аксиому выбора. Укажите хотя бы одну теорему из курса математического анализа, доказательство которой опирается на эту аксиому.
|
|
|
4. СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ.
Вводная часть.
Ограниченные функции. Верхняя (нижняя) грань функции.
Раздел 1.
Ограниченность непрерывной функции (первая теорема Вейерштрасса). Примеры и контрпримеры.
Достижимость экстремальных значений (вторая теорема Вейерштрасса).
Раздел 2.
Промежуточные значения непрерывной функции (первая и вторая теоремы Больцано-Коши). Следствия.
Контрольные вопросы и задания.
1.Докажите, что всякий многочлен нечетной степени хотя бы в одной точке обращается в нуль.
2.Является ли связным непрерывный образ промежутка?
3.Функция f определена и непрерывна на интервале. Существует ли наибольшее значение этой функции?
4.Функция f непрерывна и ограничена на интервале. Существует ли наибольшее значение этой функции?
5.Функция f задана на отрезке [a,b], причем f(a)·f(b)<0. Имеет ли эта функция хотя бы один нуль?
5. ОГРАНИЧЕННЫЕ И НЕОГРАНИЧЕННЫЕ ЧИСЛОВЫЕ МНОЖЕСТВА. ВЕРХНЯЯ И НИЖНЯЯ ГРАНИ МНОЖЕСТВА. ИХ СУЩЕСТВОВАНИЕ. ПРИНЦИП ВЛОЖЕННЫХ ОТРЕЗКОВ.
Вводная часть.
Ограниченное сверху (снизу) числовое множество. Верхняя (нижняя) грань множества. Примеры.
|
|
|
Раздел 1.
Теорема существования конечных точных границ ограниченного числового множества.
Раздел 2.
Принцип вложенных отрезков.
Контрольные вопросы и задания.
1.Будет ли справедливым утверждение, аналогичное принципу вложенных отрезков, для поля рациональных чисел?
2.Приведите пример ограниченного бесконечного числового множества (ограниченного открытого числового множества).
3. Сформулируйте принцип Архимеда.
4. Приведите свойство непрерывности поля действительных чисел.
5.Укажите некоторые арифметические свойства верхних и нижних граней.
6. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ ОСНОВНЫЕ СВОЙСТВА. РАЗЛОЖЕНИЕ В СТЕПЕННОЙ РЯД. НАТУРАЛЬНАЯ ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ. ЕЕ ОСНОВНЫЕ СВОЙСТВА. РАЗЛОЖЕНИЕ В СТЕПЕННОЙ РЯД.
Вводная часть.
Свойства степени ar , где a>0, rÎQ. Понятие степени ax для любого действительного числа x при а>0. Определение показательной функции, понятие логарифмической функции. Представление экспоненты y=ex (функции y=ln(1+x)) степенным рядом.
Раздел 1.
Определение степени ax ( a>0 ) при xÎR .Свойства показательной функции (область определения, непрерывность, производная , монотонность, пределы в бесконечно удаленных точках, множество значений, асимптота и график). Характеристическое свойство показательной функции.
Раздел 2.
Разложение экспоненты в ряд Тейлора по степеням x . Представление функции y=ln(1+x) степенным рядом на полуинтервале.
Раздел 3.
Определение логарифмической функции как обратной показательной. Свойства логарифмической функции (см. раздел 1).
Контрольные вопросы и задания.
1.Является ли показательная функция y=ax (a>0, a¹1) изоморфизмом группы ( R,+) в группу (R+ , · ) ?
2.Укажите решение задачи Коши:  , y(0)=1 .
, y(0)=1 .
3.При каком основании логарифмическая кривая y=logax пересекает ось Ox под углом 45°?
4.Разложите функцию  в ряд Маклорена. Проинтегрируйте полученный ряд на отрезке [0,x], где -1<x<1. Укажите сумму полученного ряда.
в ряд Маклорена. Проинтегрируйте полученный ряд на отрезке [0,x], где -1<x<1. Укажите сумму полученного ряда.
5.Исходя из определения предела, докажите равенство  .
.
7. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (СИНУС И КОСИНУС), ИХ СВОЙСТВА. СИНУС И КОСИНУС В КОМПЛЕКСНОЙ ОБЛАСТИ.
Вводная часть.
Определение функций синус и косинус в комплексной области. Основные свойства.
Раздел 1.
Функция синус в вещественной области. Непрерывность. Производная. Разложение в степенной ряд.
Определение функции синус в комплексной области. Формула Эйлера. Теорема сложения.
Раздел 2.
Определение функций синус и косинус в комплексной области. Производные. Формулы Эйлера. Теоремы сложения. Периодичность и нули функции синус. Функция синус в вещественной области.
Контрольные вопросы и задания.
1.Найдите Re sinz и |sinz|.
2. Докажите, что |sin z| может принимать сколь угодно большие значения.
3. Найдите алгебраическую форму следующего комплексного числа:
а) sin(1+i); б) sin(in), nÎN.
4.Является ли функция sin z (Ln z) целой?
5. Покажите, что функция sin z является аналитическим продолжением функции синус в комплексную область.
8. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ.
ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ТАБЛИЦА ПРОИЗВОДНЫХ.
ДИФФЕРЕНЦИАЛ. ЕГО СВЯЗЬ С ПРОИЗВОДНОЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.
Вводная часть.
Понятие производной функции одной вещественной переменной. Примеры вычисления производной по определению (y=sin x, y=ax, ...).
Таблица производных. Определение дифференцируемой функции.
Раздел 1.
Касательная к графику функции. Геометрический смысл производной. Механический смысл производной.
Раздел 2.
Производная суммы (произведения и частного).
Раздел 3.
Определение дифференциала функции одной вещественной переменной. Геометрический смысл. Связь производной и дифференциала. Необходимое условие дифференцируемости (теорема, контрпример).
Контрольные вопросы и задания.
1 Функция f определена и дифференцируема на отрезке [a,b]. Будет ли она непрерывна на отрезке? Является ли эта функция ограниченной?
2.Сформулируйте свойство инвариантности формы первого дифференциала.
3.Как найти производную степенно-показательного выражения xx (x>0) ?
4.Найдите производную функции  в точке x=0. Постройте график этой функции.
в точке x=0. Постройте график этой функции.
5.Укажите связь приращения функции, дифференциала функции и формулы Тейлора.
6.Найдите производную функции y=lnx, исходя из равенства 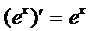 .
.
7.Найдите производную сложной функции y=arcsin 3x2.
При ответе на вопрос два раздела изложите подробно, а один раздел обзорно.
9.ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ.УСЛОВИЯ ПОСТОЯНСТВА И МОНОТОННОСТИ ФУНКЦИИ НА ПРОМЕЖУТКЕ.
Вводная часть.
Формула Лагранжа.
Раздел 1.
Теорема Лагранжа. Пример и контрпример. Геометрическая интерпретация формулы Лагранжа. Формула Коши.
Раздел 2.
Условия постоянства функции. Условия монотонности функции. Пример исследования функции на монотонность.
Контрольные вопросы и задания.
1.Приведите формулировку теоремы Ролля.
2.Всякая ли касательная к кривой имеет параллельную ей секущую? (Указание: рассмотрите функцию y=x3 на [-1;1] и касательную в точке (0;0).)
3. Найдите производную функции f(x) в точке x0, если 
4.Укажите ошибку в следующем "доказательстве" теоремы Коши: из равенств f(b)-f(a)=f¢(  )·(b-a) и g(b)-g(a)=g¢(
)·(b-a) и g(b)-g(a)=g¢(  )·(b-a) вытекает, что
)·(b-a) вытекает, что  .
.
5.Какую физическую интерпретацию формулы Лагранжа вы могли бы предложить?
6.Докажите, что  .
.
7.Исследуйте на монотонность функцию y=x-sin x. Приведите график.
10. ЭКСТРЕМУМЫ ФУНКЦИИ. УСЛОВИЯ ВЫПУКЛОСТИ НА ПРОМЕЖУТКЕ. ТОЧКИ ПЕРЕГИБА.
Вводная часть
Определение точки максимума (минимума) функции. Понятие выпуклой на интервале функции.
Раздел 1.
Необходимое условие экстремума. Контрпример. Достаточное условие строгого экстремума. Контрпримеры.
Раздел 2.
Критерий выпуклости. Достаточное условие строгой выпуклости. Контрпримеры.
Раздел 3.
Необходимое условие, выполняющееся в точке перегиба. Контрпример. Достаточные условия наличия точки перегиба.
Контрольные вопросы и задания.
1.Исследуйте на экстремум функцию y=x-x3. Постройте график функции.
2.Пусть определенная на отрезке [a,b] непрерывная функция f имеет лишь конечное число критических точек. Как найти наибольшее значение этой функции?
3.Какое определение выпуклости обычно используется в случае дифференцируемых функций?
4.Является ли точка x=0 точкой перегиба функции y=sin x? Постройте касательную в точке (0,0) к графику этой функции.
5.Приведите два различных определения точки перегиба дифференцируемой функции.
11.ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ИХ СВОЙСТВА. ИНТЕГРИРОВАНИЕ ПОДСТАНОВКОЙ И ПО ЧАСТЯМ. ПРИМЕРЫ.
Вводная часть.
Первообразная. Структура множества первообразных данной функции. Неопределенный интеграл. Примеры.
Раздел 1.
Свойства неопределенных интегралов. Таблица основных интегралов. Интегрирование по частям. Примеры.
Раздел 2.
Замена переменных в неопределенном интеграле. Примеры.
Контрольные вопросы.
1. Чем отличается равенство, содержащее неопределенный интеграл, от обычного равенства? Найдите ошибку в следующих рассуждениях:
 .
.
2. Как проверить результат интегрирования?
3. Сформулируйте достаточное условие существования первообразной. Существуют ли первообразные функций sin 2x и exp(-x2)?
4. Приведите примеры не выражающихся в конечном виде интегралов.
5. Вычислите интегралы:
а)  ; б)
; б)  ; в)
; в)  .
.
12. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. НЕОБХОДИМОЕ УСЛОВИЕ ИНТЕГРИРУЕМОСТИ. КРИТЕРИЙ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ. ИНТЕГРИРУЕМОСТЬ НЕПРЕРЫВНОЙ ФУНКЦИИ.
Вводная часть.
Задачи, приводящие к понятию определенного интеграла. Определенный интеграл. Пример вычисления интеграла по определению.
Раздел 1.
Необходимое условие интегрируемости функции. Контрпример.
Раздел 2.
Суммы Дарбу. Их свойства. Свойства определенных интегралов. Критерий интегрируемости функции.
Раздел 3.
Интегрируемость непрерывной функции.
Контрольные вопросы.
1. Укажите геометрический смысл определенного интеграла  , где f(x) – неотрицательная, непрерывная на [a,b] функция (например,
, где f(x) – неотрицательная, непрерывная на [a,b] функция (например,  , [a,b]=[-2,2]).
, [a,b]=[-2,2]).
2. Сформулируйте достаточные условия интегрируемости функции. Может ли разрывная функция быть интегрируемой?
3. Пусть f(x) интегрируема на [a,b]. Ее значения изменены в конечном числе точек. Будет ли новая функция интегрируемой?
При изложении ответа можно рассмотреть подробно первый или третий раздел и провести обзор вопросов второго раздела.
13. ИНТЕГРАЛ С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА.
Вводная часть.
Интеграл с переменным верхним пределом. Производная интеграла по верхнему пределу.
Раздел 1.
Непрерывность интеграла по верхнему пределу.
Раздел 2.
Дифференцируемость интеграла по верхнему пределу. Существование первообразной для непрерывной функции. Вид первообразной.
Раздел 3.
Основная теорема интегрального исчисления (формула Ньютона-Лейбница). Примеры.
Контрольные вопросы.
1. Сформулируйте достаточное условие существования первообразной функции. Существует ли первообразная функции а) 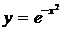 ; б) y=signx?
; б) y=signx?
2. Вычислите в точке х= –  первую и вторую производную функции:
первую и вторую производную функции:
а)  ; б)
; б)  ; в)
; в)  .
.
3. Запишите формулу интегрирование по частям в определенном интеграле и сформулируйте теорему о замене переменной в определенном интеграле.
Вычислите: а)  ; б)
; б)  .
.
Ответ можно построить следующим образом: подробно излагаются два раздела, оставшийся раздел рассматривается обзорно.
14. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА К ВЫЧИСЛЕНИЮ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ.
Вводная часть.
Квадрируемость. Вычисление площади криволинейной трапеции.
Раздел 1.
Верхняя и нижняя меры Жордана. Мера Жордана. Свойства измеримых множеств. Примеры.
Раздел 2.
Вычисление площадей фигур. Примеры.
Контрольные вопросы.
1.Проверьте с помощью определенного интеграла, что:
площадь круга  равна
равна  .
.
15.ЧИСЛОВЫЕ РЯДЫ. ОПРЕДЕЛЕНИЕ СХОДИМОСТИ ЧИСЛОВОГО РЯДА. КРИТЕРИЙ СХОДИМОСТИ ПОЛОЖИТЕЛЬНЫХ РЯДОВ. ТЕОРЕМЫ СРАВНЕНИЯ И ПРИЗНАКИ СХОДИМОСТИ ПОЛОЖИТЕЛЬНЫХ РЯДОВ. ПРИМЕРЫ.
Вводная часть.
Числовой ряд. Сумма ряда. Геометрический ряд, его сходимость. Необходимый признак сходимости ряда (доказательство). Контрпример.
Раздел 1.
Критерий сходимости положительных рядов. Теоремы сравнения. Примеры.
Раздел 2.
Признаки Даламбера и Коши сходимости положительных рядов. Примеры.
Контрольные вопросы.
1. Как влияет на сходимость ряда и его сумму удаление конечного числа членов ряда?
2. Докажите, что периодическая дробь 0,1(7) равна обыкновенной дроби  .
.
3. Сформулируйте интегральный признак сходимости ряда. Сходится ли ряд с общим членом na (n=1,2,...)?
4. Сходится ли ряд: а) 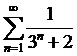 ; б)
; б)  ; в)
; в) 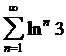 ?
?
16.АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ. ПРИЗНАКИ АБСОЛЮТНОЙ СХОДИМОСТИ. СВОЙСТВА АБСОЛЮТНО СХОДЯЩИХСЯ РЯДОВ. ТЕОРЕМА ЛЕЙБНИЦА. ПРИМЕРЫ.
Вводная часть.
Абсолютно сходящиеся ряды. Связь сходимости и абсолютной сходимости. Пример условно сходящегося ряда.
Раздел 1.
Переместительное свойство абсолютно сходящихся рядов. Теорема Римана. Теорема об умножении абсолютно сходящихся рядов.
Раздел 2.
Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда. Исследование сходимости ряда  .
.
Контрольные вопросы.
1. Сходится ли ряд  , если ряд
, если ряд  расходится ?
расходится ?
2. Приведите пример знакопеременного ряда, не являющегося знакочередующимся.
3. Сформулируйте признаки Даламбера и Коши абсолютной сходимости числового ряда.
4. Используя представление числа е–1 числовым рядом, вычислите приближенно значение е–1 с точностью до 0,01.
5. В сходящемся ряде  переставили члены ряда. Изменится ли сумма ряда?
переставили члены ряда. Изменится ли сумма ряда?
17.ФУНКЦИОНАЛЬНЫЕ РЯДЫ. ПОНЯТИЕ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНОГО РЯДА. СТЕПЕННЫЕ РЯДЫ В ДЕЙСТВИТЕЛЬНОЙ И КОМПЛЕКСНОЙ ОБЛАСТИ. ИНТЕРВАЛ И КРУГ СХОДИМОСТИ. СВОЙСТВА СТЕПЕННЫХ РЯДОВ.
Вводная часть.
Функциональные ряды. Примеры. Сходимость и равномерная сходимость функционального ряда. Степенные ряды.
Раздел 1.
Признак Вейерштрасса равномерной сходимости функционального ряда. Примеры.
Раздел 2.
Степенные ряды в действительной области. Лемма Абеля. Интервал и радиус сходимости. Формулировка теоремы Коши-Адамара. Степенные ряды в комплексной области.
Раздел 3.
Непрерывность суммы равномерно сходящегося функционального ряда. Непрерывность суммы степенного ряда.
Раздел 4.
Почленное интегрирование (дифференцирование) степенного ряда.
Контрольные вопросы.
1. Найдите сумму ряда:
а)  ; б)
; б)  ; в)
; в)  .
.
2. Найдите промежуток сходимости степенного ряда:
а)  ; б)
; б) 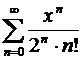 ; в)
; в)  .
.
3. Пусть Sn(x) и S(x) – частичная сумма и сумма ряда  соответственно. Sn(x) определены и непрерывны в R. Где определена и непрерывна сумма ряда S(x)?
соответственно. Sn(x) определены и непрерывны в R. Где определена и непрерывна сумма ряда S(x)?
4. Найдите производную суммы ряда  .
.
При изложении ответа на вопрос два раздела освещаются подробно, а остальные разделы обзорно.
18.ФОРМУЛА И РЯД ТЕЙЛОРА. УСЛОВИЯ РАЗЛОЖИМОСТИ ФУНКЦИИ В РЯД ТЕЙЛОРА. БИНОМИАЛЬНЫЙ РЯД.
Вводная часть.
Понятие формулы Тейлора. Многочлен Тейлора порядка n функции f в точке x0. Формальный ряд Тейлора.
Раздел 1.
Формула Тейлора с остаточным членом в форме Пеано. Формулы Маклорена для функций ex и sin x .
Раздел 2.
Формула Тейлора с остаточным членом в форме Лагранжа. Формула Маклорена с остаточным членом в форме Лагранжа для функции ex .
Раздел 3.
Достаточное условие разложимости функции в степенной ряд. Теорема о единственности представления функции степенным рядом по степеням x-x0. Биномиальный ряд.
Контрольные вопросы и задания.
1.Приведите примеры отыскания с помощью формулы Тейлора приближенного значения функции в точке. Вычислите предел 
2.Запишите формулу Тейлора для многочлена. Докажите, что многочлен, имеющий корень а, делится на двучлен х-а.
3. Пусть P(x)=x+x2 и  . Проверьте, что
. Проверьте, что  (x2) при x®0. Является ли Р(х) многочленом Тейлора порядка 2 функции f(x) в точке x0=0 ?
(x2) при x®0. Является ли Р(х) многочленом Тейлора порядка 2 функции f(x) в точке x0=0 ?
4. Приведите строгую формулировку следующего свойства: многочлен Тейлора является многочленом наилучшего приближения функции в окрестности точки.
5. С помощью формулы Тейлора вычислите число e с точностью до 0,001. 6.Разложите по формуле Маклорена функцию  на интервале (–1, 1).
на интервале (–1, 1).
19. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА. ПРИМЕРЫ. ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА. СХОДЯЩИЕСЯ И ФУНДАМЕНТАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК МЕТРИЧЕСКОГО ПРОСТРАНСТВА. ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА. ПРИНЦИП СЖИМАЮЩИХ ОТОБРАЖЕНИЙ, ЕГО ПРИМЕНЕНИЕ.
Вводная часть.
Понятие метрического пространства. Определение полного метрического пространства. Формулировка принципа сжимающих отображений.
Раздел 1.
Открытые и замкнутые множества в метрическом пространстве; их свойства. Фундаментальные последовательности. Полные метрические пространства. Примеры полных и неполных пространств (R, Rn, C[a,b], Q).
Раздел 2.
Сжимающие отображения. Непрерывность сжимающих отображений. Теорема Банаха о сжимающем отображении.
Раздел 3.
Некоторые применения принципа сжимающих отображений. (С помощью этого принципа доказать теорему существования и единственности решения задачи Коши для дифференциального уравнения первого порядка или теорему о неявной функции).
Контрольные вопросы.
1. Является ли отображение  метрикой, если
метрикой, если
а)  ;
;
б) 
2. Является ли открытым множество 
 , если
, если
а) X=(0,1); б) X=R ; в) X={2} ; г) X=[0,1) ?
Какие из этих множеств замкнуты?
3. Является ли метрическое пространство  полным, если
полным, если
а) M=(0,1) , 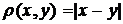 ; б) M=[0,1] ,
; б) M=[0,1] , 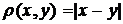 ?
?
4. Будет ли отображение  , заданное равенством
, заданное равенством  , сжимающим ?
, сжимающим ?
5. Сформулируйте теорему о пополнении метрического пространства.
20. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ. ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА.
Вводная часть.
Дифференциальное уравнение первого порядка. Решение дифференциального уравнения. Постановка задачи Коши для дифференциального уравнения первого порядка. Понятие частного решения. Формулировка теоремы существования и единственности решения задачи Коши для уравнения  .
.
Раздел 1.
Построение общего интеграла дифференциального уравнения с разделенными переменными. Теорема об общем интеграле дифференциального уравнения с разделяющимися переменными. Пример.
Раздел 2.
Линейные дифференциальные уравнения первого порядка. Построение общего решения линейного однородного дифференциального уравнения. Теорема об общем решении линейного неоднородного дифференциального уравнения. Пример.
Контрольные вопросы.
1. Укажите общее решение в области x>0, y>0 дифференциального уравнения  .
.
Является ли полупрямая x=0 (y>0) интегральной кривой этого уравнения?
2. Может ли решение уравнения  , где р(х)–непрерывная функция, принимать значения разных знаков ?
, где р(х)–непрерывная функция, принимать значения разных знаков ?
3. Покажите, что функции y1= –1 и  являются решениями уравнения
являются решениями уравнения 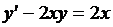 . Укажите общее решение этого уравнения.
. Укажите общее решение этого уравнения.
4. Найдите общее решение дифференциального уравнения  в области y>0. Покажите, что y=0 является его особым решением. Укажите решение, не являющееся ни частным, ни особым.
в области y>0. Покажите, что y=0 является его особым решением. Укажите решение, не являющееся ни частным, ни особым.
Ответ можно построить следующим образом: второй раздел освещается подробно, а первый раздел – обзорно.
21.ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ. ИХ ПРИМЕНЕНИЕ К ИЗУЧЕНИЮ СВОБОДНЫХ И ВЫНУЖДЕННЫХ КОЛЕБАНИЙ.
Вводная часть.
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Свойства решений, фундаментальная система решений, общее решение линейного однородного дифференциального уравнения. Линейное неоднородное дифференциальное уравнение. Структура общего решения. Уравнение вынужденных колебаний с периодической внешней силой. Явление резонанса.
Раздел 1.
Характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами. Фундаментальная система решений. Примеры.
Раздел 2.
Теорема о структуре общего решения линейного неоднородного дифференциального уравнения. Метод неопределенных коэффициентов нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами. Пример.
Раздел 3.
Уравнение свободных колебаний  .Общее решение уравнения.
.Общее решение уравнения.
Уравнение вынужденных колебаний с периодической внешней силой. Частное решение этого уравнения (в случае совпадения частот собственных и вынужденных колебаний). Явление резонанса.
Контрольные вопросы.
1. Является ли пара функций f(x) и g(x) линейно независимой, если:
а)  ;
;  ; б)
; б)  ;
;  ; в)
; в)  ;
;  .
.
2. Постройте общее решение уравнения: а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д) 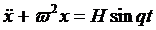 .
.
3. Выделите действительную и мнимую части комплекснозначной функции exp(ipx), xÎR.
4. Найдите удовлетворяющее условиям y(0)=1,  решение уравнения: а)
решение уравнения: а) 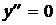 ; б)
; б)  ; в)
; в)  ; г)
; г) 
 .
.
22.ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. УСЛОВИЯ ДИФФЕРЕНЦИРУЕМОСТИ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ.
Вводная часть.
Понятие производной функции комплексной переменной. Условия Коши-Римана. Понятие аналитической функции. Правила дифференцирования. Примеры.
Контрольные вопросы.
1. Докажите, исходя из определения производной, что  .
.
2. Для функции f(z) укажите точки, в которых выполнены условия Коши-Римана:
а) 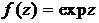 ; б)
; б)  .
.
3. Какие из следующих функций f(z) (zÎC) являются аналитическими:
а)  ; б)
; б)  ;в)
;в) 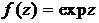 ;г)
;г)  ; д)
; д)  .
.
4. Пусть функции f и g дифференцируемы в точке z0ÎC. Докажите, что
а)  ; б)
; б)  .
.
Ответ может быть построен следующим образом:
1. Излагается доказательство критерия дифференцируемости функции, приводятся примеры дифференцируемых и не дифференцируемых в заданной точке функций, а также примеры аналитических функций.
2. Доказывается только необходимость или достаточность условий Коши-Римана. Тогда следует изложить также доказательство правил дифференцирования.
23. ФУНКЦИЯ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО. СВОЙСТВА ФУНКЦИИ: МОНОТОННОСТЬ, СИММЕТРИЧНОСТЬ, ПЕРИОДИЧНОСТЬ.
Вводная часть.
Отображение. Биекция. Понятие функции. Функция действительного переменного: область определения, множество значений, график, способы задания. Арифметические действия над функциями. Композиция функций. Обратная функция.
Раздел 1.
Монотонные и немонотонные функции. Промежутки монотонности. Монотонность композиции функций. Монотонность суммы двух функций. Достаточное условие обратимости функции. Монотонность обратной функции.
Раздел 2.
Четные и нечетные функции. Функции общего вида. Симметричность суммы и произведения двух функций. Симметричность функций, обратной к нечетной.
Раздел 3.
Периодические и непериодические функции. Период функции. Свойства периодических функций.
Контрольные вопросы.
1. Исследуйте монотонность произведения двух функций  , если
, если
а)  возрастает и положительна,
возрастает и положительна,  убывает и отрицательна;
убывает и отрицательна;
б)  и
и  возрастают и отрицательны.
возрастают и отрицательны.
2. Имеет ли четная функция обратную? Ответ обосновать.
3. Исследуйте симметрию композиции  , если
, если
а) 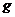 - четная;
- четная;
б) 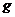 - нечетная,
- нечетная,  - четная;
- четная;
в)  и
и 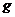 - нечетные.
- нечетные.
4. Является ли периодическая функция обратимой. Ответ обосновать.
5. Внутренняя функция композиции является периодической. Будет ли периодической композиция? Ответ обосновать.
6. Может ли периодическая функция быть: а) четной; б) нечетной; в) монотонной. Ответ обосновать.
Приложение 2. Критерии оценки ответа студента на государственном экзамене.
Оценка ”отлично” выставляется, если студент показал высокий уровень математической культуры, умение свободно ориентироваться в вопросах программы государственного экзамена, глубокое понимание проблем, идей и методов классических разделов математики, вынесенных на ГАИ, отвечает на вопросы правильно, свободно аргументирует свои ответы, выполняет все практические задания.
Оценка “хорошо” выставляется, если студент понимает суть заданных вопросов, но во время ответа допускает некоторые неточности, не имеющие принципиального значения.
Оценка “удовлетворительно” выставляется, если студент допустил достаточно большое число мелких неточностей, либо показал недостаточно глубокие, поверхностные знания по одному из вопросов билета, либо при ответе обнаружил существенные пробелы по одному – двум разделам программы, однако в целом обладает достаточным для будущей профессиональной деятельности и продолжения образования уровнем математической культуры.
Оценка “неудовлетворительно” выставляется, если студент не ответил на вопросы билета и при ответе на дополнительные вопросы не ориентируется в базовых понятиях.
Дата добавления: 2018-02-15; просмотров: 354; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
