Список дополнительной литературы. 10. Степанов Н.А., Культина Л.Ф
10. Степанов Н.А., Культина Л.Ф. Базовые требования к минимуму содержания и уровню подготовки студентов математического факультета по курсу «Геометрия» (Методические материалы). – Н.Новгород: НГПУ, 2000.
11. Агафонова Н.М., Репина Н.М. Методические указания по изучению темы «Векторные пространства и линейные операторы». – Н.Новгород: НГПУ, 1997.
Приложение 1.Перечень вопросов.
1.СКАЛЯРНОЕ, ВЕКОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЗАДАЧ ШКОЛЬНОГО КУРСА.
- Определение скалярного произведения и его свойства.
- Формулы для вычисления скалярного произведения, модуля вектора, угла между векторами в ортонормированном базисе.
- Определение векторного произведения векторов и его свойства. Геометрический смысл модуля векторного произведения. Критерий коллинеарности векторов.
- Вычисление координат векторного произведения в ортонормированном базисе. Свойства векторного произведения.
- Определение смешанного произведения векторов и его свойства.
- Критерий компланарности векторов. Геометрический смысл смешанного произведения.
- Свойства смешанного произведения векторов, вычисление смешанного произведения векторов в ортонормированном базисе.
- Приложения к решению задач.
2.УРАВНЕНИЕ ЛИНИИ. АЛГЕБРАИЧЕСКИЕ ЛИНИИ. МЕТОД КООРДИНАТ. ПРИЛОЖЕНИЕ МЕТОДА КООРДИНАТ К РЕШЕНИЮ ЗАДАЧ ШКОЛЬНОГО КУРСА ГЕОМЕТРИИ.
|
|
|
− Определение уравнения линии в данной системе координат. Параметрическое задание линии.
− Примеры и контрпримеры уравнения линии. Пример параметрического задания уравнения линии.
- Алгебраические линии. Порядок алгебраической линии. Основная теорема об алгебраических линиях.
- Прямая как алгебраическая линия первого порядка.
- Сущность метода координат.
Приложения к решению задач.
3.ЛИНИИ ВТОРОГО ПОРЯДКА. ЭЛЛИПС. ГИПЕРБОЛА. ПОРАБОЛА. УРАВНЕНИЯ И ОСНОВНЫЕ СВОЙСТВА ЛИНИЙ ВТОРОГО ПОРЯДКА. КОНИЧЕСКИЕ СЕЧЕНИЯ.
- Определение эллипса. вывод уравнения эллипса. Способ построения эллипса.
- Свойства эллипса. Эксцентриситет. Зависимость формы эллипса от эксцентриситета.
- Директрисы эллипса.
- Определение гиперболы. Уравнение гиперболы.
- Асимптоты гиперболы. Эксцентриситет и директрисы гиперболы.
- Парабола. Уравнение параболы.
- Линии второго порядка как конические сечения.
4. ГРУППА АФФИННЫХ ПРЕОБРАЗОВАНИЙ ПЛОСКОСТИ И ЕЕ ПОДГРУППЫ. ПРИЛОЖЕНИЯ АФФИННЫХ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ЗАДАЧ ШКОЛЬНОГО КУРСА ГЕОМЕТРИИ.
- Определение аффинного преобразования плоскости.
- Выражение аффинного преобразования в аффинной системе координат.
- Свойства аффинного преобразования.
|
|
|
- Группа аффинных преобразований плоскости и ее подгруппы.
- Подгруппы аффинной группы.
- Приложение аффинных преобразований к решению школьных задач.
5. ГРУППА ПРЕОБРАЗОВАНИЙ ПОДОБИЯ И ЕЕ ПОДГРУППЫ. ПРИЛОЖЕНИЯ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ К РЕШЕНИЮ ЗАДАЧ ШКОЛЬНОГО КУРСА.
- Определение преобразования подобия.
- Группа подобий плоскости.
- Теорема об инвариантности угла при подобии.
- Выражение преобразования подобия в координатах.
- Существование неподвижной точки.
- Гомотетия. Выражение гомотетии в координатах. Гомотетия как подобие, построение гомотетичных фигур.
- Движение. Теорема о представлении подобия композицией движения и гомотетии.
- Подгруппы группы подобий: группа движений, группа подобий первого рода, группа гомотетий с данным центром.
- Использование подобий в решении задач.
6. ГРУППА ДВИЖЕНИЙ ПЛОСКОСТИ. ЧАСТНЫЕ ВИДЫ ДВИЖЕНИЙ. ПРИЛОЖЕНИЕ ДВИЖЕНИЙ К РЕШЕНИЮ ЗАДАЧ ШКОЛЬНОГО КУРСА.
- Определение движений. Движение как частный случай подобия.
- Выражение движений в координатах.
- Критерий движения в терминах ортогональных матриц.
- Определение параллельного переноса, его выражение в координатах.
- Определение вращения, его выражение в координатах.
|
|
|
- Определение симметрии относительно точки, ее выражение в координатах.
- Определение симметрии относительно прямой, ее выражение в координатах.
- Определение скользящей симметрии, ее выражение в координатах.
- Параллельный перенос, вращение, симметрия как движения.
- Построение образов фигур при частных видах движений.
- Группа движений. Подгруппы группы движений: движения первого рода, группа параллельных переносов, группа вращений с заданным центром.
- Использование движений в решении задач.
7. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ.
- Расположение двух прямых в пространстве в зависимости от рангов матриц.
- Взаимное расположение прямой и плоскости (условие их параллельности, пересечения и принадлежности прямой плоскости).
- Взаимное расположение двух плоскостей в зависимости от рангов матриц.
- Доказательства обратных утверждений.
8.ПРОЕКТИВНАЯ ПЛОСКОСТЬ И ЕЕ МОДЕЛИ. СВОЙСТВА ПРОЕКТИВНОЙ ПЛОСКОСТИ.
- Определение проективного пространства. Размерность проективного пространства. Плоскость.
- Понятие модели проективной плоскости.
- Связка прямых трехмерного аффинного пространства как модель проективной плоскости.
|
|
|
- Фактор-пространство V*3 по отношению коллинеарности как модель Р2.
- Сфера с отождествленными диаметрально противоположными точками как модель проективной плоскости. Полусфера с отождествленными диаметрально противоположными точками граничной окружности.
- Расширенная аффинная плоскость.
- Пересечение прямых на проективной плоскости.
- Замкнутость прямых на проективной плоскости.
- Неразделяемость на 2 части проективной плоскости прямой.
- Невозможность определения «лежать между» для трех точек проективной плоскости.
- Компактность.
9.ПРЕОБРАЗОВАНИЯ ПРОЕКТИВНОЙ ПЛОСКОСТИ. ГРУППА ПРОЕКТИВНЫХ ПРЕОБРАЗОВАНИЙ. ПРИЛОЖЕНИЕ ПРОЕКТИВНЫХ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ЗАДАЧ ШКОЛЬНОГО КУРСА.
- Определение проективного преобразования плоскости.
- Выражение проективного преобразования в проективных координатах.
- Группа проективных преобразований плоскости.
- Инвариантность понятия прямой при проективном преобразовании.
- Теорема о неподвижной точке проективного преобразования.
- Теорема о неподвижной прямой.
- Гомология проективной плоскости. Построение гомологичных точек.
- Гомология расширенной аффинной плоскости.
- Использование проективных преобразований в решении задач.
10.ИЗОБРАЖЕНИЕ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ФИГУР В ПАРАЛЛЕЛЬНОЙ ПРОЕКЦИИ.
- Понятие параллельного проектирования.
- Понятие изображения по методу параллельного проектирования.
- Изображение плоских фигур в параллельной проекции. Теорема об изображении треугольника. Теорема о построении изображения точки по изображению треугольника.
- Изображение четырехугольника, трапеции, параллелограмма, п-угольника.
- Изображение правильного шестиугольника.
- Изображение окружности.
- Теорема Польке-Шварца.
- Изображение тетраэдра, пирамиды, призмы.
- Изображение цилиндра.
- Изображение конуса.
- Изображение шара.
- Изображение сечений многогранников плоскостями.
11.СИСТЕМА АКСИОМ ВЕЙЛЯ ТРЕХМЕРНОГО ЕВКЛИДОВА ПРОСТРАНСТВА. НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМЫ АКСИОМ ВЕЙЛЯ.
- Основные понятия и основные отношения в схеме Вейля.
- Система аксиом Вейля.
- Непротиворечивость аксиоматики Вейля (построение модели).
- Определение прямой и плоскости в схеме Вейля.
- Основные теоремы о прямых и плоскостях в схеме Вейля.
12.СИСТЕМА АКСИОМ ГИЛЬБЕРТА ЕВКЛИДОВА ПРОСТРАНСТВА (ОБЗОР).
- Подход Гильберта к построению аксиоматической теории.
- Основные понятия и основные отношения аксиоматики Гильберта.
- Аксиомы принадлежности, порядка, конгруэнтности, параллельности и непрерывности в аксиоматике Гильберта.
- Некоторые следствия из аксиом.
- Метод доказательства содержательной непротиворечивости евклидовой геометрии.
13.АКСИОМЫ ПЛОСКОСТИ ЛОБАЧЕВСКОГО. НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМЫ АКСИОМ ПЛОСКОСТИ ЛОБАЧЕВСКОГО.
- Аксиомы абсолютной геометрии в схеме Гильберта.
- Аксиома Лобачевского.
- Модель плоскости Лобачевского. Интерпретация основных понятий и отношений аксиоматики плоскости Лобачевского в схеме Гильберта.
- Непротиворечивость планиметрии Лобачевского. Модель Пуанкаре. Модель Кели – Клейна.
- Доказательство аксиом Гильберта и аксиомы Лобачевского в модели.
- Непротиворечивость планиметрии Лобачевского в схеме Гильберта.
14.ТИПЫ ПРЯМЫХ В ПЛОСКОСТИ ЛОБАЧЕВСКОГО. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ И РАСХОДЯЩИХСЯ ПРЯМЫХ.
- Определение параллельных и расходящихся прямых в плоскости Лобачевского.
- Отношение параллельности на множестве всех направленных прямых есть отношение эквивалентности.
- Поведение расстояния от точки, движущейся по прямой, до параллельной ей прямой.
- Отсутствие общего перпендикуляра у параллельных прямых.
- Расходимость двух перпендикуляров к одной прямой.
- Существование и единственность общего перпендикуляра к двум расходящимся прямым.
- Поведение расстояния от точки, движущейся по прямой, до расходящейся с ней прямой.
15.ГЛАДКИЕ ЛИНИИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ. ФОРМУЛЫ ФРЕНЕ.
- Определение кривой в трехмерном евклидовом пространстве.
- Примеры кривых.
- Касательный вектор кривой. Регулярные и бирегулярные кривые.
- Натуральная параметризация кривой.
- Прямые и плоскости, связанные с точкой гладкой кривой.
- Репер Френе.
- Формулы Френе.
- Критерий обращения кривизны и кручения в нуль.
16.ГЛАДКИЕ ПОВЕРХНОСТИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ И ЕЕ ПРИЛОЖЕНИЯ.
- Определение гладкой поверхности в Е3, параметризация поверхности.
- Гладкие поверхности класса Ск.
- Примеры поверхностей в Е3 .
- Нормаль и касательная плоскость к поверхности.
- Первая квадратичная форма поверхности.
- Длина кривой на поверхности.
- Угол между кривыми на поверхности. Критерий ортогональности координатной сети на поверхности.
- Площадь области поверхности.
Дисциплины «МАТЕМАТИЧЕСКИЙ АНАЛИЗ», «ТФДП», «ТФКП», «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»
1. Эквивалентные (равномощные) множества. Счетные множества и их свойства. Счетность множества рациональных чисел. Несчетность множества действительных чисел.
2. Предел числовой последовательности, его единственность. Теорема о пределе монотонной последовательности. Число 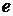 .
.
3. Предел функции в точке. Различные определения предела, их эквивалентность. Свойства пределов. Непрерывность функции в точке. Операции над непрерывными функциями.
4. Свойства функций, непрерывных на отрезке.
5. Ограниченные и неограниченные числовые множества. Верхняя и нижняя грани множества. Их существование. Принцип вложенных отрезков.
6. Показательная функция, ее основные свойства. Разложение в степенной ряд. Натуральная логарифмическая функция. Ее основные свойства. Разложение в степенной ряд.
7. Тригонометрические функции (синус и косинус), их свойства. Синус и косинус в комплексной области.
8. Дифференцирование функций одной переменной. Геометрический и механический смысл производной. Правила дифференцирования. Таблица производных. Дифференциал. Его связь с производной и геометрический смысл.
9. Основные теоремы дифференциального исчисления. Условия постоянства и монотонности функции на промежутке.
10. Экстремумы функции. Условия выпуклости на промежутке. Точки перегиба.
11. Первообразная и неопределенный интеграл. Их свойства. Интегрирование подстановкой и по частям. Примеры.
12. Определенный интеграл. Необходимое условие интегрируемости. Критерий интегрируемости функции. Интегрируемость непрерывной функции.
13. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
14. Площадь плоской фигуры. Приложения определенного интеграла к вычислению площади плоской фигуры.
15. Числовые ряды. Определение сходимости числового ряда. Критерий сходимости положительных рядов. Теоремы сравнения и признаки сходимости положительных рядов. Примеры.
16. Абсолютно и условно сходящиеся ряды. Признаки абсолютной сходимости. Свойства абсолютно сходящихся рядов. Теорема Лейбница. Примеры.
17. Функциональные ряды. Понятие равномерной сходимости функционального ряда. Степенные ряды в действительной и комплексной области. Интервал и круг сходимости. Свойства степенных рядов.
18. Формула и ряд Тейлора. Условия разложимости функции в ряд Тейлора. Биномиальный ряд.
19. Метрические пространства. Примеры. Открытые и замкнутые множества. Сходящиеся и фундаментальные последовательности точек метрического пространства. Полные метрические пространства. Принцип сжимающих отображений, его применение.
20. Обыкновенные дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными. Линейные уравнения первого порядка.
21. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Их применение к изучению свободных и вынужденных колебаний.
22. Производная функции комплексного переменного. Условия дифференцируемости. Правила дифференцирования. Понятие аналитической функции.
23. Функция действительного переменного. Свойства функции: монотонность, симметричность, периодичность.
Список основной литературы
1. Кудрявцев Л.Д. Курс математического анализа: в 3–х томах.–М.: Высшая школа, 1988. Т.1,2
2. Кудрявцев Л.Д. Курс математического анализа.: в 3–х томах..–М.: Высшая школа, 1989. Т.3
3. Маркушевич А.И. Краткий курс теории аналитических функций.-М.: Физматгиз, 1961.
4. Маркушевич А.И., Маркушевич Л.А. Введение в теорию аналитических функций.-М.: Просвещение, 1977.
5. Матвеев Н.М. Дифференциальные уравнения.-Л.: ЛГУ, 1963.
6. Натансон И.П. Теория функций вещественной переменной.- М.: Наука, 1974.
7. Райков Д.А. Одномерный математический анализ.-М.: Высшая школа, 1982.
8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: в 3–х томах.-М.: Наука, 1966. Т.1,2.
Дата добавления: 2018-02-15; просмотров: 399; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
