Список дополнительной литературы. ГОУ ВПО «Нижегородский государственный педагогический университет»
ГОУ ВПО «Нижегородский государственный педагогический университет»
Министерство образования и науки Российской федерации
Федеральное агентство по образованию
Факультет математики, информатики и физики
Кафедры математического анализа, алгебры и геометрии
ПРОГРАММА И ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ИТОГОВОЙ ГОСУДАРСТВЕННОЙ АТТЕСТАЦИИ СТУДЕНТОВ ПО СПЕЦИАЛЬНОСТЯМ «МАТЕМАТИКА» И «МАТЕМАТИКА С ДОПОЛНИТЕЛЬНОЙ СПЕЦИАЛЬНОСТЬЮ»
(очная и заочная формы обучения)
Содержание:
1. Программа и оценочные средства (приложения №№ 1-3) для государственного экзамена по основной специальности «Математика» (очная форма обучения).
2. Материалы по защите дипломных работ (очная форма обучения).
3. Содержание государственного экзамена по специальности «Математика» (заочная форма обучения).
Н.Новгород
2010
ГОУ ВПО «Нижегородский государственный педагогический университет»
Министерство образования и науки Российской федерации
Федеральное агентство по образованию
Факультет математики, информатики и физики
Кафедры математического анализа, алгебры и геометрии
П Р О Г Р А М М А
государственного экзамена
по основной специальности
Специальность «Математика с дополнительной специальностью»
(очная форма обучения)
СОСТАВИТЕЛИ: Программа утверждена на
|
|
|
Доцент кафедры алгебры и геометрии Совете математического факультета
______________ Н.А. Степанов от ________ ____г., протокол № ___.
Доцент кафедры алгебры и геометрии
______________ В.И. Грачева
Доцент кафедры математического анализа
______________ Р.Г. Рахманкулов Декан математического факультета
профессор _________Е.Н. Перевощикова
Н.Новгород
2010
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Целью государственных аттестационных испытаний по математике является проверка математической подготовленности выпускников математического факультета в соответствии с требованиями к содержанию и уровню предметной подготовки, отраженными в ГОС ВПО.
|
|
|
В задачи государственной аттестации входит:
¯ проверка глубины и прочности овладения испытуемыми основами математики;
¯ установление уровня математического развития выпускников, уровня их математической культуры.
Программа содержит наиболее важные темы, раскрывающие принципы математического анализа, вопросы, связанные с изучением основных алгебраических структур, а также аксиоматику и аналитические методы в геометрии. Включенное в программу госэкзамена содержание разделов математического анализа, алгебры и геометрии определяет фундаментальную основу подготовки выпускника по дисциплинам предметного блока, является базовым для школьного курса математики и соответсвует требованиям ГОС ВПО.
Экзаменующиеся должны:
¯ владеть системой основных алгебраических и теоретико-числовых понятий, сознавать их фундаментальный и прикладной характер, понимать их роль и место в системе математических дисциплин; знать основные факты теории важнейших алгебраических структур (групп, колец, полей, векторных пространств), теорию колец многочленов, теорию сравнений и показателей чисел в кольце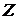 
; уметь находить решение системы линейных алгебраических уравнений, применять теорию сравнений к исследованию теоретико-числовых задач, определять тип и свойства бинарных отношений;
|
|
|
¯ знать аксиоматический метод построения геометрии, аксиоматику школьного курса геометрии и геометрии Лобачевского, иметь ясное представление о различных группах преобразований плоскости и уметь пользоваться этими преобразованиями при решении задач; владеть векторным и координатным методами исследования геометрии плоскости и пространства; знать основы теории изображения плоских и пространственных фигур в параллельной проекции, основные свойства линий и поверхностей в евклидовом пространстве;
¯ владеть основными понятиями теории пределов, непрерывности, производной и дифференциала, первообразной и определенного интеграла, теории рядов и теории множеств; владеть техникой дифференцирования и интегрирования, уметь исследовать сходимость числовых рядов и находить решения простейших дифференциальных уравнений; знать основные свойства элементарных аналитических функций.
Формой госаттестации по математике является междисциплинарный экзамен, проводимый по билетам. Билеты состоят из двух теоретических вопросов, один из которых выбирается из списка вопросов цикла дисциплин ТФДП, ТФКП, МАТЕМАТИЧЕСКИЙ АНАЛИЗ и ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, второй выбирается из списка вопросов цикла дисциплин АЛГЕБРА, ТЕОРИЯ ЧИСЕЛ и ГЕОМЕТРИЯ.
|
|
|
На экзамене студентам могут быть предложены дополнительные вопросы из разделов программы, не охваченных билетом.
Содержание государственного экзамена
Дисциплина «АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ»
1. Векторные пространства. Линейно зависимая и линейно независимая системы векторов. Базис и размерность векторного пространства. Изоморфизм конечномерных векторных пространств.
2. Матрица. Ранг матрицы. Обратная матрица. Полная линейная группа.
3. Система линейных уравнений, критерий их совместности и определенности, методы решения. Однородная система линейных уравнений, фундаментальная система решений.
4. Группа. Подгруппа. Нормальный делитель группы. Фактор-группа.
5. Кольцо. Область целостности. Поле. Подкольцо. Идеалы кольца. Фактор-кольцо.
6. Основные типы колец и связь между ними.
7. Линейный оператор. Матрица линейного оператора. Образ, ядро, ранг, дефект линейного оператора. Критерий обратимости линейного оператора. Диагонализируемость линейного оператора.
8. Простые и составные числа. Бесконечность множества простых чисел в натуральном ряду. Факториальность кольца Z.
9. Сравнения в Z, их свойства. Полная и приведенная системы вычетов. Линейные сравнения с одной переменной.
10. Показатели, их свойства. Обращение обыкновенной дроби в десятичную и определение длины периода десятичной дроби. Приложение теории сравнений к выводу признаков делимости.
11. Многочлены над полем F. Евклидовость кольца F[x]. НОД и НОК многочленов, алгоритм Евклида. Разложение многочлена в произведение неприводимых множителей.
12. Многочлены над С, R, Q. Рациональные корни целочисленного многочлена.
13. Строение простого алгебраического расширения поля. Освобождение от алгебраической иррациональности в знаменателе дроби.
14. Построение кольца многочленов от нескольких переменных над полем F. Симметрические многочлены. Основная теорема о симметрических многочленах.
15. Функция Эйлера, ее свойства. Теоремы Эйлера и Ферма.
16. Цепные дроби. Существование и единственность цепной дроби. Представление действительных чисел цепными дробями.
Список основной литературы
1. Сизый С.В. Лекции по теории чисел. – М.: Физматлит, 2007.
2. Агафонова Н.М., Грачева В.И., Коленова Е.М. Теория многочленов от одной и нескольких переменных: Учебное пособие. – Н.Новгород: НГПУ, 2008.
3. Агафонова Н.М., Коленова Е.М. Линейные операторы векторных пространств. Н.Новгород: НГПУ, 2009.
4. Бухштаб А.А. Теория чисел. – СПб.: Изд-во «Лань», 2008.
5. Типы колец: Методические рекомендации по курсу «Алгебра». – Н.Новгород: НГПУ, 2004.
6. Теория групп: Методические рекомендации по курсу «Алгебра». – Н.Новгород: НГПУ, 2004.
7. Базовые требования к минимуму содержания и уровню подготовки студентов математического факультета по курсу «Алгебра»: Методические материалы. – Н.Новгород: НГПУ, 2003.
8. Алгебраические структуры с одной и двумя бинарными операциями: Учебно-методическое пособие/ Н.М.Агафонова и др. – Н.Новгород: НГПУ, 2005.
9. Глухов М.М. Алгебра: Учеб. для студентов вузов, обучающихся по группе спец. В области информационной безопасности: В 2 т. – М.: Гелиос АРВ, 2003.
10. Винберг Э.Б. Курс алгебры – М.: Факториал Пресс, 2002.
11. Методические указания по изучению темы «Теория групп и колец». – Н.Новгород: НГПИ им. Горького, 1990.
12. Куликов Л.Я. Алгебра и теория чисел. – М.: Высшая школа, 1979.
Список дополнительной литературы
13. Кострикин А.И. Введение в алгебру.: Учеб. для студ. ун-та, обучающихся по специальности «Математика» и «Прикладная математика»: В 2 т. – М.: Физ.-мат. лит., 2000.
14. Куликов Л.Я., Маскаленко А.И., Фомин А.А. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физико-математических специальностей пединститутов. – М.: Просвещение, 1993.
15. Методические указания по изучению темы «Системы линейных уравнений». – Горький: ГГПИ им. Горького, 1988.
16. Проскуряков И.В. Сборник задач по линейной алгебре. – 7-е изд. – М.: Наука. Главн. ред. физ.-мат. лит-ры, 1984.
17. Методические указания по изучению темы «Теория многочленов». – Н.Новгород: НГПИ им. Горького, 1992.
18. Методические указания по изучению темы «Теория делимости и теория сравнений». – Н.Новгород: НГПУ, 1995.
Приложение 1.Перечень вопросов.
1. ВЕКТОРНЫЕ ПРОСТРАНСТВА. ЛЕНЕЙНО ЗАВИСИМАЯ И ЛИНЕЙНО НЕЗАВИСИМАЯ СИСТЕМЫ ВЕКТОРОВ. БАЗИС И РАЗМЕРНОСТЬ ВЕКТОРНОГО ПРОСТРАНСТВА. ИЗОМОРФИЗМ КОНЕЧНОМЕРНЫХ ВЕКТОРНЫХ ПРОСТРАНСТВ.
- Определение векторного пространства. Примеры векторных пространств. Простейшие свойства векторных пространств.
- Понятие линейной комбинации системы векторов. Определения линейно зависимой и линейно независимой систем векторов. Основные свойства линейно зависимой системы векторов (доказать некоторые свойства).
- Понятие базиса конечномерного векторного пространства. Теорема о существовании базиса ненулевого конечномерного векторного пространства. Примеры. Понятие размерности векторного пространства (корректность определения).
- Координаты вектора в данном базисе, их свойства.
- Определение изоморфизма векторных пространств, критерий изоморфизма конечномерных векторных пространств. Примеры изоморфных векторных пространств.
2. МАТРИЦА. РАНГ МАТРИЦЫ. ОБРАТНАЯ МАТРИЦА. ПОЛНАЯ ЛИНЕЙНАЯ ГРУППА.
- Понятие прямоугольной матрицы. Задание на множестве матриц данного порядка структуры векторного пространства. Правило умножения матриц подходящих порядков.
- Ранг матрицы. Совпадение строчечного и столбцового рангов матрицы. Элементарные преобразования над матрицами. Ступенчатые матрицы. Способ нахождения ранга матрицы. Примеры.
- Квадратные матрицы. Единичная матрица. Вырожденная и невырожденная квадратные матрицы. Критерий вырожденности матрицы. Примеры.
- Понятие матрицы, обратной данной невырожденной матрице. Способы нахождения матрицы, обратной данной.
- Обоснование того, что множество невырожденных квадратных матриц одного и того же порядка образует мультипликативную группу. Понятие полной линейной группы.
3. СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ, КРИТЕРИЙ ИХ СОВМЕСТНОСТИ И ОПРЕДЕЛЕННОСТИ, МЕТОДЫ РЕШЕНИЯ. ОДНОРОДНАЯ СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ, ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ.
- Понятие линейного уравнения, его решения. Понятие системы линейных уравнений, ее решения. Различные формы записи системы линейных уравнений.
- Совместность системы линейных уравнений. Критерий совместности системы линейных уравнений. Примеры.
- Определенность совместной системы линейных уравнений. Критерий определенности системы. Примеры.
- Описание различных методов решения систем линейных уравнений (метод Гаусса, метод Крамера, матричный метод). Иллюстрация методов на примерах.
- Однородная система линейных уравнений, пространство ее решений. Базис пространства решений однородной системы линейных уравнений (фундаментальная система решений).
- Способ нахождения фундаментальной системы решений однородной системы линейных уравнений.
4. ГРУППА. ПОДГРУППА. НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ ГРУППЫ. ФАКТОР-ГРУППА.
- Определение группы. Простейшие свойства групп. Примеры групп. Абелева группа.
- Понятие подгруппы данной группы. Критерии подгруппы (обосновать один из них). Примеры.
- Сравнение элементов группы по подгруппе. Левые и правые классы смежности. Понятие нормального делителя.
- Критерий нормального делителя группы. Примеры нормальных делителей.
- Построение фактор-группы данной группы по ее нормальному делителю. Примеры фактор-групп.
5. КОЛЬЦО. ОБЛАСТЬ ЦЕЛОСТНОСТИ. ПОЛЕ. ПОДКОЛЬЦО. ИДЕАЛЫ КОЛЬЦА. ФАКТОР-КОЛЬЦО.
- Определение и примеры колец.
- Делители нуля в кольце. Область целостности.
- Определение подкольца. Критерий подкольца.
- Обратимые элементы кольца. Мультипликативная группа кольца.
- Поле. Примеры полей.
- Идеал кольца. Построение фактор-кольца по идеалу. Корректность операций в фактор-кольце.
- Кольцо классов вычетов как пример фактор-кольца.
6. ОСНОВНЫЕ ТИПЫ КОЛЕЦ И СВЯЗЬ МЕЖДУ НИМИ.
- Простые, составные, обратимые элементы кольца.
- Факториальные кольца. Факториальность кольца Z.
- Главные идеалы в кольце. Кольца главных идеалов. Примеры. Теорема о возрастающей цепочке идеалов в кольце главных идеалов.
- Факториальность кольца главных идеалов.
- Евклидовы кольца. Деление с остатком в кольце. НОД и НОК в евклидовом кольце.
- Доказать, что евклидово кольцо является кольцом главных идеалов.
7. ЛИНЕЙНЫЙ ОПЕРАТОР. МАТРИЦА ЛИНЕЙНОГО ОПЕРАТОРА. ОБРАЗ, ЯДРО, РАНГ, ДЕФЕКТ ЛИНЕЙНОГО ОПЕРАТОРА. КРИТЕРИЙ ОБРАТИМОСТИ ЛИНЕЙНОГО ОПЕРАТОРА.
- Определение и примеры линейного оператора векторного пространства V.
- Матрица линейного оператора в данном базисе, правило ее нахождения.
- Образ, ядро линейного оператора как подпространства пространства V.
- Ранг и дефект линейного оператора. Теорема о сумме ранга и дефекта.
- Обратимые линейные операторы. Критерий обратимости линейного оператора.
8. МНОГОЧЛЕНЫ НАД ПОЛЕМ F. ЕВКЛИДОВОСТЬ КОЛЬЦА F[X]. НОД И НОК МНОГОЧЛЕНОВ, АЛГОРИТМ ЕВКЛИДА. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА В ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ МНОЖИТЕЛЕЙ.
- Понятие многочлена от одной переменной над полем F. Степень многочлена.
- Сложение и умножение многочленов. Кольцо многочленов F[x].
- Определение деления с остатком в кольце F[x]. Теорема о евклидовости кольца F[x].
- Определение НОД и НОК многочленов. Связь между ними.
- Нахождение НОД и НОК многочленов. Алгоритм Евклида.
- Неприводимые многочлены над полем F. Разложение многочлена в произведение неприводимых множителей.
9. МНОГОЧЛЕНЫ НАД C,R,Q. РАЦИОНАЛЬНЫЕ КОРНИ ЦЕЛОЧИСЛЕННОГО МНОГОЧЛЕНА.
- Алгебраическая замкнутость поля С (основная теорема алгебры).
- Неприводимые многочлены над полем С.
- Неприводимые многочлены над полем R.
- Свойства комплексных корней многочлена с действительными коэффициентами.
- Критерий Эйзенштейна неприводимости над Q многочлена с целыми коэффициентами.
- Алгоритм нахождения рациональных корней многочлена с целыми коэффициентами.
10. СТРОЕНИЕ ПРОСТОГО АЛГЕБРАИЧЕСКОГО РАСШИРЕНИЯ ПОЛЯ. ОСВОБОЖДЕНИЕ ОТ АЛГЕБРАИЧЕСКОЙ РАЦИОНАЛЬНОСТИ В ЗНАМЕНАТЕЛЕ ДРОБИ.
- Понятие алгебраического числа над числовым полем. Примеры.
- Минимальный многочлен алгебраического числа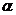 
, его свойства.
- Понятие расширения поля F. Простое алгебраическое расширение поля F с помощью алгебраического числа 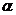(поле F( 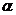)). Его строение.
- Освобождение от алгебраической иррациональности в знаменателе дроби. Примеры.
11. ПОСТРОЕНИЕ КОЛЬЦА МНОГОЧЛЕНОВ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ НАД ПОЛЕМ F. СИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ. ОСНОВНАЯ ТЕОРЕМА И СИММЕТРИЧЕСКИХ МНОГОЧЛЕНАХ.
- Понятие кольца многочленов от нескольких переменных над полем F, его строение.
- Степень многочлена от нескольких переменных.
- Лексикографическая запись многочлена от нескольких переменных.
- Действие подстановкой 
на многочлен. Симметрический многочлен.
- Основные симметрические многочлены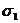 
, …, 
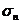. Основная теорема о симметрических многочленах. Примеры ее применения.
- Теорема Виета для алгебраически замкнутого поля.
12. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА. БЕСКОНЕЧНОСТЬ МНОЖЕСТВА ПРОСТЫХ ЧИСЕЛ В НАТУРАЛЬНОМ РЯДУ. ФАКТОРИАЛЬНОСТЬ КОЛЬЦА Z.
- Понятие простого и составного числа. Элементарные свойства простых чисел.
- Критерий составного (простого) числа, его использование при исследовании натурального числа на простоту.
- «Решето» Эратосфена как способ отбора простых чисел.
- Доказательство теоремы Евклида о бесконечности множества простых чисел во множестве натуральных чисел.
- Простые и составные элементы во множестве целых чисел, их свойства. Понятие факториального кольца.
13. СРАВНЕНИЯ В Z, ИХ СВОЙСТВА. ПОЛНАЯ И ПРИВЕДЕННАЯ СИСТЕМЫ ВЫЧЕТОВ. ЛИНЕЙНЫЕ СРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ.
- Сравнимость целых чисел по натуральному модулю.
- Основные свойства числовых сравнений (обосновать некоторые из них).
- Строение классов вычетов по данному модулю. Классы вычетов, взаимно простые с модулем. Кольцо классов вычетов.
- Понятие полной и приведенной систем вычетов по данному модулю, их свойства. Примеры.
- Общий вид сравнения первой степени с одной переменной, разрешимость такого сравнения.
- Различные методы решения линейных сравнений с одной переменной, примеры. Обоснование некоторых методов решения линейных сравнений.
14. ПОКАЗАТЕЛИ, ИХ СВОЙСТВА. ОБРАЩЕНИЕ ОБЫКНОВЕННОЙ ДРОБИ В ДЕСЯТИЧНУЮ И ОПРЕДЕЛЕНИЕ ДЛИНЫ ПЕРИОДА ДЕСЯТИЧНОЙ ДРОБИ. ПРИЛОЖЕНИЕ
- Понятие показателя данного целого числа по данному модулю. Примеры. Основные свойства показателей чисел по данному модулю.
- Обращение обыкновенной дроби в десятичную, способ выяснения характера полученной десятичной дроби (конечная, бесконечная, чисто периодическая или смешанная периодическая). Примеры.
- Использование понятия показателя числа для нахождения длины периода бесконечной десятичной дроби.
- Понятие признака делимости натурального числа на заданное число.
- Использование понятия показателя числа при выведении признаков делимости на числа, взаимно простые с модулем. Признаки делимости на 3,9,11.
- Общий признак (признак Паскаля) делимости и его использование. Примеры.
15. ФУНКЦИЯ ЭЙЛЕРА, ЕЕ СВОЙСТВА. ТЕОРЕМЫ ЭЙЛЕРА И ФЕРМА.
- Определение функции Эйлера, ее мультипликативность.
- Формула для вычисления функции Эйлера. Примеры.
- Теорема Ферма. Теорема Эйлера, ее обоснование.
- Примеры использования теоремы Эйлера в решении сравнений с переменной и в решении других задач теории сравнений.
16. ЦЕПНЫЕ ДРОБИ. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ ЦЕПНОЙ ДРОБИ. ПРЕДСТАВЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ ЦЕПНЫМИ ДРОБЯМИ.
- Понятие конечной цепной дроби. Примеры.
- Теорема о возможности представления произвольного рационального числа в виде цепной дроби.
- Единственность представления рационального числа в виде цепной дроби.
- Подходящие дроби, их основные свойства. Роль подходящих дробей при нахождении приближенных значений данного числа.
Дисциплина «ГЕОМЕТРИЯ»
1. Скалярное, векторное и смешанное произведение векторов. Приложения к решению задач школьного курса геометрии.
2. Уравнение линии. Алгебраические линии. Метод координат. Приложение метода координат к решению задач школьного курса геометрии.
3. Линии второго порядка. Эллипс, гипербола, парабола. Уравнения и основные свойства линий второго порядка. Конические сечения.
4. Группа аффинных преобразований плоскости и ее подгруппы. Приложение аффинных преобразований к решению задач школьного курса геометрии.
5. Группа преобразований подобия и ее подгруппы. Приложение преобразований подобия к решению задач школьного курса геометрии.
6. Группа движений плоскости. Частные виды движений. Приложение движений плоскости к решению задач школьного курса геометрии.
7. Взаимное расположение двух прямых, прямой и плоскости, двух плоскостей в пространстве.
8. Проективная плоскость и ее модели. Свойства проективной плоскости.
9. Преобразование проективной плоскости. Группа проективных преобразований. Приложение проективных преобразований к решению задач школьного курса геометрии.
10. Изображение плоских и пространственных фигур в параллельной проекции.
11. Система аксиом Вейля трехмерного евклидова пространства. Непротиворечивость системы аксиом Вейля.
12. Система аксиом Гильберта евклидова пространства (обзор).
13. Аксиомы плоскости Лобачевского. Непротиворечивость системы аксиом плоскости Лобачевского.
14. Типы прямых в плоскости Лобачевского. Взаимное расположение параллельных и расходящихся прямых в плоскости Лобачевского.
15. Гладкие линии в евклидовом пространстве. Сопровождающий трехгранник пространственной кривой. Формулы Френе.
16. Гладкие поверхности в евклидовом пространстве. Первая квадратичная форма поверхности и ее приложения.
Список основной литературы
1. Степанов Н.А., Жогова Т.Б., Казнина О.В. Геометрия I, II: Учеб. пособие для студентов физико-математических факультетов пед.вузов. – Н.Новгород: НГПУ, 2007.
2. Степанов Н.А. Элементы общей топологии: Учебно-методическое пособие. – Н.Новгород: НГПУ, 2006.
3. Степанов Н.А., Культина Л.Ф. Изображение плоских и пространственных фигур. Методическое пособие по геометрии.- Н.Новгород: НГПУ, 2003.(присвоен гриф УМО) 4. 4. Степанов Н.А. Преобразования плоскости: Методическое пособие для проведения практических занятий.- Н.Новгород: НГПУ, 2003.
5. Степанов Н.А., Культина Л.Ф. Базовые требования к минимуму содержания и уровню подготовки студентов математических факультетов по курсу «Геометрия»: Методические материалы. – Н.Новгород: НГПУ, 2002.
6. Пыжьянова А.Н. Материалы по геометрии: каноническая теория кривых второго порядка. Методические разработки для студентов математического факультета.- Н.Новгород: НГПУ,2002. (присвоен гриф УМО)
7. Степанов Н.А., Культина Л.Ф. Модели геометрических систем (расчетно-графическая работа по курсу «Геометрия»).- Н.Новгород: НГПУ, 2002.
8. Казнина О.В., Антонова С.Е. Материалы по геометрии: Элементы векторной алгебры. Методические разработки для студентов математического факультета. – Н.Новгород: НГПУ, 2002.
9. Никитина Г.Н. Каноническая теория кривых второго порядка: Методические материалы для студентов 1-ого курса математического факультета. – Н.Новгород: НГПУ, 2002.
Дата добавления: 2018-02-15; просмотров: 1139; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!