Задачи для контрольной работы. Исследовать функцию и построить эскиз ее графика
Исследовать функцию и построить эскиз ее графика
1. 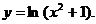 10.
10.  18.
18. 
2. 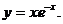 11.
11. 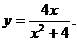 19.
19. 
3.  12.
12. 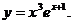 20.
20. 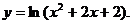
4. 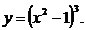 13.
13. 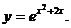 21.
21. 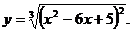
5. 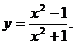 14.
14. 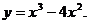 22.
22. 
6. 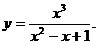 15.
15.  23.
23. 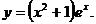
7.  16.
16.  24.
24. 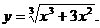
8. 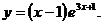 17.
17. 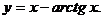 25.
25. 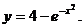
9. 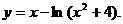
Нахождение наибольшего и наименьшего значения функции
1.5.1. Наибольшее и наименьшее значения функции на отрезке.
Непрерывная на некотором отрезке  функция
функция 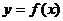 , как известно, принимает на этом отрезке свои наибольшее и наименьшее значения, соответственно, М и т. Эти значения могут достигаться либо в точках экстремумов, либо на концах отрезка. Следовательно, алгоритм поиска наибольшего и наименьшего значений функции
, как известно, принимает на этом отрезке свои наибольшее и наименьшее значения, соответственно, М и т. Эти значения могут достигаться либо в точках экстремумов, либо на концах отрезка. Следовательно, алгоритм поиска наибольшего и наименьшего значений функции 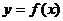 состоит в следующем.
состоит в следующем.
1. Найти производную функции  .
.
2. Найти критические точки первой производной, расположенные внутри отрезка  (если они имеются; экстремумы функции могут быть только в этих точках).
(если они имеются; экстремумы функции могут быть только в этих точках).
3. Вычислить значения функции в найденных критических точках и на концах отрезка (т.е. в точках 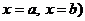 .
.
4. Среди найденных значений функции выбрать наибольшее и наименьшее.
Пример. Найти наибольшее и наименьшее значения функции 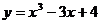 на отрезке
на отрезке  .
.
Решение. Следуя изложенному алгоритму, находим 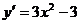 . Теперь определяем критические точки:
. Теперь определяем критические точки:  , т.е.
, т.е. 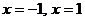 . Среди них только первая точка лежит на заданном отрезке. Остается вычислить значения функции в точке
. Среди них только первая точка лежит на заданном отрезке. Остается вычислить значения функции в точке  и на концах отрезка. Имеем:
и на концах отрезка. Имеем: 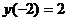 ,
, 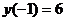 ,
, 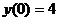 . Теперь среди найденных значений выбираем наибольшее и наименьшее:
. Теперь среди найденных значений выбираем наибольшее и наименьшее: 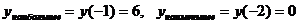 .
.
|
|
|
Задачи о наибольших и наименьших значениях величин
Многие задачи из геометрии, физики и других областей естествознания могут быть представлены следующей моделью: имеется некоторая величина, зависящая от двух переменных 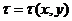 ; требуется найти ее наибольшее или наименьшее значение при условии, что х и у связаны некоторым уравнением.
; требуется найти ее наибольшее или наименьшее значение при условии, что х и у связаны некоторым уравнением.
Обычно удается выразить одну переменную через другую, в результате чего величина 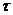 оказывается функцией одной переменной. Для нахождения ее наибольшего или наименьшего значений остается применить вышеизложенный алгоритм.
оказывается функцией одной переменной. Для нахождения ее наибольшего или наименьшего значений остается применить вышеизложенный алгоритм.
Пример. Прямоугольный треугольник имеет периметр, равный 2а. Найти размеры его катетов, при которых он обладает наибольшей площадью.
Решение. Если х и у – катеты треугольника, то, как известно из геометрии, его площадь 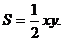 Очевидно, что каждый катет меньше периметра, т.е.
Очевидно, что каждый катет меньше периметра, т.е. 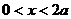 ,
, 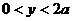 . На основании теоремы Пифагора имеем гипотенузу
. На основании теоремы Пифагора имеем гипотенузу 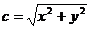 , так что теперь периметр треугольника
, так что теперь периметр треугольника 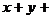
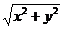 =2а. Выразим из полученного уравнения у через х, после чего получим S в виде функции одной переменной. Итак, выполняем соответствующие преобразования полученного уравнения:
=2а. Выразим из полученного уравнения у через х, после чего получим S в виде функции одной переменной. Итак, выполняем соответствующие преобразования полученного уравнения:
|
|
|
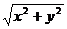 =
=  ;
;
 ;
;
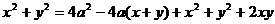 ;
;
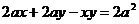 .
.
Теперь 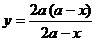 и
и 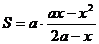 , при этом
, при этом 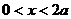 . В полученном интервале значений х наибольшее значение площади S может быть достигнуто в точке максимума; следовательно, исследуем знаки первой производной
. В полученном интервале значений х наибольшее значение площади S может быть достигнуто в точке максимума; следовательно, исследуем знаки первой производной
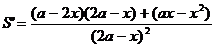 или
или 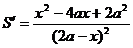 .
.
Критические точки определяем из условия 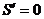 (знаменатель дроби при
(знаменатель дроби при 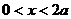 будет строго положительным):
будет строго положительным):
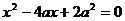 , откуда
, откуда  .
.
Ясно, что  , поэтому на интервале (0, 2а) остается единственная критическая точка
, поэтому на интервале (0, 2а) остается единственная критическая точка 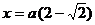 , при переходе через которую производная
, при переходе через которую производная 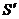 меняет свой знак с «+» на «-». Следовательно, в этой единственной точке максимума площадь треугольника и принимает свое наибольшее значение. При этом
меняет свой знак с «+» на «-». Следовательно, в этой единственной точке максимума площадь треугольника и принимает свое наибольшее значение. При этом 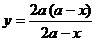 =
= 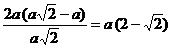 .
.
Итак, при заданном периметре, равном 2а наибольшая площадь прямоугольного треугольника достигается, если он равнобедренный с катетами 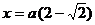 ,
, 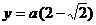 .
.
Дата добавления: 2018-02-15; просмотров: 394; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
