Задачи для контрольной работы. 1.2Найти производную функции (в п.б функция у(х) задана параметрически) :
1.2Найти производную функции  (в п.б функция у(х) задана параметрически) :
(в п.б функция у(х) задана параметрически) :
1. а)  ; б)
; б) 
2. а)  ; б)
; б) 
3. а)  б)
б) 
4. а)  ; б)
; б) 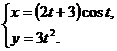
5. а)  ; б)
; б) 
6. а)  ; б)
; б) 
7. а)  ; б)
; б) 
8. а)  ; б)
; б) 
9. а)  ; б)
; б) 
10. а)  ; б)
; б) 
11. а)  ; б)
; б) 
12. а)  ; б)
; б) 
13. а)  б)
б) 
14. а)  б)
б) 
15. а)  б)
б) 
16. а)  б)
б) 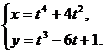
17. а)  б)
б) 
18. а)  б)
б) 
19. а)  б)
б) 
20. а) 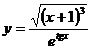 б)
б) 
21. а)  б)
б) 
22. а)  б)
б) 
23. а)  б)
б) 
24. а)  б)
б) 
25. а)  б)
б) 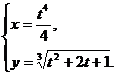
Касательная и нормаль. Правило Лопиталя
1.3.1. Касательная к графику функции (кривой)  , проведенная в точке
, проведенная в точке  , имеет уравнение
, имеет уравнение

Нормаль, к графику функции (кривой) 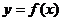 , проведенная в точке
, проведенная в точке  (т.е. перпендикуляр к касательной в точке касания) в том случае, если
(т.е. перпендикуляр к касательной в точке касания) в том случае, если  имеет уравнение
имеет уравнение

Пример. Составить уравнения касательной и нормали к кривой, заданной уравнением  , в точке
, в точке  .
.
Решение. В нашем случае точка касания имеет (по условию задачи) координаты 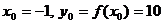 . Вычислим
. Вычислим  тогда
тогда  . Уравнение
. Уравнение  или
или 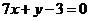 является уравнением касательной, а уравнение
является уравнением касательной, а уравнение  или
или  есть уравнение нормали к заданной кривой в указанной точке.
есть уравнение нормали к заданной кривой в указанной точке.
|
|
|
Задачи для контрольной работы
1.3.1. Составить уравнение касательной и нормали к кривой, заданной уравнением 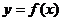 , в точке
, в точке  :
:
1.  14.
14. 
2.  15.
15. 
3.  16.
16. 
4. 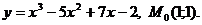 17.
17. 
5.  18.
18. 
6.  19.
19. 
7.  20.
20. 
8.  21.
21. 
9.  22.
22. 
10. 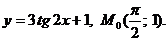 23.
23. 
11.  24.
24. 
12.  25.
25. 
13. 
1.3.2. Правило Лопиталя раскрытия неопределенностей вида  и
и  состоит в следующем: если существует предел вида
состоит в следующем: если существует предел вида  , то
, то
 =
=  .
.
Здесь а – некоторая точка или бесконечность любого знака.
Если отношение производных при  снова есть неопределенность указанного выше вида, то правило можно применить снова, переходя ко вторым производным и т.д.
снова есть неопределенность указанного выше вида, то правило можно применить снова, переходя ко вторым производным и т.д.
Пример. Вычислить  .
.
Решение. Функции  и
и  бесконечно большие при
бесконечно большие при 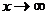 , т.е. имеем неопределенность вида
, т.е. имеем неопределенность вида  . Применяем правило Лопиталя:
. Применяем правило Лопиталя:
 =
=  . Снова при
. Снова при 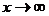 имеем неопределенное выражение
имеем неопределенное выражение  . Повторное применение правило Лопиталя приводит к следующему результату:
. Повторное применение правило Лопиталя приводит к следующему результату: 

|
|
|
Задачи для контрольной работы
1.3.2.Вычислить пределы:
1.  10.
10.  18.
18. 
2.  11.
11.  19.
19. 
3.  12.
12.  20.
20. 
4.  13.
13.  21.
21. 
5.  . 14.
. 14.  22.
22. 
6.  15.
15.  23.
23. 
7.  16.
16.  24.
24. 
8.  17.
17.  25.
25. 
9. 
Применение производной к исследованию функций
Исследование по первой производной: монотонность, экстремумы
В основе исследования функции на монотонность (возрастание, убывание) и экстремумы (максимумы, минимумы) лежат следующие положения:
а) интервалы, где, служат интервалами возрастания функции 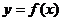 ; на интервалах, где
; на интервалах, где  , функция убывает;
, функция убывает;
б) точки перемены знака  с «+» на «-» служат точками максимума (точка наибольшего значения функции среди всех ее значений из некоторой окрестности этой точки) , а с «-» на «+» - точками минимума (точка наименьшего значения функции в некоторой окрестности).
с «+» на «-» служат точками максимума (точка наибольшего значения функции среди всех ее значений из некоторой окрестности этой точки) , а с «-» на «+» - точками минимума (точка наименьшего значения функции в некоторой окрестности).
|
|
|
1.4.2. Исследование по второй производной: характер выпуклости
Говорят, что дуга линии имеет определенный характер выпуклости, если она пересекается с любой своей секущей не более, чем в двух точках. Такая дуга лежит по одну сторону от касательной, проведенной в любой точке дуги: если целиком ниже касательной, то дуга называется выпуклой (выпуклой вверх), а если выше – то вогнутой (выпуклой вниз).
В основе исследования функции на характер выпуклости лежат следующие положения:
а) интервалы, где  , служат интервалами вогнутости графика функции
, служат интервалами вогнутости графика функции 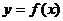 ; на интервалах, где
; на интервалах, где  , график функции выпукл;
, график функции выпукл;
б) точки перемены знака второй производной  служат точками перегиба графика, т.е. точками перемены характера выпуклости.
служат точками перегиба графика, т.е. точками перемены характера выпуклости.
Асимптоты графика
Вертикальная асимптота 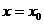 графика функции
графика функции 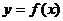 возникает во всякой точке
возникает во всякой точке  , где эта функция не определена, и хотя бы один из односторонних ее пределов в точке
, где эта функция не определена, и хотя бы один из односторонних ее пределов в точке  равен бесконечности.
равен бесконечности.
График функции обладает асимптотой  на бесконечности (наклонной асимптотой), если существуют оба числа (оба предела)
на бесконечности (наклонной асимптотой), если существуют оба числа (оба предела)
 ;
;
при этом, вообще говоря, следует рассмотреть отдельно оба случая  и
и  .
.
|
|
|
Если первый из указанных пределов не существует, или существует первый, но не существует второй, то график не обладает асимптотой (на бесконечности соответствующего знака).
1.4.4. Алгоритм полного исследования функции
1. Исследование элементарными методами: область определения, характер четности, периодичность.
2. Точки разрыва, вертикальные асимптоты.
3. Исследование на монотонность и экстремумы.
4. Характер выпуклости, точки перегиба.
5. Асимптоты на бесконечности.
Пример. Исследовать функцию  и построить ее график.
и построить ее график.
Решение.
1. Функция определена при всех  . Поскольку ее область определения не обладает симметрией относительно начала координат, то вопрос о характере четности не стоит: функция ни четна, ни нечетна. Очевидно, что функция непериодична.
. Поскольку ее область определения не обладает симметрией относительно начала координат, то вопрос о характере четности не стоит: функция ни четна, ни нечетна. Очевидно, что функция непериодична.
2. Функция претерпевает разрыв при  Исследуем ее поведение при стремлении х к 1 слева (т.е. при
Исследуем ее поведение при стремлении х к 1 слева (т.е. при  , что обозначается в виде
, что обозначается в виде  и справа (т.е. при
и справа (т.е. при  , что обозначается в виде
, что обозначается в виде  . В первом случае функция остается отрицательной, и знаменатель дроби стремится к нулю, так что
. В первом случае функция остается отрицательной, и знаменатель дроби стремится к нулю, так что
 .
.
Во втором случае дробь будет положительной, поэтому
 .
.
Следовательно, прямая х=1 служит вертикальной асимптотой графика.
3. Имеем  Критическими точками первой производной (т.е. точками, где она не определена или обращается в ноль), служат точки
Критическими точками первой производной (т.е. точками, где она не определена или обращается в ноль), служат точки  Этими точками числовая ось разбивается на интервалы знакопостоянства производной
Этими точками числовая ось разбивается на интервалы знакопостоянства производной  При
При  имеем
имеем  , а значит функция возрастает; при
, а значит функция возрастает; при  а также при
а также при  имеем
имеем  , так что в каждом из этих интервалов функция убывает; наконец,
, так что в каждом из этих интервалов функция убывает; наконец,  при
при  , так что в этом интервале функция возрастает.
, так что в этом интервале функция возрастает.
В точке х=0 производная  изменила свой знак с «+» на «-», следовательно, в этой точке данная функция достигла своего максимального значения:
изменила свой знак с «+» на «-», следовательно, в этой точке данная функция достигла своего максимального значения:  .
.
В точке х=2 производная  изменила свой знак с «-» на «+», так что в этой точке данная функция приняла минимальное значение:
изменила свой знак с «-» на «+», так что в этой точке данная функция приняла минимальное значение: 
- Найдем вторую производную:

Имеем  при
при  , так что в указанном интервале график функции выпукл;
, так что в указанном интервале график функции выпукл;  при
при  , следовательно, в интервале
, следовательно, в интервале  график вогнут. В точке х=1 (критическая точка второй производной) функция не определена; следовательно, точек перегиба график не имеет.
график вогнут. В точке х=1 (критическая точка второй производной) функция не определена; следовательно, точек перегиба график не имеет.
5. Определяем асимптоты графика на бесконечности (наклонные асимптоты). В случае  коэффициенты уравнения прямой
коэффициенты уравнения прямой  будут следующими (если соответствующие пределы будут существовать):
будут следующими (если соответствующие пределы будут существовать):

Итак,  , так что график обладает асимптотой
, так что график обладает асимптотой  на
на  Точно такие же вычисления пределов при
Точно такие же вычисления пределов при  приводят к следующему результату: график обладает той же асимптотой
приводят к следующему результату: график обладает той же асимптотой  и на
и на 
Соединяя результаты полного исследования, изображаем эскиз графика функции:

Дата добавления: 2018-02-15; просмотров: 477; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
