Задачи для контрольной работы. Рекомендовано редакционно-издательским советом университета
УДК
ББК
Рекомендовано редакционно-издательским советом университета
Рецензент
Кандидат технических наук доцент ГОУ ВПО ТГТУ
Е.Е. Мордовина
| Нахман А. Д., Петрова Е.А. | |
| «Дифференциальное исчисление функций одной и нескольких переменных»: Методические указания и контрольные задания. Тамбов: Изд-во ГОУВПО ТГТУ, 2012. - 32 с. ISBN | |
| Приведены краткие теоретические сведения и алгоритмы решения стандартных задач по разделу курса математики "Дифференциальное исчисление функций одной и нескольких переменных". Предложены 25 вариантов контрольных заданий. Для студентов очной и заочной форм обучения. |
Введение
Настоящие методические разработки подготовлены в соответствии с требованиями ФГОС ВПО к основным образовательным программам естественно-математической подготовки бакалавров. Издание адресовано студентам 1 курса инженерных направлений. Целью издания является формирование и закрепление навыков в области решения задач по дифференциальному исчислению функций одной и нескольких переменных. В силу ограниченного объема работы авторы избегали точных формулировок основных определений и теорем, ограничиваясь объяснением смысла понятий и утверждений. По этой причине, студенту предварительно следует ознакомиться с соответствующим теоретическим материалом по учебнику или конспекту лекций.
|
|
|
Работа построена по модульному принципу. Речь идет о следующих модулях содержания:
предел и производная функции одной переменной, приложения производной (в том числе, к исследованию функций), частные производные функций нескольких переменных, приложения дифференциального исчисления функций нескольких переменных (в том числе, в теории скалярного поля и к исследованию экстремального поведения функций).
Образцы решений типовых задач предваряются изложением соответствующего алгоритма. Каждый параграф заканчивается перечнем контрольных заданий. Задачи составлены так, чтобы в процессе их решения не возникали технические трудности, преодоление которых «затушевывает» суть дела. Преподаватель, по своему усмотрению, может варьировать объем и уровень трудности заданий. Так, например, в заданиях на исследование функции минимальные требования могут быть сведены лишь к применению первой производной (исследование характера монотонности и экстремумов функции). Банк предлагаемых здесь задач может быть использован для формирования контрольных работ, адресованных студентам как очной, так и заочной форм обучения.
Дифференциальное исчисление функций одной переменной
|
|
|
Предел функции одной переменной
1.1.1. Понятие предела – одно из основных в математическом анализе. Не приводя строгих определений, объясним смысл указанного понятия. Пусть дана функция 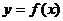 и значения аргумента х неограниченно приближаются к значению
и значения аргумента х неограниченно приближаются к значению  , но не совпадают с
, но не совпадают с  (что будем записывать в виде
(что будем записывать в виде  ). Если при этом оказывается, что значения
). Если при этом оказывается, что значения 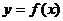 становятся сколь угодно близкими к некоторому числу А, то говорят, А есть предел функции
становятся сколь угодно близкими к некоторому числу А, то говорят, А есть предел функции  в точке
в точке  и записывают
и записывают 
 .
.
В случае, когда значения аргумента х неограниченно растут по модулю, оставаясь при этом положительными (отрицательными), мы записываем  (
(  ). Если не принципиально, какого знака значения аргумента х, то употребляем символ
). Если не принципиально, какого знака значения аргумента х, то употребляем символ  Запись
Запись  означает, что значения
означает, что значения 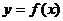 становятся сколь угодно близкими к числу А при
становятся сколь угодно близкими к числу А при  Говорят также, что число А есть предел функции на бесконечности.
Говорят также, что число А есть предел функции на бесконечности.
Если в (любом из трех рассмотренных случаев) А=0, то функция 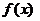 называется бесконечно малой.
называется бесконечно малой.
Возможен также случай, когда значения функции 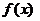 неограниченно растут (к
неограниченно растут (к  или -
или -  ) при стремлении аргумента х к некоторому
) при стремлении аргумента х к некоторому  или к бесконечности. В этих случаях записывают соответственно
или к бесконечности. В этих случаях записывают соответственно
 и
и 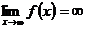 ,
,
а функцию 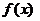 называют бесконечно большой (при
называют бесконечно большой (при  и
и  соответственно).
соответственно).
|
|
|
Следует заметить, что если функция 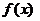 - бесконечно большая (бесконечно малая), то функция
- бесконечно большая (бесконечно малая), то функция  бесконечно малая (бесконечно большая).
бесконечно малая (бесконечно большая).
Если рассмотреть, в частности, функцию натурального аргумента (последовательность) 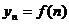 , то к ней применимо определение предела на бесконечности; используют запись
, то к ней применимо определение предела на бесконечности; используют запись
 .
.
1.1.2. Всякая элементарная функция  непрерывна на своей области определения
непрерывна на своей области определения  . Это означает возможность перехода к пределу под знаком функции
. Это означает возможность перехода к пределу под знаком функции  во всякой точке
во всякой точке  :
:  .
.
Этим свойством пользуются при вычислении пределов. Кроме того, при выполнении арифметических операций над функциями соответствующие операции выполняются и над их пределами.
1.1.3. Неопределенностями (при  или
или  ) называются такие выражения (под знаком предела), которые при формальной подстановке вместо аргумента х предельного значения (
) называются такие выражения (под знаком предела), которые при формальной подстановке вместо аргумента х предельного значения (  или
или  ) принимают вид
) принимают вид  ,
,  и др.
и др.
1.1.4. Приемы вычисления пределов. Вычисление пределов рациональных или иррациональных дробей на бесконечности может быть произведено путем одновременного деления числителя и знаменателя на старшую степень аргумента, чем достигается переход от бесконечно больших к бесконечно малым. Продемонстрируем прием на следующем примере.
|
|
|
Пример. Вычислить  .
.
Решение. Имеем бесконечно большие в числителе и знаменателе дроби; следовательно, выполняем одновременное деление на старшую степень аргумента, т.е. на 
 =
= 
Теперь имеем бесконечно малую в знаменателе дробь и функцию, стремящуюся к  в числителе, т.е. дробь оказывается бесконечно большой. Ответ записываем в виде
в числителе, т.е. дробь оказывается бесконечно большой. Ответ записываем в виде
 .
.
Пример. Вычислить  .
.
Решение. Имеем неопределенность вида  . Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, т.е. на
. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, т.е. на  и сократим числитель и знаменатель на общий множитель х , (который при
и сократим числитель и знаменатель на общий множитель х , (который при  не равен нулю). В результате имеем
не равен нулю). В результате имеем

так что искомый предел равен 0,5.
1.1.5. Замечательные пределы.
1) При 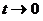 отношение
отношение  представляет собою неопределенность вида
представляет собою неопределенность вида  . Можно доказать, что
. Можно доказать, что 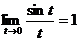 .
.
2) При 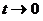 показательно-степенное выражение вида
показательно-степенное выражение вида 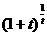 представляет собою неопределенность вида
представляет собою неопределенность вида 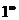 . Можно доказать, что соответствующий предел существует и равен некоторому иррациональному числу е=2,7…:
. Можно доказать, что соответствующий предел существует и равен некоторому иррациональному числу е=2,7…:  .
.
Рассмотренные пределы называются , соответственно, первым и вторым замечательными пределами. Второй замечательный предел может быть также записан в равносильной форме
 .
.
Пример. Вычислить a)  , б)
, б)  , в)
, в)  .
.
Решение. а) Имеем неопределенность вида  . Заметим, что при
. Заметим, что при 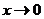 (см. первый замечательный предел) отношение
(см. первый замечательный предел) отношение  (вместе с
(вместе с  ) стремится к единице. При вычислении предела отношения
) стремится к единице. При вычислении предела отношения  можно снова воспользоваться первым замечательным пределом, если положить
можно снова воспользоваться первым замечательным пределом, если положить 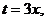 и заметить, что
и заметить, что  при
при 
 . Остается выполнить преобразование
. Остается выполнить преобразование
 =
= 
и закончить вычисление:
 =3
=3 

б) Имеем «комбинированную» неопределенность вида  . Если выделить в скобках в качестве слагаемого число 1, то станет возможным использование второго замечательного предела:
. Если выделить в скобках в качестве слагаемого число 1, то станет возможным использование второго замечательного предела:
 =
=  .
.
Теперь  при
при 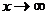 , поэтому в показателе степени удобно выделить выражение вида
, поэтому в показателе степени удобно выделить выражение вида 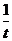 , т.е.
, т.е. 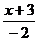 :
:
 =
=  .
.
Теперь, пользуясь свойством непрерывности показательно-степенной функции, перейдем по-отдельности к пределу в основании и показателе степени:
 (второй замечательный предел при
(второй замечательный предел при 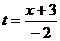 ),
), 
Имеем  .
.
в) Непосредственная подстановка значения 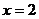 приводит к неопределенному выражению вида
приводит к неопределенному выражению вида  . Снова используем прием выделения слагаемого, равного 1:
. Снова используем прием выделения слагаемого, равного 1:
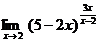 =
= 
Задачи для контрольной работы
Вычислить пределы:
1. а)  б)
б) 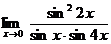 в)
в) 
2. а)  б)
б) 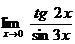 в)
в) 
3. а)  б)
б)  в)
в) 
4. а)  б)
б)  в)
в) 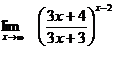
5. а)  б)
б)  в)
в) 
6. а)  б)
б)  в)
в) 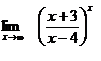
7. а)  б)
б)  в)
в) 
8. а)  б)
б)  в)
в) 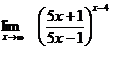
9. а)  б)
б)  в)
в) 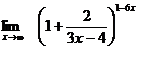
10. а)  б)
б)  в)
в) 
11. а) 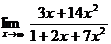 б)
б)  в)
в) 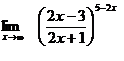
12. а)  б)
б)  в)
в) 
13. а)  б)
б)  в)
в) 
14. а)  б)
б)  в)
в) 
15. а)  б)
б) 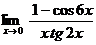 в)
в) 
16. а) 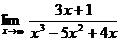 б)
б) 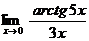 в)
в) 
17. а)  б)
б)  в)
в) 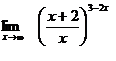
18. а)  б)
б)  в)
в) 
19. а)  б)
б)  в)
в) 
20. а) 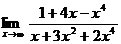 б)
б)  в)
в) 
21. а)  б)
б)  в)
в) 
22. а) 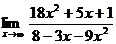 б)
б)  в)
в) 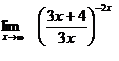
23. а) 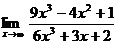 б)
б)  в)
в) 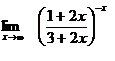
24. а)  б)
б)  в)
в) 
25. а)  б)
б)  в)
в) 
1.2. Производная функции одной переменной
1.2.1. Если значение аргумента  функции
функции  получило приращение
получило приращение  (изменилось на величину
(изменилось на величину  ), то соответствующее приращение (изменение) функции
), то соответствующее приращение (изменение) функции  есть
есть  . Величину
. Величину  естественно назвать средней скоростью изменения функции
естественно назвать средней скоростью изменения функции  , соответствующей изменению аргумента от х до х+
, соответствующей изменению аргумента от х до х+  ; «мнговенной» же скоростью изменения функции в точке х тогда следует считать предел вида
; «мнговенной» же скоростью изменения функции в точке х тогда следует считать предел вида


называемый производной функции f и обозначаемый  ,
,  или
или  . Операция взятия производной называется дифференцированием функции.
. Операция взятия производной называется дифференцированием функции.
1.2.2. Таблица производных основных элементарных функций.
1)  ; 9)
; 9)  ;
;
2)  ; 10)
; 10)  ;
;
3)  ; 11)
; 11)  ;
;
4)  ; 12)
; 12) 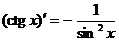 ;
;
5)  ; 13)
; 13)  ;
;
6)  ; 14)
; 14)  ;
;
7)  ; 15)
; 15)  ;
;
8)  ; 16)
; 16)  .
.
1.2.3. Правила дифференцирования. Пусть  ,
,  ,
,  , тогда
, тогда
1. 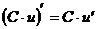 ;
;
2.  ;
;
3.  ;
;
4.  .
.
1.2.4. Производная сложной функции  вычисляется по правилу
вычисляется по правилу
 , где
, где  Так, например,
Так, например,

1.2.5. Если зависимость  задана параметрически, т.е. в виде
задана параметрически, т.е. в виде  , то производная
, то производная  (или, в других обозначениях,
(или, в других обозначениях, 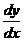 ) вычисляется по формуле
) вычисляется по формуле

1.2.6.Производная  также может рассматриваться как некоторая функция; в этом случае можно говорить о ее производной как второй производной данной функции:
также может рассматриваться как некоторая функция; в этом случае можно говорить о ее производной как второй производной данной функции:  . Аналогично можно рассматривать третью и другие производные (производные высших порядков).
. Аналогично можно рассматривать третью и другие производные (производные высших порядков).
Примеры. 1. Вычислить  , если
, если  .
.
Решение. В силу правил дифференцирования  . Здесь мы имеем сложную логарифмическую функцию, а именно функцию аргумента
. Здесь мы имеем сложную логарифмическую функцию, а именно функцию аргумента  . По формуле дифференцирования натурального логарифма «сложного аргумента» получаем тогда
. По формуле дифференцирования натурального логарифма «сложного аргумента» получаем тогда 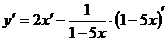 =
=  .
.
2. Материальная точка движется прямолинейно, при этом зависимость пройденного расстояния  от времени
от времени  (закон движения) имеет вид
(закон движения) имеет вид  . Найти скорость
. Найти скорость  точки в момент
точки в момент  .
.
Решение. Согласно п.1.2.1 достаточно вычислить производную в точке  . По формуле дифференцирования произведения и с учетом правила дифференцирования сложной функции мы имеем
. По формуле дифференцирования произведения и с учетом правила дифференцирования сложной функции мы имеем


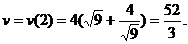
3. Найти производную функции, заданной параметрически:  .
.
Решение. Имеем: 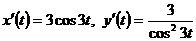 , а тогда по формуле дифференцирования функции, заданной параметрически, получаем
, а тогда по формуле дифференцирования функции, заданной параметрически, получаем 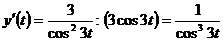 .
.
Дата добавления: 2018-02-15; просмотров: 402; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
