Теорема Ляпунова об асимптотической устойчивости.

Если можно найти функцию  такую, что она непрерывна и дифференцируема, в нуле она минимальна и =0, больше у нее нет экстремумов, производная этой функции по времени <0, кроме самого 0, то тогда положение равновесия асимптотически устойчиво.

 

Теорема Четаева о неустойчивости.

Если можно подобрать  такую, что:

1) непрерывна и дифференцируема

2) в любой сколь угодно малой окрестности начала координат существует область v>0

3)  везде в области v>0,

то положение равновесия неустойчивое.

 

Случай малого коэффициента при старшей производной.

1) – неустойчивое

2) и 3) – полуустойчивые (с точки зрения математики) и неустойчивые (с точки зрения физики)

4) – устойчивое

Дифференциальные уравнения в частных производных.

ДУ в частных производных называется уравнение, связывающее функцию нескольких переменных, сами эти переменные и частные производные функции по этим переменным.

Если все  не зависят от производных, то уравнение называется линейным или квазилинейным.

Если хотя бы одна  зависит от z, то уравнение квазилинейное.

Если в уравнении Z=0, то уравнение однородное.

 

Решение линейного однородного уравнения.

- уравнение характеристики

Решение этой системы называется характеристики.

Общим решением однородного линейного ДУ в частных производных будет некоторая произвольная функция от n-1 первого интеграла.

.

1)

2)

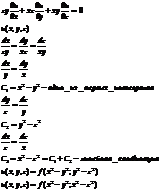
Неоднородные линейные и квазилинейные уравнения.

квазилинейное неоднородное

- ищем решение в неявном виде

- линейное однородное уравнение

- общее решение

- уравнение квазилинейное, но однородное

 

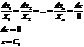
Решение задачи Коши.

- решение этого ДУ

не являются константами

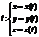
 выбираем так, чтобы через точку P проходила интегральная поверхность.

Для  делаем тоже самое.

Эти две плоскости пересекутся по линии проходящей через точку P.

Все эти линии образуют поверхность, которая тоже будет являться интегральной поверхностью (т.к. все прямые принадлежат интегральным поверхностям).

Геометрический способ.

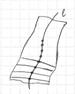
т.к. через каждую точку проходит одна характеристика, то и поверхность будет единственной.

l – не характеристика.

Если l – характеристика. Берем точку на l и проводим через нее характеристику, которая совпадет с l. И т.д. для всех точек на l.

Поверхность содержит в себе линию l и все семейство характеристик.

Т.к. таких поверхностей может быть много, то решений бесконечно много.

 

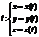
1) l – не характеристика

2) l – характеристика

---

Дата добавления: 2018-02-15; просмотров: 808; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!