Линейные однородные уравнения с постоянными коэффициентами.
Уравнения с постоянными коэффициентами всегда можно решить.
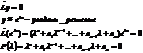
- характеристический многочлен.
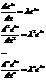
- характеристическое уравнение.
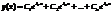
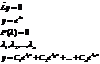
1) комплексные корни
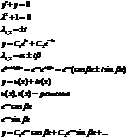
2) кратные корни
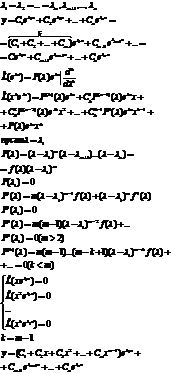
Линейные неоднородные уравнения.
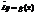
1) Теорема об общем решении.
Общее решение неоднородного уравнения складывается из общего решения соответствующего ему однородного уравнения и частного решения неоднородного уравнения.
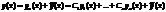Док-во:
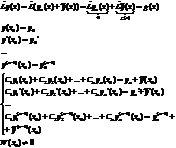2) Допустим есть S уравнений типа:
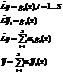
Док-во:
3) Если 
чисто действит.
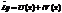, то тогда
Неоднородное линейное уравнение с постоянными коэффициентами и со специальной правой частью.
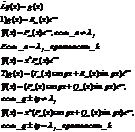
Метод Лагранжа вариации произвольных постоянных для уравнения 2-ого порядка.
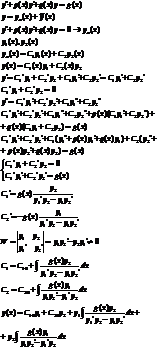
Уравнения Эйлера.
Однородные уравнения Эйлера.
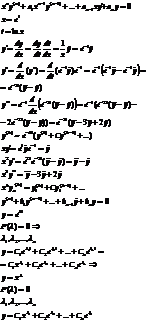
1) 2 комплексно сопряженных корня, остальные разные
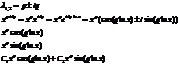2) корни действительные, но кратные
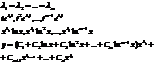3) корни кратные и комплексно сопряженные
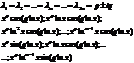
Неоднородные уравнения Эйлера.
Если и не специального вида, то используем метод Лагранжа.
Если правая часть специального вида:
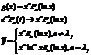
m – кратность корня.
Системы обыкновенных дифференциальных уравнений первого порядка.
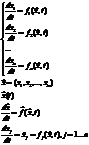
Теорема существования и единственности.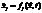 
Если все функции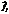 
непрерывны и непрерывны их частные производные 
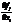в окрестности точки 
, тогда существует единственное решение этого уравнения, удовлетворяющее начальному условию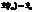 
|
|
|
Поле направлений.
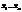-равноправные решения 
Пространство этих переменных – координаты фазового пространства.
- фазовая траектория
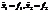
t – время.
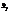- фазовые скорости.
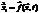
1. Неавтономные системы. Это та, для которой 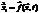, но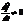 
В неавтономных системах фазовые траектории могут пересекаться.
2. Автономные системы. Это когда 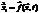, но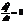 
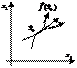
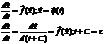
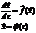
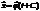-для автономных систем
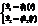-для пересекающихся решений
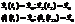
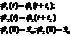
Два разных решения обладают одним и тем же начальным условием, а по теореме о существовании и единственности такого быть не может. Следовательно, решения автономных систем не пересекаются.
Сведение системы n уравнений 1-го порядка к одному уравнению порядка n.
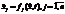
Первые n-1 уравнений рассмотрим как алгебраическую систему относительно 
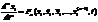
Системы линейных уравнений.
Линейные – это те уравнения, в которые функция и её производная входят линейным образом.
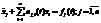
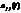- непрерывны
1. 
линейная однородная система.
1) Если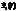 
- решение однородной системы, 
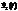- тоже её решение, тогда суперпозиция этих решений с постоянными коэффициентами тоже будет решением: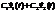 
2) Если решение имеет комплексный вид, тогда каждая из функций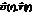 
по отдельности также будет решением при условии, что само уравнение было действительным.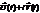 
|
|
|
3) Общее решение находится как сумма всех частных линейно независимых решений с постоянными коэффициентами.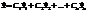 
2. 
- неоднородные системы
1) Если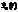 
- какое-то частное решение однородного уравнения, а 
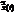- частное решение неоднородного уравнения, тогда 
тоже будет каким-то частным решением неоднородного уравнения.
2) Общее решение неоднородного уравнения складывается из общего решения однородного уравнения и любого частного решения неоднородного уравнения: 
3) Если правая часть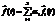 
является суперпозицией некоторых функций, а 
- частное решение системы с правой частью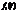 
, тогда частное решение, соответствующее правой части 
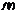, будет иметь вид: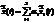 
Дата добавления: 2018-02-15; просмотров: 523; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!