Уравнения 1-ого порядка не разрешенные относительно производной.
1) уравнения которые не разрешены, но их можно разрешить относительно производной
2) уравнения, которые невозможно разрешить относительно производной
Теорема существования и единственности решения.
Если в некоторой области D на плоскости XY выполняются следующие условия:
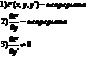
тогда через каждую точку области D проходит одна интегральная кривая по данному направлению.
Особой является точка, через которую не проходит ни одного решения или нескольких с одинаковыми касательными.
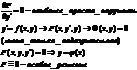
Метод введения параметра.
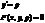
1) Уравнения разрешенные относительно y
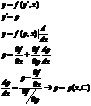
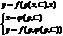
- общее решение в параметрическом виде.
2) Уравнения разрешенные относительно x.
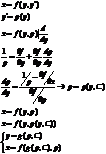
- общее решение в параметрическом виде.
Уравнения Лагранжа и Клеро.
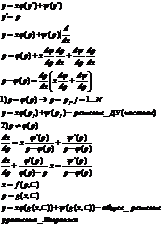
Уравнение Клеро.
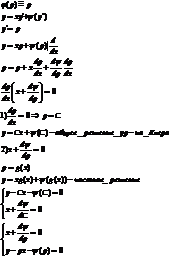
Дифференциальные уравнения высших порядков.
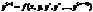
Теорема существования и единственности решения.
Если в некоторой области D на плоскости XY непрерывны и ограничены сама функция f, а так же ее частные производные по y,y’,y”,…,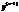 
, то тогда в этой области через любую точку будет проходить единственная интегральная кривая, удовлетворяющая следующим условиям:
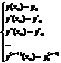-начальные условия
через любую точку будет проходить бесконечное число интегральных кривых.
Дифференциальные уравнения семейства кривых.
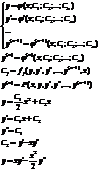
Методы понижения порядка ДУ.
1) Уравнения не содержащие саму ф-ию и ее производные до (m-1) порядка
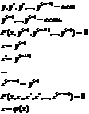
2) Уравнения не содержащие x
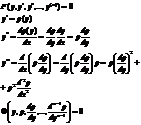
3) 
Линейные ДУ.
если g(x)=0 – линейное уравнение однородно
если 
- неоднородно.
Введем линейный дифференциальный оператор
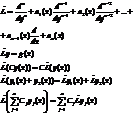
Линейные однородные уравнения.
1) Если функции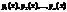 
являются решениями линейного ДУ, то 
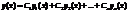тоже будет решением.
2) Теорема о комплексных решениях.
Решаем уравнение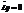 
и находим решения этого уравнения в комплексном виде:
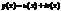. Тогда каждая из функций u(x) и v(x) в отдельности так же являются решениями этого ДУ.
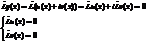
Функции 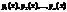называются линейно зависимыми, если 
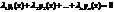при не всех 
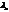равных 0.
Функции линейно независимы, если это равенство выполняется при всех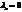 
.
Определить Вронского.
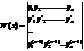
3) Если функции 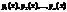являются линейно зависимыми, то определитель Вронского этой системы функций равен 0.
4) Если функции 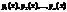являются линейно независимыми частными решениями ДУ 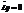, то определитель Вронского этой системы функций будет отличен от 0 при любых x.
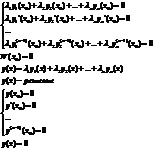
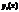- линейно зависимы, что противоречит условию.
Следовательно 
.
5) Общее решение однородного линейного ДУ порядка n записывается в виде линейной комбинации n любых линейно независимых частных решений этого ДУ.
Порядок и число решений должны совпадать.
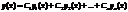
1) y(x) - решение
2) Докажем, что решение общее 
это решение общее.
Следствие: у линейного уравнения порядка n должно быть n линейно независимых частных решений.
Фундаментальная система решений данного уравнения – n линейно независимых решений ДУ порядка n.
6) Фундаментальная система решений ДУ всегда существует.
Дата добавления: 2018-02-15; просмотров: 864; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!