Огибающая как особое решение ДУ.
Дифференциальное уравнение – равенство, связывающее неизвестную функцию, ее аргумент и производную данной функции. Порядок ДУ – порядок старшей производной входящей в уравнение. Решение ДУ – такая функция, подстановка которой в ДУ приводит его к тождеству. Виды ДУ: 1) Обыкновенные ДУ: У., в которое входит функция и ее производная, которая зависит только от одной переменной (y(x)). 2) ДУ в частных производных: 1) ДУ первого порядка: Общее решение ДУ – функция , где C=const, если она удовлетворяет этому уравнению при любом значении константы C. Исходя из начальных условий, всегда можно найти соответствующее этому условию значение С. Частное решение ДУ – функция , в которой значение С положено равному какому-то конкретному числу. ДУ первого порядка разрешенные относительно производной y’=f(x,y).
Теорема существования и единственности решения.
Если в некоторой области D на плоскости XY функция f(x,y) непрерывна и ее частная производная 
непрерывна, то тогда через любую точку из области D с координатами 
проходит решение ДУ (интегральная кривая) причем, только одно.
Точки, в которых решение не единственное или его нет – особые точки.
Поле направлений и изоклины.
Кривые на плоскости XY, отображающие решение ДУ – интегральные кривые.
1) ДУ с разделенными переменными
2) ДУ с разделяющимися переменными
|
|
|
3) Однородные ДУ
4) 
5)
Линейные уравнения 1-ого порядка.
Если функция q(x)=0 – уравнение однородное.
Если q(x) не равно 0 – неоднородное.
Метод Лагранжа вариации произвольной постоянной.
Уравнение Бернулли.
Уравнения в полных дифференциалах.
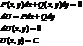
уравнение называется уравнением в полных дифференциалах если его левая часть является полным дифференциалом функции U.
Признак полного дифференциала:
Для того чтобы выражение Pdx+Qdy было полным дифференциалом функции U(x,y) необходимо и достаточно, чтобы 
.
1) необходимость
2) достаточность
Интегрирующий множитель.
Функция, при домножении на которую уравнение становится уравнением в полных дифференциалах – интегрирующий множитель.
Огибающие. Семейство интегральных кривых.
Огибающей называется линия, которая в каждой своей точке касается одной из кривых семейства, причем в разных точках она касается разных кривых.
Рассмотрим не огибающую, а интегральную кривую.
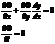
Изогональные и ортогональные траектории.
Линия, которая пересекает все интегральные кривые под одним и тем же углом, называется изогональной траекторией. Если угол составляет 90 градусов, то такая траектория называется ортогональной.
|
|
|
y(x) – изогональная траектория
- уравнение изогональной траектории.
- уравнение ортогональной траектории.
Особые точки.
особая точка – точка, через которую не проходит ни одного решения или проходит более 1.
1)
- особые точки (узел)
y=0 x=0 – тоже решение
точка x=0 – особая точка (ядро)
2)
x=0 –особая точка (ядро)
x=0 -особая точка (центр)
3)
x=0 – особая точка (фокус)
Особые решения.
особенность – более одного решения
- особая линия +решение
эта линия с одной стороны является особой кривой, с другой стороны она является интегральной линией, такие линии называются особыми решениями.
y=0 – тоже решение ДУ, через каждую ее точку проходит более 1 кривой – значит она особое решение.
Особое решение не может быть получено из общего интеграла ДУ 
.
Огибающая как особое решение ДУ.
Докажем что решение.
В каждой точке огибающая касается какой-то интегральной кривой.
Если огибающая касается интегральной кривой, то касательные одинаковы у интегральной кривой и огибающей
Огибающая – решение.
Докажем, что это особое решение. Через каждую точку огибающей как минимум 2 решения, это интегральная линия и саама огибающая 
огибающая – особое решение ДУ.
|
|
|
Замечание:
Допустим, что есть линия 
, которая является особой.
не существует, значит, что эта линия особая, но не является решением.
Через каждую точку проходит более одной интегральной кривой.
Из этой системы находится линия, являющаяся алгебраическим местом особых точек, которая не является решением.
Вывод: из системы можно найти либо огибающую, либо особую кривую.
Дата добавления: 2018-02-15; просмотров: 1387; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!