Система уравнений с постоянными коэффициентами.
1. Однородные уравнения.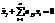 
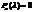- характеристическое уравнение
1. 
Подставим 
в систему. Получаем n неизвестных в n-1 уравнениях. Выразим
2. 
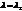
n.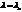 
Случай комплексных корней 
Нужно сгруппировать слагаемые при линейно независимых действительных функциях и переобозначить коэффициенты перед этими функциями.
Случай кратных корней 
Первые интегралы систем дифференциальных уравнений
- это первый интеграл данного дифференциального уравнения.
эти функции называются первыми интегралами нашей системы уравнений
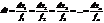
- симметричная форма записи нашей системы
Теория устойчивости.
- решение этого уравнения.
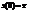- начальное условие
Опр Решение называется устойчивым по Ляпунову, если для любого сколь угодно малого 
найдётся 
такое, что для любого другого решения этого уравнения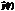 
, удовлетворяющего при 
условию 
, при 
выполняется условие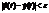 
.
Если при 
, то тогда решение называется асимптотически устойчивым.
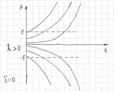
- неустойчиво.
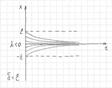
- устойчиво.
Положение равновесия (стационарная точка).
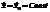- положение равновесия.
Если 
, то 
- стационарная точка.
Исследование на устойчивость произвольного решения всегда можно свести к исследованию на устойчивость положения равновесия.
Находим , которые хотим исследовать на устойчивость.
Введём 
Если - решение, то 
- стационарная точка.
|
|
|
Т.о. мы свели задачу об исследовании на устойчивость произвольного решения к исследованию на устойчивость положения равновесия.
Опр Положение равновесия называется устойчивым, если для любого сколь угодно малого найдётся такое, что для любого решения 
, удовлетворяющего при 
условию 
, при выполняется условие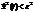 
.
Если при 
, то положение равновесия называется асимптотическим.
Метод Ляпунова. Исследование на устойчивость по линейному приближению.
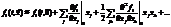
В случае, когда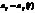 
(эти коэффициенты являются функциями времени) в общем случае мы эту задачу не решим.
Если реальные части всех показателей 
отрицательны, то положение равновесия является асимптотически устойчивым.
Если хотя бы один показатель имеет положительную реальную часть, то положение равновесия является неустойчивым.
Если хотя бы один показатель имеет нулевую реальную часть, притом, что все остальные показатели имеют отрицательную реальную часть, то ответить на вопрос об устойчивости нельзя. Отброшенные нелинейные слагаемые в этом случае могут сыграть главную роль, нужно дополнительное исследование.
Теорема Гурвица.
- матрица Гурвица
Для того чтобы положение равновесия было устойчивым необходимо и достаточно, чтобы все главные миноры матрицы Гурвица были больше 0.
|
|
|
Метод Ляпунова.
Теорема Ляпунова об устойчивости.
Если можно найти функцию 
такую, что она непрерывна и дифференцируема, в нуле она минимальна и =0, больше у нее нет экстремумов, производная этой функции по времени 
, то тогда положение равновесия устойчиво.
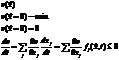
Дата добавления: 2018-02-15; просмотров: 502; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!