Показник ефективності структур
1. Оперативність – оцінюється часом реакції систем на вплив зовнішнього середовища або швидкістю зміни залежності від загальної схеми з’єднання елементів та їх застосування.
2. Централізація – визначає можливість виконання одним елементом системи керівних функцій. Чисельна централізація визначається середнім числом зв’язку центрального елемента з іншими.
3. Периферійність – характеризує просторові властивості структури. Чисельно периферійність характеризується показником *центра ваги структури*,при якому в якості одиничної оцінки міри зв’язності виступає *відносна вага* елемента структури.
4. Живучість – визначає здатність системи зберігати основні властивості при пошкодженні її частини. Цей показник може може характеризуватися відносним числом елементів, при пошкодженні яких показники ситеми не виходять за допустимі межі.
5. Об’єм – це кількісна характеристика структури. Визначається загальною кількістю елементів зв’язків. Об’єм пов’язаний з вартістю і другими характеристиками системи.
З кібернетичної точки зору об’єкт системи є лише перетворювач інформації вхідної у вихідну.
Стан системи в певний момент часу – це множина суттєвих можливостей у певний момент часу.
Процес – послідовна зміна зміна станів.
Статична система – система, стан якої практично не змінюється впродовж певного інтервалу часу.
Динамічна система – та, що змінює свій стан в часі.
Функція – зовнішній прояв властивостей об’єкта.
Емерджентність – це виникнення в системі нових інтегративних якостей, що не властиві її компонентам.
Неможливо передбачити властивості системи в цілому розбираючи і аналізуючи її по частинах.
Синергізм – це виявлення мультиплікативного ефекту при однонарпавлених діях.
Приклад:
З окремих деталей можна скласти світлофор, але якщо один з заборонених , то світлофор не буде працювати.
Роль математики в ТС
Матиматичне зображене моделювання
Життєвий цикл системи:
Проектування - виробництво – тестування – маркетинг – використання тех. обслуговування -утилізація.

Тривалість життєвого циклу більшості систем = 12 років.
Логістична крива


Класифікація рівнів складності:
1 рівень: мережа систем
2 рівень: система
3 рівень: передбачає оборонну мережу радарних систем
4 рівень: елементи
Система керування підсистем передавачів та виконавчих пристроїв, що виконують накази керування.
Підходи:
1.розбиття систем на певні елементи
Розбиття може бути процесом паралельним.
система – розбиття на підсистеми
2.Фізичне
3.Функціональне.

Модульні системи

Для управління складністю потрібно виділити кілька модулів та інтерфераційної взаємодії між ними.
1. Генетика
2. Виробництво прикладів зі змінними властивостями
3. Програмні бібліотеки стандартних модулів.
4. Комбінаторна лінія.
5. Проектування механічних або космічних систем
6. Проектування радіотехнічних систем
7. ЕЛ та ТК
8. Будівництво
Основною метою модуляційного підходу є
1. Керування складністю
2. Паралельна робота над модулями систем в той самий час
3. Підстановка систем до зовнішньої невизначеності
4. Різноманіття результуючих модульних систем
5. Гнучкість, адаптивність, здатність до змін конструкцій результуючих модульних систем
Висновки по модульності:
1. Модульність дозволяє простити процес проектування фази життєвого циклу
2. Якщо короткий ЖЦ, але довгий ЖЦ модулів.
3. Здатність до зміни конфігурації систем.
4. Спрощені проектування і підтримка систем продукції.
5. Спрощені проектування: Підтримка різних продукцій на основі бібліотек модулів, а також їх повторного використання.
Лекція 4
Структурне моделювання
Воно відбувається з використанням наступних основних методів:
1. Теорія графів
2. Теорія мереж
3. Теорія автоматів
Теорія графів передбачає використання власних графів передбачає використання власних графів, орт графів (напрямленого графа або орієнтивного графа) графів або орт графів з вагами ( для вершин, для ребер або дуг), прості графіки, ланцюги, дерева,паралельно – послідовні графіки, ієрархії.
Знакові графіки.
| a |
| b |
| c |
Граф: G = (A,E) де множина вузлів (вершин) A={1,…,n} і множина ребер E Í A×A (пари вершин)
Приклад: A={a, b, c}, E={(a, b), (b, c), (a, c)}
| a b c a 0 1 1 b 1 0 1 c 1 1 0 |
Матриця
Зображений на рисунку оргграф називається однонапрямленим оргграфом. Якщо дві стрілки будуть в різні сторони то отримаємо двонапрямлений орграф.
Граф у якому на ребрах вказують ваги, тобто число значення називається граф з вагою ребер.
Граф (вага ребер & вершин): G = (A,E) де множина ребер (вузлів) A={1,…,n} і множина ребер EÍ A×A (пари вершин) . Приклад: A={a, b, c}, E={(a, b), (b, c), (a, c)}
(вага вершин вказані в скобках)
Оргграф – передбачає використання множини вузлів (вершин) і множини дуг. Дуги є напрямлені і можуть бути у ній самій вершин.
Ієрархічні графи зображають деревоподібною системою, і якщо рівні ієрархії мають додаткові зв’язки.
Структури , що зображають графом:
 ланцюг
ланцюг
| a(1) |
| b(2) |
| c(4) |
дерево
Паралельно-послідовні рамки

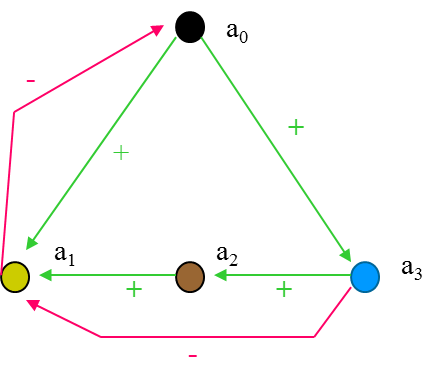

Графи згладжених дуг є у вигляді векторів
Метод – це міра близькості між вершиною.
Група оптимізації на графа
1. Найкоротший шлях, алгоритм Бальмена, алгоритм Дікстр
2. Задачі про комівояжера
3. Задача про мандрівника
Квастиризація – це розбиття на групи взаємопов’язаних або близьких елементів.
Оптимізація на графах

БАЗОВИЙ ГРАФ (ОРГРАФ):
Вага для дуг (ребер)
 Найкоротший шлях < a0,a9 >:
Найкоротший шлях < a0,a9 >:
L = < a0,a1,a2,a3,a4,a7,a9 >
2+1+1+2+2 = 8
Дерево покриття

Бінарне відношення R – це підмножина.
1. Домінування
2. Еквівалентність
Лекція 5
Дата добавления: 2018-02-15; просмотров: 541; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
