Вариация признаков, способы ее изучения, критерии оценки
Исчисляются в относительных величинах. Они позволяют сравнивать характер рассевания в различных распределениях. они рассчитываются на основании 1)-3) показателей
а) относительный показатель размаха вариации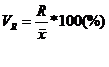 
б) относительный показатель среднего линейного отклонения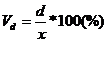 
в) относительный показатель СКО, этот показатель называют коэффициент вариации.
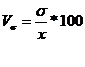
На основании этой группы показателей проводится оценка однородности совокупности, т.к. в ней устраняется несопоставимость, связанная с различными единицами измерения, а также несопоставимость, возникающая вследствие различия величин средних арифметических.
Для оценки однородности совокупности используют следующие критерии оценки.
Если коэф.вариации колеблется 0-10% – вариация слабая, ею можно пренебречь;
10-25% - вариация умеренная, совокупность считается однородной;
25-33% - вариация сильная, совокупность условно однородная;
более 33% - вариация очень сильная, совокупность неоднородна, материалы группировки следует перегруппировать.
Виды дисперсии. Правило сложения дисперсий
; 
; 
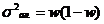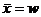
Правила сложения дисперсий.
Вариация ряда распределения в различных случаях принимает соответствующее разное соц.и экономическое значение.
Вариация индивидуальных значений определяется множеством факторов. Если рассматривать вариацию на основе сгруппированных данных, то фактор, положенный в основу группировки представляется систематическим фактором, но на величину результата оказывают влияние и другие факторы, неучтенные группировкой, т.е.случайные причины.
|
|
|
Силу влияния систематических и случайных причин можно выявить с помощью различных видов дисперсий. Такой анализ называется дисперсионным.
Виды дисперсий:
1.общая дисперсия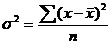 
, улавливает влияние всех факторов (систематических и случайных).
2.межгрупповая дисперсия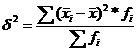 
, 
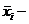среднее значение по каждой группе;
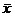- общая средняя в целом по совокупности, 
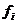- частота изучаемого признака по группам.
Улавливает влияние систематического фактора (положенного в основу группировки).
3.средняя внутригрупповая дисперсия (случайные причины):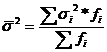
,
4.частная дисперсия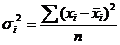 
, рассчитывается отдельно по каждой группе как средняя арифметическая простая. Необходима для расчета (3).
Правило сложения дисперсий: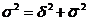 
.
Следствие из правила сложения дисперсий: если признак, положенный в основу группировки, значительно влияет на формирование изучаемого явления, то межгрупповая дисперсия будет близка к общей, и наоборот. Это означает, что группировочный признак не влияет на результат, если межгрупповая дисперсия далека от общей.
|
|
|
На основе полученных показателей дисперсией можно оценить силу тесноты связей. Это эмпирический показатель – эмпирическое корреляционное отношение 
- эта, изменяется от (-1) до1.
Знак показателя характеризует направление связи и исследователь его устанавливается логическим путем. Прямо пропорциональная связь со знаком «+», обратно пропорциональная – «-».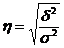 
Дата добавления: 2018-02-15; просмотров: 466; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!