Средние степенные величины. Принципы их применения
Средние степенные-обобщающая количественная характеристика, множество индивидуальных значений варьирующего признака в пределах одного явления и характеризует его типические черты в конкретных условиях пространства и времени. Но, несмотря на то, что средние – это реальные показатели и выражают объективно существующие свойства изучаемого явления, их нельзя использовать для характеристики процесса в целом.
При расчете показателей средних. Нужно учитывать их особенности и соблюдать след. требования:
1)осреднению подвергаются лишь количественные признаки; 2)количест.признаки должны варьировать;
3)средние рассчитываются для однородной совокупности; 4)осреднению подвергаются массовые данные;
5)нельзя увлекаться средними..
Средние степенные методически строятся по формуле средне степенной математически:
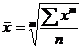(простая), где x- варианта, черта- знак осредениния, n- число слагаемых, m- степень возведения, от которой зависит вид средней , m=-∞;∞.
Применяют в условиях, когда исходная информация не сгруппирована – простая средняя, если сгруппирована – то средняя взвешенная: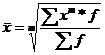 
, f- число повторений.
Средняя арифметическая, ее свойства
Из всех видов средних наибольшее распространение получило среднее арифметическое, которое обладает рядом математических свойств., которые используются в статистике:
1) 
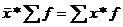
2)сумма отклонений индивидуальных значений от средней =0: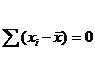 
|
|
|
3)Если каждую варианту разделить или умножить на постоянное число, то среднее арифметическое уменьшиться или увеличиться во столько же раз.
4)Если каждую варианту уменьшить или увеличить на какое-то постоянное число, то среднее арифметическое уменьшиться или увеличиться на это же число
5)Если все частоты разделить или умножить на какое-то постоянное число, то среднее арифметическое от этого не измениться.
Расчет средней по результатам группировки
Процедура выбора средней арифметической или гармонической:
1)если осредняется абсолютная величина или относительный показатель, прямо пропорциональный (данные не сгруппированы), то применяется средняя арифметическая простая;
2)Выбор вида средней по сгруппированным данным: выбор вида средней осуществляется логическим путем, если по логике расчета вес осредняемой величины располагается в знаменателе, то применяется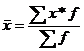 
; если же по логике расчета вес осредняемой величины располагается в числителе, то применяется гармон. взвешенная: 
.
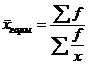Структурные средние, их использование в статистике
В зависимости от особенностей распределения ранжированных вариационных рядов, кроме средних, получили распространение структурные средние: мода, медиана, квартире, децили.
|
|
|
Структурные средние используются для анализа рядов распределения и для спец.аналитических целей.
Мода- величина признака, которая наиболее часто встречается в ряде распределения. Определяют по частоте.
Если ряд дискретный (значение группировочного признака) – то значение моды будет соответствовать наибольшей частоте.
Мода употребляется для характеристики некоторых типичных размеров общественных явлений. Которые не могут быть выражены средними показателями. Мода дает возможность определить преобладающий исследуемый уровень в данный момент. Возможно, что в распределении варианты встречаются одинаково часто, в этом случае говорят, что мода отсутствует, или в распределении встречается две варианты с наибольшей частотой – распределение бимодальное, если больше число раз – мультимодальное распределение. Бимодальное и мультимодальное распределение свидетельствуют о неоднородности совокупности.
В случае интервального ряда моду определяют по формуле Орджецкого:
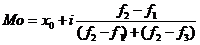, где x0- нижняя граница модального интервала; f1- частота предмодального интервала, f2- частота модального интервала, f3- частота после модального интервала, i- шаг интервала.
|
|
|
Медиана-значение признака у единицы, расположенной в середине упорядоченного ряда, и эта величина как бы делит упорядоченный ряд на две части, деление это производится по сумме накопленных частот:
№Me=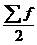 
-четный ряд; №Me= 
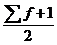- нечетный ряд.
Для интервального ряда Me рассчитывается по формуле Орджецкого:
Me=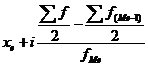 
, xe-нижняя граница медианного ряда, ∑f- накопленная частота вариационного ряда, ∑f(Me-1)- накопленная частота предмедианного интервала,
FMe- частота медианного интервала.
Свойства медианы: сумма отклонений членов ряда от медианы является величиной наименьшей (широко используется при планировании, при размещении тех или иных объектов…)
Если совокупность недостаточно однородна или ряд распределения имеет открытые интервалы, то возможно использование Me вместо средней арифметической величины.
Показатели моды и медианы часто используются для анализа рядов распределения, исходя из того, что при симметричном распределении членов ряда распределения, мода и медиана равны между собой. При асимметричном распределении медиана располагается в середине между средней и модой.
Дата добавления: 2018-02-15; просмотров: 1672; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!