Ряд распределения, его графическое изображение
Варианты - отдельные значения группировочного признака.
Частоты– числа, показывающие сколько раз встречает то или иное значение признака, если они выражены абсолютными величинами; если они выражены относительными величинами – то называются частости.
Ряды распределения могут быть построены по различным объектам: временные периоды, территориальные единицы.
Для наглядности распределения вариационные ряды изображают графически с помощью полигона (линейной диаграммы) (в основном дискретные ряды) и гистограммы (столбиковая диаграмма)(интервальные ряды).
Для их построения используется прямоугольная система координат, на оси абсцисс которой строится шкала значений вариантов (интервалов), а на оси ординат – частот (частостей). Основанием гистограммы служит величина интервалов значений хi, а высотой частота (частость). В случае неравенства интервалов в качестве высоты прямоугольников принимается плотность распределения – частное от деления частоты (частости) каждого интервала на его величину. Если основания полученных столбиков будет располагаться вертикально, а масштабная шкала наносится на горизонтальную ось, то получаем ленточные (полосовые) графики.
Выделяют также круговые диаграммы: площадь окружности принимается за величину всей изучаемой статистической совокупности, а площади отдельных секторов отображают удельный вес (долю) ее составных частей.
|
|
|
Радиальные диаграммы строятся на базе полярных координат, началом отсчета в них служит центр окружности, а носителем масштабных шкал являются радиусы круга. В основе их лежит повторяющиеся годовые циклы с помесячными и поквартальными данными, поэтому окружность делится на 12 равных частей. Каждому радиусу дается название месяца года и на каждом из них отмечается значение ряда, эти точки соединяются, и получается спиралеобразная линия.
Кумулята –строится по накопленным частотам (частостям), отражает их характер нарастания от группы к группе. Если оси поменять местами, то есть варианты откладывать на оси ординат, а накопленные частоты (частости) на оси абсцисс, то полученная кривая будет называтьсяогивой.
Статистические графики, правила оформления
Стат.график- чертеж, на котором при помощи условных геометрических фигур изображаются стат.данные.
Поле графика- это место, на котором он выполняется (лист бумаги, географическая карта, план местности и т.д.)
Графический образ- это символические знаки, с помощью которых изображаются стат.данные (линии, точки, плоски, иногда силуэты предметов).
Экспликация графика –это пояснение его содержания, включает в себя заголовок графика, объяснение масштабных шкал, пояснение отдельных элементов графического образа.
|
|
|
Требования к оформлению графиков:
1)В качестве графического образа лучше использовать линейные, круговые, столбиковые диаграммы, которые имеют наибольшую наглядность и доходчивость.
2)Графические образы располагаются слева направо, масштабные ориентиры графика по горизонтальной оси располагаются снизу, а по вертикали – с левой части графика.
3)Следует включать все исходные данные. Если это нецелеобразно, то исходные данные должны в табличной форме сопровождать график.
4)Все буквенные и цифровые значения должны располагаться так, чтобы их легко можно было отсчитывать от начала масштабной шкалы. Ряды цифровых данных по времени размещаются в строгой хронологической последовательности и обязательно по оси абсцисс.
5)Факторные признаки должны размещаться по горизонтальной оси и читаться слева направо, а результативные признаки – по вертикальной шкале и читаться снизу вверх.
6)Заголовок графика располагается под графиком. При этом сначала пишется «Рис. 1.», номер не указывается, и на этой же строке пишется его заголовок, который должен быть кратким, и достаточно точно без двойного понимания отражать его основное содержание.
|
|
|
Статистический показатель, его состав, роль функции.
В стат.исследовании можно использовать один показатель, если явление не сложное; систему взаимосвязанных показателей, если явление сложное; обобщающие показатели (Эффективность=(∑прибыли/(З/п+Амортизация+Осн.Ср-ва))*100%)
Статистический показатель- обобщающая количественная характеристика признаков изучаемого явления по отдельным его частям или в целом в конкретных условиях пространства и времени, полученной на основании индивидуальных значений признака.
Содержание стат.показателя:
1. Определение сущности показателя(название)(ВВП)
2. Методика расчета показателя
3. Методика расчета тесно переплетается с единицей измерения
4. Количественная характеристика показателя зависит от ед.измерения и содержит в себе количественную часть. Должна указываться вместе с ед.измерения, - их может быть несколько для одного и того же явления.
Функции стат.показателя: каждый показатель несет определенную функциональную нагрузку
1)познавательная функция
2)стимулирующая
3)регулирующая
4)контрольная
Виды стат.показателей:
|
|
|
1)по сущности (объемные и качественные)
2)по степени агрегирования (индивидуальные или обобщающие)
3)по характеру изучаемого явления (моментные, интервальные)
4)по форме (абсолютные, относительные, средние, вариации (коллеблимости))
Показатель ограничивается: единицей измерения, объектом к которому относится, временем, местом действия.
Виды средних величин
Являются достаточно распространенной формой сводных показателей. Две группы средних:
1)средние степенные, которые используются для определения типического размера признака данной совокупности,
2)структурные средние (мода, медиана), которые используются для анализа рядов распределения и для спец.аналитических целей.
В практике экономики наиболее часто применяют 4 вида средних:
Простая или взвешенная
1.арифметическая при m=1
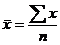
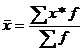
Размер величины средней не зависит от способа представления исходной информации (сгруппирована или нет).
2.средняя квадратическая при m=2
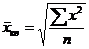
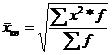
Область применения средне квадратического – для осреднения квадратной функции, а также для расчета показателей вариации в других спец.расчетах.
3.средняя гармоническая m=-1
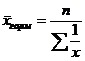
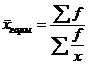
4.средняя геометрическая m=0
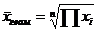, используется при расчете средних темпов изменения в динамических рядах и других экономич.расчетах.
Между всеми видами средних существуют след.соотношения – правило мажоритарности:
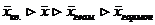
Дата добавления: 2018-02-15; просмотров: 594; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!