Критерии проверки и оценка решений задания 14
Задание 14 – стереометрическая задача, она разделена на пункты а и б. Для получения 2 баллов нужно, чтобы были выполнены оба пункта, а для получения 1 балла хватает выполнения одного из этих пунктов.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | 2 |
| Имеется верное доказательство утверждения пункта а ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
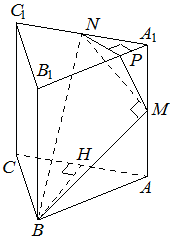
Задача 14 (демонстрационный вариант 2020 г.).
Все рёбра правильной треугольной призмы 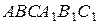 имеют длину
имеют длину  . Точки
. Точки 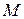 и
и  — середины рёбер
— середины рёбер 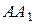 и
и 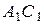 соответственно.
соответственно.
а) Докажите, что прямые  и
и 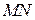 перпендикулярны.
перпендикулярны.
б) Найдите угол между плоскостями  и
и 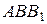 .
.
|
Решение. а) Пусть точка 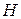 — середина
— середина 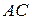 . Тогда
. Тогда
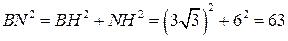 .
.
Вместе с тем
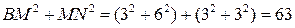 ,
,
а тогда по теореме, обратной теореме Пифагора, треугольник  является прямоугольным с прямым углом
является прямоугольным с прямым углом 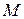 .
.
б) Проведём перпендикуляр  к прямой
к прямой  . Тогда
. Тогда  и
и 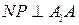 . Следовательно,
. Следовательно, 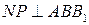 . Поэтому
. Поэтому 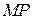 — проекция
— проекция 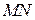 на плоскость
на плоскость  .
.
Прямая  перпендикулярна
перпендикулярна 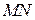 , тогда по теореме о трёх перпендикулярах
, тогда по теореме о трёх перпендикулярах 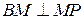 . Следовательно, угол
. Следовательно, угол 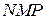 — линейный угол искомого угла.
— линейный угол искомого угла.
Длина  равна половине высоты треугольника
равна половине высоты треугольника  , то есть
, то есть  . Поэтому
. Поэтому 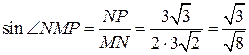 . Следовательно,
. Следовательно,  .
.
Ответ: б) 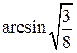 .
.
Задание 1
|
|
|
В правильной треугольной призме 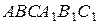 сторона
сторона  основания равна 6, а боковое ребро
основания равна 6, а боковое ребро 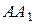 равно 3. На рёбрах
равно 3. На рёбрах  и
и 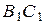 отмечены точки
отмечены точки 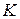 и
и 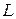 соответственно, причём
соответственно, причём  . Точка
. Точка 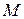 — середина ребра
— середина ребра 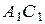 . Плоскость
. Плоскость 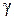 параллельна прямой
параллельна прямой 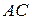 и содержит точки
и содержит точки 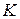 и
и 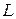 .
.
а) Докажите, что прямая 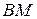 перпендикулярна плоскости
перпендикулярна плоскости 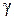 .
.
б) Найдите объём пирамиды, вершина которой — точка 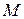 , а основание — сечение данной призмы плоскостью
, а основание — сечение данной призмы плоскостью 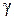 .
.
Решение.
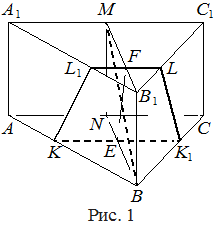
а) Проведём через точки 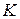 и и 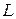 прямые, параллельные прямые, параллельные 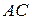 . Пусть эти прямые пересекают рёбра . Пусть эти прямые пересекают рёбра 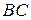 и и 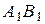 в точках в точках  и и 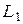 соответственно (рис. 1). Тогда трапеция соответственно (рис. 1). Тогда трапеция 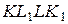 является сечением исходной призмы плоскостью является сечением исходной призмы плоскостью 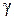 . Рассмотрим плоскость . Рассмотрим плоскость 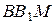 . Пусть эта плоскость пересекает прямые . Пусть эта плоскость пересекает прямые 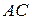 , , 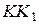 и и 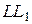 в точках в точках  , , 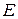 и и  соответственно. Четырёхугольник соответственно. Четырёхугольник 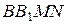 — прямоугольник, причём — прямоугольник, причём 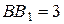 , ,  . .
| 
|
Кроме того, 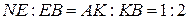 ,
, 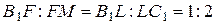 , откуда
, откуда  ,
,  . Пусть
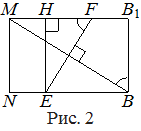
. Пусть 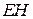 — высота трапеции
— высота трапеции 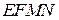 (рис. 2), тогда
(рис. 2), тогда
 .
Поскольку .
Поскольку 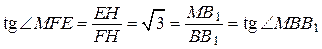 , ,
 ,
то есть прямые ,
то есть прямые 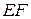 и и 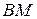 перпендикулярны. перпендикулярны.
| 
|
Прямая 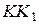 параллельна прямой
параллельна прямой 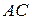 , которая перпендикулярна плоскости
, которая перпендикулярна плоскости 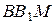 . Значит, прямые
. Значит, прямые 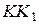 и
и 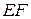 перпендикулярны прямой
перпендикулярны прямой 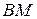 , поэтому прямая
, поэтому прямая 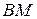 перпендикулярна плоскости
перпендикулярна плоскости 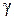 .
.
б) Расстояние от точки 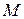 до плоскости
до плоскости 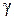 равно
равно 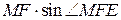 , а площадь трапеции
, а площадь трапеции 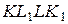 равна
равна
 .
.
Значит, искомый объём равен  .
.
Ответ: б)  .
.
Задание 2
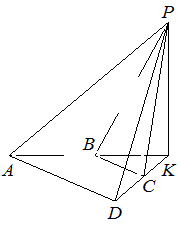
Основанием четырёхугольной пирамиды 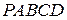 является трапеция
является трапеция 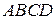 , причём
, причём 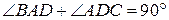 . Плоскости
. Плоскости  и
и 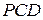 перпендикулярны плоскости основания,
перпендикулярны плоскости основания, 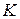 — точка пересечения прямых
— точка пересечения прямых 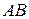 и
и  .
.
|
|
|
а) Докажите, что плоскости  и
и 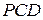 перпендикулярны.
перпендикулярны.
б) Найдите объём пирамиды 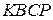 , если
, если  , а высота пирамиды
, а высота пирамиды 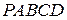 равна 9.
равна 9.
Решение.
|
а) Заметим, что 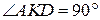 . Плоскости
. Плоскости  и
и 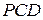 перпендикулярны плоскости основания, поэтому они пересекаются по прямой, содержащей высоту пирамиды. Значит,
перпендикулярны плоскости основания, поэтому они пересекаются по прямой, содержащей высоту пирамиды. Значит,  — высота пирамиды. Таким образом, угол
— высота пирамиды. Таким образом, угол 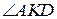 является линейным углом двугранного угла между плоскостями
является линейным углом двугранного угла между плоскостями  и
и 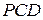 . Значит, они перпендикулярны.
. Значит, они перпендикулярны.
б) Поскольку 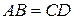 , трапеция
, трапеция 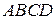 является равнобедренной. Значит,
является равнобедренной. Значит,
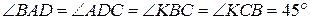 ;
;
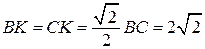 .
.
Таким образом, площадь треугольника 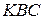 равна
равна 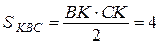 ,
,
а объём пирамиды 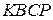 равен
равен 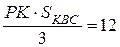 .
.
Ответ: б) 12.
Задание 3
В правильной четырёхугольной пирамиде 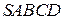 сторона основания
сторона основания 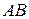 равна 6, а боковое ребро
равна 6, а боковое ребро 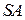 равно 7. На рёбрах
равно 7. На рёбрах  и
и 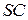 отмечены точки
отмечены точки  и
и 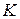 соответственно, причём
соответственно, причём 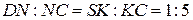 . Плоскость
. Плоскость 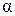 содержит прямую
содержит прямую 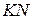 и параллельна прямой
и параллельна прямой 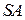 .
.
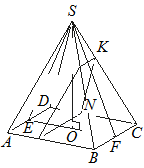 Рис. 1
Рис. 1
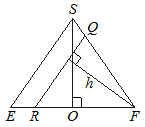 Рис. 2
Рис. 2
|
а) Докажите, что плоскость 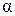 параллельна прямой
параллельна прямой 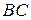 .
.
б) Найдите расстояние от точки  до плоскости
до плоскости 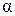 .
.
Решение.
а) По условию  , значит, прямые
, значит, прямые 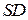 и
и 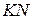 параллельны. Следовательно, плоскости
параллельны. Следовательно, плоскости  и
и 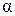 параллельны (рис. 1).
параллельны (рис. 1).
|
|
|
Поскольку отрезки 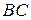 и
и 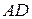 параллельны, а плоскость
параллельны, а плоскость 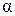 параллельна плоскости
параллельна плоскости  , прямая
, прямая 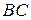 параллельна плоскости
параллельна плоскости 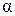 .
.
б) Поскольку плоскость 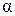 параллельна прямой
параллельна прямой 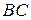 , расстояние от точки
, расстояние от точки  до плоскости
до плоскости 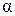 равно расстоянию от прямой
равно расстоянию от прямой 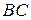 до плоскости
до плоскости 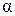 . Пусть точки
. Пусть точки 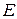 и
и  — середины рёбер
— середины рёбер 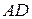 и
и 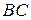 соответственно. Тогда прямые
соответственно. Тогда прямые 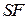 и
и 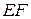 перпендикулярны прямой
перпендикулярны прямой 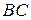 . Таким образом, плоскость
. Таким образом, плоскость 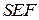 перпендикулярна прямой
перпендикулярна прямой 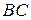 и параллельной ей плоскости
и параллельной ей плоскости 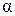 . Пусть плоскость
. Пусть плоскость 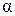 пересекает прямые
пересекает прямые 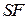 и
и 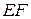 в точках
в точках 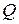 и
и  соответственно (рис. 2). Тогда искомое расстояние равно расстоянию
соответственно (рис. 2). Тогда искомое расстояние равно расстоянию 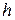 от точки
от точки  до прямой
до прямой 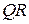 . Высота
. Высота 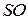 пирамиды
пирамиды 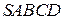 лежит в плоскости
лежит в плоскости 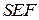 , откуда
, откуда
 ,
, 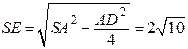 ;
; 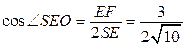 .
.
Плоскости  и
и 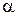 параллельны, поэтому
параллельны, поэтому  , откуда
, откуда
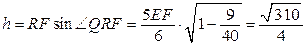 .
.
Ответ: б) 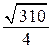 .
.
Дата добавления: 2021-04-05; просмотров: 56; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
