Краткий анализ основ геометрий 34 страница
В данной работе не будем останавливаться на методах гармонического проектирования и строительства, кое-что об этом можно найти в [23], здесь же качественно познакомимся с некоторыми проективными способами проведения пропорционирования фигур на плоскости и в пространстве. При этом надо помнить, что исходным пунктом всякого гармоничного пропорционирования является использование золотых пропорций. Гармоничное пропорционирование это всегда пропорционирование на основе золотых пропорций. В проекте строительства объекта высота, ширина и длина должны быть выполнены пропорционально золотому числу или золотым числам, т.е. в соответствии с методом проектирования на основе древнерусских саженей.
Остановимся на возможности гармонизации фигур в статико-динамической геометрии. Еще раз отметим, что в проективной полудинамической геометрии фигуры пропорционированы изначально как системы, способные кадрировано деформироваться в процессе перемещения в пространстве. И хотя все деформации будут постоянно происходить пропорционированно, и каждый кадр изменения фигуры, например, четырех точек, в движении называют гармоничным, это не всегда соответствует действительности. Гармоничное пропорционирование деформации элементов каждого кадра фигуры происходит только тогда, когда высота и ширина (для плоскости), и длина (для объема) исходной фигуры проектировались по соизмерительным инструментам, содержащим золотые числа. Все другие пропорции не приводят к получению гармоничного отношения. Поскольку объемное пропорционирование по золотым пропорциям еще не устоялось и не применяется в проективной и начертательной геометрии, разберем несколько примеров пропорционирования фигур на плоскости.
|
|
|
Основная задача статико-динамической геометрии – нахождение элементов фигур, пропорционированных в золотых числах, и обеспечение возможности перенесения этих пропорций на любой элемент внешней фигуры. Выше показаны два способа проведения гармонического пропорционирования как отрезка АВ, так и базисной прямой точками N и М: методом пирамиды Дезарга и методом параллельных Евклида. Оба способа дают аналогичные результаты и отличаются лишь трудоемкостью их исполнения. Оба способа начинаются с выбора отрезка АВ и деления его в произвольном отношении точкой N – следом поляры. И только две точки на этом отрезке могут обусловить появление золотых пропорций. Естественно, что в проектировании фигур или объектов эти точки могут проявить себя только при целенаправленном выборе. Не останавливаясь на описании использования золотых пропорций, приведем пример пропорционированого переноса в пространстве плоской фигуры.
|
|
|
Рассмотрим построение на поверхности плоской или объемной фигуры и передвижение ее в пространстве способом пропорционирования. Проведем базисную прямую р и выделим на ней отрезок АД, который произвольно разделим на три части точками В и С (рис. 68). Получили некоторый аналог четырех гармонических точек. Поставим произвольную точку S, соединим ее лучами с точками А, В, С, Д, и посмотрим, что же получилось. Можно предположить, что здесь изображена проективная пирамида в которой точка В проекция поляры на базисную прямую, а точка Д полюс этой поляры. Однако для такой остроконечной фигуры полюс находится неестественно близко. Можно сделать другое предположение: фигура составлена из двух пересекающихся проективных пирамид АSВ и ВSД, каждая из которых включает поляру, а полюса у них – отсутствуют. Наконец возможен и третий вариант: на фигуре изображена четырехгранная пирамида, находящаяся на горизонтальной плоскости.
Допустим, что это четырехгранная пирамида и в произвольном месте пересечем ее плоскостью. Пронумеруем углы образовавшейся площадки 1, 2, 3, 4, и обратим внимание на то, что каждая сторона полученного четырехугольника образует со сторонами пирамиды трапеции: А12В, В23D, D34С, С41А. Выше было показано, что продолжение крыши каждой трапеции пересекает базисную прямую, образуя на ней свой полюс. Появление полюса свидетельствует о том, что внутри каждой трапеции существуют диагонали, а вместе с ними и виртуальная поляра. Проявим поляру, например, у ребра АSВ, для чего проведем в трапеции диагонали и через их пересечение проведем прямую – поляру SL (показано штрихами). Далее проведем лучи от крыш до пересечения базисной прямой в точках Е, F, G, Н и отметим, что любое наклонение пирамиды сопровождается деформацией всех ее элементов, но точки полюсов при этом своего положения не меняют и потому становятся реперами. Воспользовавшись этим обстоятельством, поставим произвольно новую точку опоры Sо. Соединим ее прямыми с точками А, В, С, D и перенесем на нее площадку 1234. Перенос можно произвести двумя способами: произвольным способом и пропорционально занимаемому ею месту. Для получения площадки по первому способу следует в нужном месте поставить на одно из ребер наклонной пирамиды АSоD точку, например, 1´ и, соединив ее лучами с реперами Е и G´, получить стороны 1´2´ и 1´4´. Далее соединив лучами точку 2´ с репером F и точку 3´ с репером Н получить стороны 2´3´ и 3´4´. Искомая площадка 1´2´3´4´ построена.
|
|
|
Чтобы оставить все элементы пирамиды АSоD пропорциональными АSD, необходимо провести две вспомогательные прямые. Одной соединить вершины S и S1, а другую S1K – провести перпендикулярно первой. Затем перпендикулярно прямой SоK перенести с пирамиды АSD точки 1, 2, 3, 4 на ребра пирамиды АSоD получить точки 11, 21, 31, 41 и соединив их прямыми, найти искомую площадку. Можно наклонить пирамиду и вправо, например, в точку опоры S1 провести построение пирамиды аналогично вышеизложенному.
|
|
|
Может возникнуть необходимость пропорционального перенесения площадки 1234 под базисную плоскость пирамиды. Поскольку первая точка искомой площадки может выбираться произвольно, ее ставят на продолжении любого ребра, например, точку 2о на продолжении ребра SВ и лучами соединяют с реперами Е и Н (рис. 68). Лучи пересекают продолжения ребер АS и SD в точках 1о и 3о. Теперь, соединяя лучами точки 1о и G, получаем точку 4о, соединив ее с точкой 1о, находим искомую площадку 1о2о3о4о. Полученная площадка является видом сверху с базисной плоскости.
Пространственное пропорционирование и перенос плоских и объемных фигур в рамках пирамиды хорошо известен и применяется в начертательной геометрии. Но в ней используется метод пропорционирования относительно сдвинутой базисной прямой или плоскости.
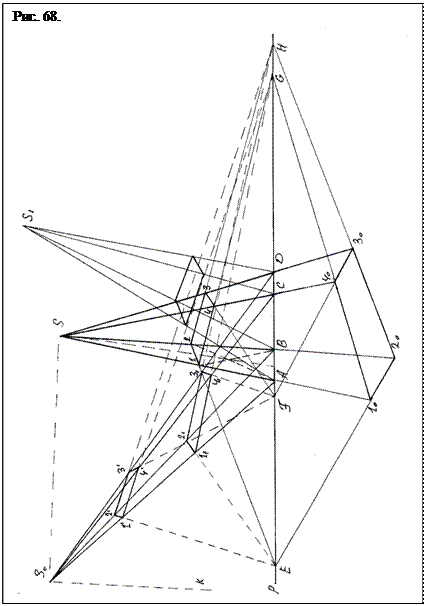
Реперный способ пропорционирования, похоже, неизвестен и не применяется. Естественно, что фигуры, пропорционированные обоими методами, должны быть конгруэнтными. Покажем это на примере пропорционирования той же площадки 1234.
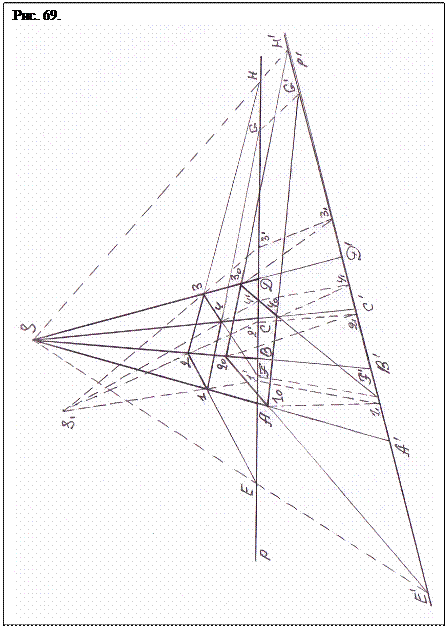
На базисной плоскости р построим прямоугольную пирамиду с основанием АВСD и с вершиной S (рис. 69). Рассечем ее плоскостью 1234. Каждое ребро плоскости можно представить как крышу некоторой трапеции. Перенесем лучами на базисную поверхность р реперные точки Е, F, G, Н, от каждой крыши. Поведем другую базисную плоскость р´ и продолжим грани пирамиды до пересечения с нею в точках А´, В´, С´, D´. Проведем через вершину S и точки Е, F, G, Н лучи до пересечения с р´ в точках Е´, F´, G´, Н´. Реперные отметки перенесены на новую базисную плоскость.
Теперь можно поступать двумя способами: либо, как это изложено в начертательной геометрии, выбрать произвольную вершину S1 и провести от нее лучи до пересечения с р. Либо сразу же поставить на одно из ребер пирамиды какую-то точку плоскости, например 1. Выберем вершину S1 и проведем от нее лучи (показано штрихами) через точки 1, 2, 3, 4 до пересечения с р в точках 1´, 2´, 3´, 4´. Потом из вершины S проведем лучи через точки 1´, 2´, 3´, 4´ до пересечения с плоскостью р´ в точках 11, 21, 31, 41. Возможность пропорционального перенесения площадки 1234 на другое место подготовлена. Теперь соединим лучам точку S1 с точками 11, 21, 31, 41 и пересечение их с ребрами А´S, В´S, С´S, D´S пронумеруем точками 1о, 2о, 3о, 4о. Соединив полученные точки прямыми получим искомую площадку 1о2о3о4о. Теперь через точки 2о и 1о, проведем луч до пересечения с плоскостью р´. Луч пройдет через репер Е´. Проведя аналогичную операцию с точками 2о и 3о, получим репер Н´, с точками 3о и 4о, получим репер F´, с точками 1о и 4о, получим репер G´ (показано на рис. 69 штрихами.).
Таким образом, «площадки» 1о2о3о4о, перенесенная методом начертательной геометрии и методом реперов, оказываются конгруэнтными.
Не будем останавливаться на пропорционировании объемных фигур методом реперных отметок, поскольку он в принципе повторяет способ пропорционирование плоскостей. Покажем в заключение метод гармоничного пропорционирования вынесенных на оптимальное расстояние за начальную фигуру других плоских или объемных фигур. Этот метод существенен потому, что на сегодня, похоже, отсутствует способ перенесения одной фигуры пропорционально другой и гармоничного сочетания объектов по площади, высоте и объему.
Поэтому застройки городов по высоте, расположению в пространстве и конфигурации объектов представляют безобразное, ангармоничное нагромождение строений, уродующее структуру Земли и разлагающе действующее на психическое здоровье человека.
Еще раз отметим, что гармоничными сооружениями считаются такие объекты, которые по высоте, ширине и длине пропорционированы в золотых пропорциях. Пространственное размещение гармоничных объектов предполагает также использование не измерительных, а соизмерительных инструментов, тех же саженей, как для архитектурного проектирования, так и для размещения их на местности.
Покажем на одном примере пропорциональное перемещение фигуры с одного места на другое, расположенное рядом. Для этого отложим на базисной прямой отрезок АВ = 6 см и разделим его точками А, В, N, D на три части (рис. 22.), причем точка N делит АD в крайнем и среднем отношении. Из точки N восстановим перпендикуляр – поляру, на которой определяем точку опоры S отстоящую от основания на величину, например, равную 9 см. Соединив точку S с точками А и D находим пирамиду АSD, по которой и будет пропорционирована соседняя фигура. Далее следует определить расстояние от пирамиды до соседней фигуры. Оно должно быть кратным золотому числу, например АВ : 2,618 = 3,5 см.
Построение пропорционированной фигуры, отнесенной от пирамиды на расстояние 3,5 см, начинаем с проведения второй базисной прямой р´, параллельной первой. Поскольку предстоит пропорциоро- ванный «переход» пирамиды АSD на новое место, то следует эту пирамиду «наклонить», перенеся ее точку опоры, например, в точку Sо. И из нее через точки А, В, N, D провести лучи до пересечения с р´ в точках А´, В´, N´, D´. Теперь отложим от точки А отрезок АDо = 3,5 см и через точку Dо из точки D´ проведем луч, на котором в произвольном месте поставим опорную точку S1. Соединим точку S1 лучами с точками А´, В´, N´ и в месте пересечения р´ получим точки Ао, Во, Nо основания наклонной пирамиды АоS1Dо. Искомая пирамида АоS1Dо пропорциональна по вурфу пирамиде АSD. Это можно показать графически. Ранее было показано, что лучи от крыш всех трапеций пропорционированных по вурфу пирамид сходятся в одной точке М. Найдем эту точку для пирамиды АSD. Для этого на поляре возьмем произвольную точку К и от А и D проведем через нее лучи до пересечения с ребрами АS и SD в точках Е и F. Прямая EF − крыша, спроектируем ее на базисную прямую р и получим полюс М. Отметим, что для всех пропорционированных пирамид расстояние от правой точки опоры до полюса будет всегда одинаковым и равным DМ.
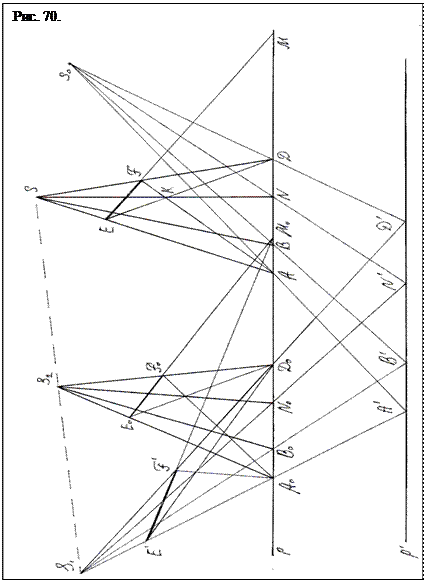
Чтобы убедиться в этом построим аналогичную крышу для пирамиды АоS1Dо и продолжим ее до пересечения с р в точке Мо. Замерим отрезок DоМо и получаем, что расстояние ДМ = DоМо. Дополнительно проверим это явление. Поставим еще одну точку опоры S2 и соединив ее сточками Во, Dо получаем еще одну пирамиду пропорциональную А1S2Dо. Определим на ней крышу ЕоFо проведем от нее луч до пересечения с р. Луч пересек р в точке Мо. Таким образом вурфную пропорциональность пирамид АоS1Dо и АSD можно считать доказанной.
Кратко рассмотрим особенности фигуры называемой «теорема Паскаля». Вот как она описывается [27]:
«Впишем в любое коническое сечение (для проективной геометрии разницы между ними нет) произвольный (произвольный?? – Авт.) шестиугольник (см. рис. 71, на котором стороны занумерованы). Продолжим теперь до пересечения первую и четвертую, вторую и пятую, третью и шестую стороны. Полученные прямые обязательно пересекутся, ибо параллельных в проективной геометрии нет (?? − достаточно сомнительное заявление − Авт.). Итак, мы имеем три точки пересечения трех пар прямых. Вообще говоря, три произвольные точки плоскости не лежат на одной прямой, но эти три − лежат. В этом и заключается теорема Паскаля. Если теперь проектировать коническое сечение вместе с шестиугольником, с точками пересечения его сторон и с прямой, проходящей через эти три точки (ее называют паскалевой прямой), на другую плоскость, то, как бы не изменялось коническое сечение и вся конфигурация, указанные три точки все равно будут лежать на одной прямой. Теорема Паскаля – проективная теорема».
Фигура, изображенная на рис. 71, чуть ли не единственная в проективной геометрии явно отображающая все входящие в ее структуру элементы. А изложенное объяснение ее построения демонстрирует односторонность современного статического подхода к рассмотрению образовавшейся фигуры. Математик, построивший в коническом сечении шестиугольник, полагает, что за пределами шестиугольника ничего нет. И это совершенно правильно, если фигура принадлежит статической геометрии. Но если она относится к проективной геометрии, то сама фигура «знает», что она всего только базисный, опорный элемент единой невидимой фигуры. Вторым элементом является базисная прямая, проходящая за ее пределами и потому попарные лучи, продолженные за пределы сторон шестиугольника обязательно пересекутся на базисной прямой.
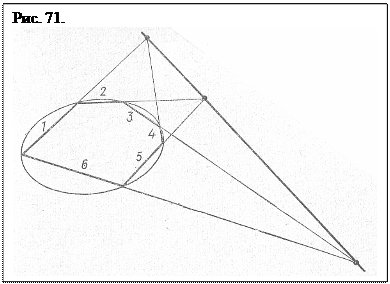Тольков проективном представлении субъекта вписанный в коническое сечение шестиугольник (далее, для упрощения, будем говорить об окружности), является самостоятельной фигурой. В статико-динамической геометрии это несколько неявных фигур-треугольников. Они, частично перекрывая друг друга, наложены на опорную окружность, отсекая своими сторонами шесть хорд, образующих шестиугольник, и составляя вместе с базисной прямой, единую фигуру.
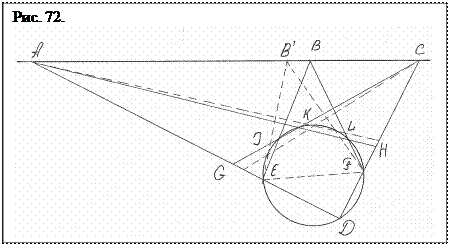
Проведем построение вписанного шестиугольника иначе, чем было описано выше. Возьмем опорную окружность и на некотором расстоянии от нее базисную прямую, на которой находятся точки А, В, С. На окружности расположена точка D, место схождения двух сторон шестиугольника (рис. 72.).
Соединим точки А и С прямыми с точкой D. Точки пересечения Е и F прямых с окружность соединим прямыми с точкой В. Получим новые точки I и L. Из точки С через точку I проведем прямую до пересечения с прямой АD в точке G. А из точки А прямую через L до пересечения с прямой СD в точке Н. Точка пересечения этих прямых К окажется на окружности и замыкает шестигранник. Шестигранник DЕIКLF построен. Он составлен тремя треугольниками АDН, ВFЕ, СDG. Стороны этих треугольников, проходящие внутри окружности, и образуют искомый шестигранник. Он весь включен в треугольник АСD и одновременно, отсекаемыми хордами, вписан в опорную окружность.
Перемещение любого из элементов этой фигуры сопровождается деформацией всех ее элементов кроме базисных. Они же, оставаясь базисными, не испытывают деформации. Базисные фигур испытывают деформацию только тогда, когда перемещаются в другую область пространства. Именно в этом случае окружность, например, отображает коническое сечение.
Покажем деформацию треугольников АНD ВFЕ, и СDG обусловленную перемещением точки В вдоль базисной прямой, допустим влево (показано штрихами). Перемещение В оставило неизменным треугольник АСD и основание треугольника ВFЕ но переместила одну из их сторон (показано штрихами), изменив площадь каждого внутреннего треугольника и точки их пересечения таким образом, что четыре стороны вписанного шестиугольника переместившись по окружности, изменили свою длину, а следовательно, и конфигурация шестиугольника подверглась изменению. Перемещение же точек А и С вдоль базисной прямой, «удаление» или «приближение» к ней опорной окружности, вызывает деформацию всех элементов фигуры, но не сдвинет «произвольные» точки с паскалевой прямой, поскольку эта прямая – базисная.
Таким образом, деформация фигуры в пространстве статико-динамической геометрии, происходящая в результате перемещения отдельных ее элементов или опорных узлов не нарушает структурного единства самой фигуры. Пединим прямыми с точкой В.кружность льника., В, С. описано выше.
Дата добавления: 2021-02-10; просмотров: 70; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!