Краткий анализ основ геометрий 32 страница
4.3. Числа Фибоначчи и
золото статико-динамической геометрии
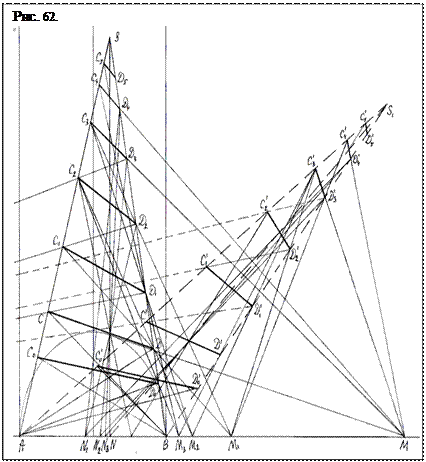
Предположим, в качестве примера, что в своем движении от центра круга к точке В поляра «случайно» заняла положение, соответствующее делению диаметра АВ золотым сечением, и пирамида стала асимметричной, как показано на рис.62 Часть структуры элементов фигур образуемая золотым сечением, как уже отмечалась выше, оказывается пропорциональной золотому числу. Поскольку основание пирамиды равно 10 см, то поляра разделяет его на две части длиной 6,1803 см больший отрезок и 3,8197 см - меньший. Поляра высотой 19 см пересекает семь этажей крыш, расстояния между которыми в см равны: 2,05; 2,8; 3,25; 2,95; 2,15; 1,3. Как и в симметричной пирамиде, расстояние между крышами остается неодинаковым, следствие анизотропности плотностного пространства пирамиды. Однако физическая пропорциональность между ними сохраняется, что и подтверждается коэффициентом вурфа, найденным по уравнению (4.2):
W1 = 1,286; W2 = 1,282; W 3 = 1,284; W4 = 1,287.
Передвижение поляры из центра окружности вызвало наклонение крыш трапеций в сторону В, и лучи от них сходятся на точке М. В этой же точке базисную прямую пересекает касательная, исходящая от окружности в точке пересечения ее полярой. А это значит, что имеет место гармоническая четверка точек, определяемая равенством:
АN ⁄ВN = АМ ⁄ВМ
Решаем это равенство и получаем следующие величины образовавшихся отрезков: АМ = 26,18 см; ВМ = 16,18 см. Отрезок АМ по модулю равен десяти квадратам золотого числа Ф2 = 2,618, а отрезок ВМ по модулю равен десяти золотым числам Ф1 = 1,618. Числа эти существуют не сами по себе. Они члены числовой последовательности степенного греческого ряда, в котором каждый последующий член равен их сумме:
|
|
|
Ф1 + Ф2 = Ф3 = 1,618 + 2,618 = 4,236. (4.4)
Здесь модуль величины Ф в степени определяет собой размерностную длину двух отрезков, а их сумма – длину всего отрезка.
Аналогично для модулей АМ и ВМ имеем:
1а) ВМ + АМ = С1Д1 = 16,18 + 26,18 = 42,36. (4.5)
Таким образом, пропорции четверки гармонических чисел проективной геометрии есть геометрическое отображение процесса нарастания (последовательного сложения) произвольных начальных величин чисел ряда Фибоначчи (метод сложения Фибоначчи).
Отметим, что такого типа суммирование в проективной геометрии не производится, хотя получение четырех точек достигается тем же способом, т.е. делением отрезка, отграниченного двумя точками, на два отрезка. Отношения получившихся отрезков и определяют гармоничность трех точек. В нашем случае это точки А, N, В.
Отрезки АN и ВN вместе и составляют отрезок АВ. Однако, повторимся, операция аналогичная сложению модулей отрезков АМ и ВМ как и отрезков АN и ВN в проективной геометрии не проводится. Проведем ее:
|
|
|
1б) ВN + АN = АВ = 3,8197 + 6,1803 = 10,00. (4.6)
То, что величина АВ равна сумме ВN и АN, понятно и без записи равенства (4.6) поскольку именно АВ делилась в крайнем и среднем отношении. Но операция сложения полученных модулей отрезков, это не операция деления, а процесс выявления числовой структуры получаемых пропорций. Она-то и определяет факторы, обусловливающие гармоничность четырех точек, рассматриваемых в проективной геометрии, и бесконечного количества точек базисной прямой, которые появляются в статико-динамической геометрии. Именно поэлементное сложение (4.5) и (4.6) определяет структуру всех гармонических чисел и их взаимосвязь с золотыми пропорциями. И сумма отрезков как самостоятельная величина для данной фигуры, пропорциональная Ф3, в (4.4), (4.5), (4.6) она, похоже, не употребляется в проективной геометрии.
Операции сложения:
АN + ВN = АВ,
АМ + ВМ = С1Д1,
являются важнейшими операциями статико-динамической геометрии. Эти операции изначально предполагают потенцию непрерывного движения, поскольку производятся по правилу Фибоначчи, которое обусловливает бесконечное последовательное сложение двух чисел, при этом каждый последующий член ряда равен сумме двух предыдущих. Именно операция сложения модулей двух известных (АN и ВN) и двух неизвестных АМ и ВМ отрезков определяет начало ряда Фибоначчи и возможность гармонического пропорционирования четырех (многих) точек базисной прямой. Причем важнейшим обстоятельством пропорционирования является то, что в одно неизвестное число входит число известное, являющееся суммой двух известных чисел:
|
|
|
АМ = АВ + ВМ.
Этообстоятельство обусловливает пропорциональную на общий коэффициент взаимосвязь между известными и неизвестными длинами отрезков и, следовательно, возможность формализации одного уравнения с двумя неизвестными. В нем изначально закладывается пропорционирование как отношение неизвестных друг к другу через суммарное известное, входящее в неизвестное. Запишем это отношение:
АN ⁄ВN = (АВ +ВМ) ⁄ ВМ
И получаем уравнение из четырех членов с одним неизвестным ВМ. Преобразуя его, получаем:
ВМ = АВ·ВN ⁄ (АN – ВN). (4.7)
Следовательно, проекция поляры, в своем кадрированном движении вдоль диаметра, делит точками-полюсами базисную прямую на множество отрезков, гармонически пропорциональных его образовавшимся частям.
|
|
|
Если и в операциях (4.5) и (4.6) убрать знаки сложения и равенства, то перед нами два ряда начальных чисел Фибоначчи, сдвоенных в ряд Пилецкого. Сами по себе ряды Фибоначчи свидетельствуют об адекватности процессов, отображаемых ими отдельным природным зависимостям. Появление же ряда Пилецкого свидетельствует уже о наличии комплекса таких явлений, свидетельствует о развитии движения отдельных элементов во взаимосвязанную инвариантную систему, которая в дальнейшем вырождается в соответствующую матрицу. Модуль каждой тройки чисел (внутренних и внешних), двух слагаемых отрезков и результата, составляют ячейку из трех первых членов ряда А. Пилецкого. Двух рядов из трех чисел, каждый из которых в потенции последовательного сложения и умножения по вертикали на общий для них коэффициент в конечном итоге преобразуются в матрицу. В ряду Пилецкого числа одной строки отличаются от чисел другой на один и тот же коэффициент. Разделим каждое верхнее число на нижнее, и определим, связаны ли они единым коэффициентом:
16,18; 26,18; 42,36;
3,820; 6,180; 10,00;
коэффициент 4,236; 4,236; 4,236.
Коэффициент 4,236, единый для каждой пары чисел свидетельствует о том, что данный набор чисел есть сдвоенный ряд Пилецкого. Появление единого коэффициента пропорциональности между модулями параметров в пределах отрезка и с ним за его пределами в виде ряда Пилецкого обусловливает гармоничность множеству точек статико-динамической геометрии. Покажем развитие ряда Пилецкого посредством последовательного сложения чисел по горизонтали и умножения верхнего ряда на 4,24 и деления нижнего на те же 4,24 по вертикали (матрица 2).
Матрица 2
… … … … … …
… 42,37 68,53 110,9 179,4 290,3 …
… 10,00 16,18 26,18 42,36 68,54 …
… 2,360 3,820 6,180 10,0 16,18 …
… 0,557 0,902 1,459 2,361 3,820 …
… … … … … … …
В результате получаем, что сдвоенный ряд Пилецкого, образованный четверкой гармонических точек, является фрагментом одной из золотых русских матриц. Она изначально базируется на золотой пропорции и имеет следующие золотые коэффициенты взаимосвязи:
По строкам слева направо Ф1 – 1,618,
По диагонали слева направо сверху вниз Ф2 – 2,618.
По столбцам снизу вверх Ф3 – 4,236,
По диагонали слева направо снизу вверх Ф4 – 6,854,
Отметим одну существенную особенность фрагмента этой матрицы. Продолжим ряды Пилецкого за пределы фрагмента влево и вправо:
… 1,46; 2,36; 3,82; 6,18; 10,0; 16,18; 26,18; 42,36; 68,54; …
… … ; … ; … ; 1,46; 2,36; 3,82; 6,180; 10,00; 16,18; …
И оказывается, что здесь наличествует последовательность чисел одного ряда, сдвинутого относительно друг друга на три числа. Эта операция сдвижения рядов, по-видимому, возникает потому, что поляра разделяет диаметр (или отрезок) в крайнем и среднем отношении. (Известно, что сдвиг числовых строк натурального ряда обусловливает и появление мифических квадратов.) Матрицы данного типа (русская матрица со сдвинутой строкой) образуют группу золотых многобазисных матриц и, похоже, наиболее адекватно отображают структуру окружающего космического пространства. В матрице базисная единица отображает плотностное пространство, которое в окружающем космическом пространстве представляют, например, планеты, звезды, галактики. Пропорциональность же чисел обеспечивает коэффициент пропорциональности – свой для каждого сдвоенного ряда. Выше показано, что всякое динамическое развитие проходит начальную стадию (последовательность) формирования рядов Фибоначчи с выходом на ряды Пилецкого и в дальнейшим с переходом в один из вариантов русской матрицы.
Покажем, что остальные точки серий М и N образуют подобные сдвоенные тройки чисел, которые могут формировать такие же фрагменты. По методу, описанному выше, находим несколько точек серий М и N и последовательно по уравнению (4.5)–(4.6) определяем расстояние их от точек А, В и N для проективной пирамиды рис. 62. Поскольку операция по нахождению расстояния до этих точек достаточно проста, проводить ее не будем, а, просто замерив и выписав полученные при построении расстояния до трех точек каждой серии в см, попробуем определить возможность взаимного пропорционирования их модулей: ВМ1 = 4,52; АМ1 = 14,52; ВN1 = 2,32; АN1 = 7,63; ВМ2 ==1,75; АМ2 = 11,75; ВN2 = 1,3; АN2 = 8,7; Это параметры точек расположенных по правую сторону от поляры (рис.62). Выпишем аналогичные параметры точек расположенных по левую сторону от поляры: АМ´ = 42,32; ВМ´ = 55; АN´ = 4,5; ВN´ = 5,5; АМ´´ = 11,67; ВМ´´ = 21,67; АN´´ = 3,5; ВN´´ = 6,5; АМ´´´ = 6,91; ВМ´´´ = 16,91; АN´´´ = 2,9; ВN´´´ = 7,1.
Отметим, что каждая из получаемых точек серий М отсекает на базисной прямой отрезок некоторой длины, пропорциональный определенным отрезкам, отсекаемым точками серии N на диаметре. Поэтому имеется возможность привести попарно сложение модулей величин этих отрезков, приводя их к виду (4.5)-(4.6).
Пары справа от поляры:
2а) ВМ1 + АМ1 = С2Д2 = 19,04; 2б) ВN1 + АN1 = АВ = 10. (4.8)
3а) ВМ2 + АМ2 = С3Д3 = 13,50; 3б) ВN2 + АN2 = АВ = 10. (4.9)
Пары слева от поляры:
1) АМ´ + ВМ´ = С1´Д1´ = 100; 1´) АN´ + ВN´ = АВ = 10. (4.10)
2) АМ´´ + ВМ´´ = С2´Д2´ = 33,34; 2´) АN´´ + ВN´´= АВ = 10. (4.11)
3) АМ´´´ + ВМ´´´ = С3´Д´3 = 23,82; 3´) АN´´´ + ВN´´´= АВ = 10. (4.12)
Еще раз отметим, что пропорциональность сдвоенных рядов обеспечивает коэффициент, получаемый делением каждого верхнего числа на нижнее. В частности, для ряда 3)-3´) этот коэффициент равен 2,382. Каждый последующий член ряда, по методу Фибоначчи, равен сумме двух предыдущих. А отношение двух соседних чисел ряда синхронно приближаются к Ф. Таблица 5 отображает эту синхронность. Приближение к числу Ф показано и над числами первого ряда, и под числами второго ряда.
Таблица 5
2,447; 1,408; 1,710; 1,585; 1,631; 1,6131; 1,6199; 1,617
6,91; 16,91; 23,82; 40,73; 64,55; 105,28; 169,83; 275,11; 444,94;
2,9; 7,1; 10; 17,1; 27,1; 44,2; 71,3; 115,5; 186,8;
2,448; 1,408; 1,710; 1,585; 1,631; 1,6131; 1,6199; 1,617
Внутреннее родство сдвоенных рядов подтверждается и методом вурфа. Если в уравнение (4.2) подставить числа парных рядов, то для каждой пары будет получен одинаковый вурфный коэффициент. Покажем это для пропорции образуемой с точками М и N:
W 1а = (ВМ + АМ) (АМ + С1Д1) ⁄АМ(ВМ + АМ + С1Д1) = 1,309 = Ф2⁄2.
W 1б= (ВN + АN) (АN + АВ) ⁄(ВN + АN + АВ) = 1,309 = Ф2⁄2.
Найдем попарные вурфы других рядов:
W2а= 1,156; W2б= 1,155; W3а = 1,074; W3б = 1,074;
W1 = 1,409; W1´ = 1,409; W2 = 1,269; W2´= 1,269;
W3 = 1,074; W3´ =1,074.
Разная величина вурфных отношений, каждая для своей пары, тем не менее, не препятствует, как будет показано далее, пропорционированию всех точек в единую взаимосвязанную комбинацию. Отметим, однако, что пропорциональные отсекаемым отрезкам величины серии СД, являющиеся параметрами некоторых неявных гармонических точек на базисной прямой, вообще не используются в проективной геометрии. Это обстоятельство скрывает объективную пропорциональность всей системы образуемых отрезков и их попарную аналогию с первой тройкой чисел рядов Фибоначчи. Кроме того, наличие этих рядов свидетельствует о том, что образующаяся система пропорциональных гармонических отрезков отображает динамические процессы в проективной геометрии. Как явствует из (4.5)-(4.6) любое статическое положение поляры на диаметре фигуры обусловливает появление некоторой серии гармонических точек отсекающих на базисной прямой, за пределами окружности, симметричные и несимметричные попарно пропорциональные отрезки. Последние и формализуются в виде (4.7). С проявлением парных пропорций и с возрастанием количества точек на базисной прямой значительно расширяется структура пропорционирования отрезков.
Как уже было показано, основное уравнение гармонической четверки точек в проективной геометрии имеет следующий вид:
АN ⁄ ВN = АМ ⁄ ВМ
Оно может преобразовываться в следующую форму:
АN·ВN ⁄АМ·ВN = 1. (4.13)
Отметим, что отношение (4.13) – многозначная пропорциональность, приравненная базисной 1, – основа памяти чисел и теории физической размерности. Она обусловливает нахождение любого неизвестного члена уравнения по трем известным. Базисная единица есть безразмерностная константа в математике, и в частности особым (центральным или базисным) числом в русской матрице, а в физике может быть как размерностной, так и безразмерностной единицей, связывающей переменные параметры одной системы. Именно она отображает динамику (бесконечное движение) свойств одной системы как в статико-динамической, так и физической (динамической) геометрии. Пропорциональное изменение переменных параметров в аналогичной форме физических уравнений не оказывает влияния на базисную единицу. А поэтому аналоги (4.13) в физике, как и в статико-динамической геометрии являются инвариантами.
Поскольку у ряда Пилецкого существует коэффициент, то использование его и золотых коэффициентов взаимосвязи обусловливает появления ряда других пропорций:
АМ ⁄АN = ВМ ⁄ ВN ; АМ ⁄АN = СД ⁄АВ ; ВМ ⁄ ВN = СД ⁄АВ ;
АМ ⁄ВМ = СД ⁄АМ ; АМ ⁄ВN = СД ⁄АN ; ВМ ⁄АN = АМ ⁄АВ ; и т.д.
Могут появляться и такие, экзотические для проективной геометрии, пропорции модулей отрезков:
|АN|2 ⁄ |ВN|2 = ВМ ⁄ АN; |ВМ|2 ⁄ |АN|2 = АМ ⁄ ВN; (4.14)
|АМ|3⁄ |ВМ|3 = ВМ ⁄ ВN; |АN|4 ⁄ |ВN|4 = АМ ⁄ ВN; и т.д.
Все пропорции модулей могут быть скомпонованы по единой форме и приравнены к базисной единице:
АМ·ВN ⁄ АN·ВМ = 1; АМ·АВ ⁄ АN·СД = 1;
|АN|3 ⁄ |ВN|2·ВМ = 1; |ВМ|2·ВN ⁄ |АN|2 ·АМ = 1; (4.15)
|АМ|3·ВN ⁄ |ВМ|4 = 1; |АN|4 ⁄ |ВN|3·АМ = 1; и т.д.
Базисная единица, стоящая в правой части каждого уравнений (4.13)–(4.15), свидетельствует, что сложные отношения множества модулей пропорционально сбалансированы. При дальнейшем движении поляры точки серий М и N тоже передвигаются, но величина каждого модуля изменяется таким образом, что их пропорциональность базисной единице сохраняется. Эта сбалансированность сохраняется и в том случае, когда отношения модулей приравниваются друг другу через их равенство базисной единице:
АМ·ВN ⁄ АN·ВМ = АМ·АВ ⁄ АN·СД;
|АN|3 ⁄ |ВN|2·ВМ = |ВМ|2·ВN ⁄ |АN|2 ·АМ; (4.16)
|АМ|3·ВN ⁄ |ВМ|4 = |АN|4 ⁄ |ВN|3·АМ;
Пропорции типа (4.16) можно подвергнуть дальнейшим преобразованиям и приравнивать базисной единице:
АМ·ВN·АN·СД ⁄ АN·ВМ·АМ·АВ = 1;
Дата добавления: 2021-02-10; просмотров: 111; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
