Дифференциальное исчисление функций одной переменной.
6.1. Понятие производной и её свойства
1) Определение производной функции в точке, односторонние
производные, несобственные производные. Примеры вычисления
производных с использованием только определения производной.
Необходимое и достаточное условие существования производной в точке
(связь производной с односторонними производными).
2) Геометрическая и физическая (механическая) интерпретация
производной.
3) Формула Вейерштрасса (с выводом). Связь формулы с
дифференцируемостью функции в точке (3-я теорема Вейерштрасса).
4) Соотношение между непрерывностью и дифференцируемостью
функции в точке (теорема с доказательством).
5) Общие правила вычисления производных : производная постоянной (с
выводом), производная линейной комбинации функций ( с выводом),
производная произведения (в частности, производная степенной
функции), производная частного (в частности, производная
отрицательной степени), производные сложной и обратной функций.
Примеры применения правил дифферренцирования.
6) Дифференциал функции в точке : определение, обозначения,
геометрический смысл, применение в приближённых вычислениях.
Примеры применения в приближённых вычислениях.
7) Производные и дифференциалы высших порядков : определения и
|
|
|
примеры вычисления.
6.2. Приложения производной
1) Теоремы о среднем в дифференциальном исчислении : теоремы Ролля,
Лагранжа, Коши.
2) Производная и монотонное поведение функций : нахождение участков
возрастания и убывания функции.
3) Экстремумы функций : локальные и глобальные экстремумы,
необходимое условие экстремума, стационарные точки; точки,
"подозрительные" на наличие экстремума. Правило определения вида
экстремума (максимум, минимум, отсутствие экстремума).
4) Выпуклые и вогнутые функции : определения, геометрическая
интерпретация, достаточное условие выпуклости (вогнутости), точки
перегиба графика и их нахождение.
5) Примерная схема исследования функции.
6) Формула Тейлора. Остаточный член формулы Тейлора. Представление
основных элементарных функций по формуле Тейлора. Вычислительные
приложения формулы.
Комплексные числа.
1) Понятие комплексных чисел, геометрическое изображение комплексных чисел.
2) Формы записи комплексных чисел.
3) Действия над комплексными числами ( сложение, вычитание, умножение, деление, извлечение корней из комплексных чисел).
8. Интегральное исчисление функций одной переменной:
|
|
|
8.1. Определённый интеграл
1) Понятие криволинейной трапеции. Вычисление площади криволинейной
трапеции в простейших случаях : f(x)=const, f(x) - кусочно-линейная функ-
ция.
2) Вычисление площади криволинейной трапеции в случае непрерывной
функции (с помощью верхних и нижних сумм функции на отрезке).
3) Разбиение отрезка, последовательность разбиений, допустимая
последовательность разбиений. Допустимость равномерной
последовательности разбиений.
4) Интегральная сумма функции, соответствующая заданному разбиению
отрезка, и её геометрическая интерпретация. Последовательность интег-
ральных сумм.
5) Определение определённого интеграла, обозначения, терминология. Гео-
метрическая интерпретация определённого интеграла.
6) Понятие функции, интегрируемой на отрезке. Примеры классов
интегрируемых функций.
7) Свойства определённого интеграла.
8.2. Неопределённый интеграл
1) Определённый интеграл как функция верхнего предела и его свойства.
2) Определение первообразной функции. Структура множества первообраз -
ных для заданной функции. Интеграл с переменным верхним пределом как
одна из первообразных непрерывной функции.
3) Определение неопределённого интеграла как совокупности
|
|
|
первообразных для заданной функции.
4) Формула Ньютона-Лейбница вычисления определённого интеграла
(теорема с доказательством). Примеры применения формулы.
5) Взаимная обратимость операций интегрирования и дифференцирования.
6) Простейшие методы интегрирования : метод замены переменной и метод
интегрирования по частям.
8.3. Несобственные интегралы
1) Несобственные интегралы 1-типа : определение, вычисление, примеры.
2) Несобственные интегралы 2-типа : определение, вычисление, примеры
9. Функции многих переменных : основные понятия
1) Определение функции двух и более переменных,область определения,
множество значений функции, графическое изображение функций двух
переменных.
2) Понятие о линейном пространстве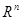 
. Окрестность точки в пространстве
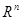. Предел последовательности точек в 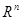и предел функции n перемен -
ных в точке. Свойства операции предельного перехода для функций мно-
гих переменных.
3) Непрерывность функций многих переменных. Свойства непрерывных
функций.
4) Понятие о частных производных 1-го порядка для функций многих пере-
менных. Вычисление частных производных 1-го порядка. Понятие полной
производной. Частные производные 2-го и более высоких порядков, их вы-
числение.
5) Дифференцируемость функции двух переменных в точке. Достаточное
|
|
|
условие дифференцируемости. Понятие о полном дифференциале
функции двух переменных в заданной точке, его применение для
приближённых вычислений. Полный дифференциал функции n
переменных и его представление с помощью скалярного произведения.
6) Локальные и абсолютные экстремумы функций многих переменных
Необходимое условие экстремума.
10. Дифференциальные уравнения
1) Понятие обыкновенного дифференциального уравнения порядка n.
Примеры обыкновенных дифференциальных уравнений разных порядков.
2) Понятие решения дифференциального уравнения. Общее и частное реше-
ния. Начальные условия для дифференциального уравнения порядка n.
Примеры начальных условий. Геометрическая интерпретация общего и
частного решений.
3) Дифференциальные уравнения 1-го порядка :
а) Метод разделения переменных - общее описание.
4) Линейные дифференциальные уравнения :
а) Понятие линейного дифференциального уравнения порядка n. Однород-
ные и неоднородные уравнения.
б) Нахождение общего решения однородного линейного дифференциаль-
ного уравнения 1-го порядка :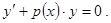 
в) Нахождение частного решения неоднородного линейного дифференци-
ального уравнения 1-го порядка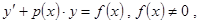 
методом
вариации произвольной постоянной. Общее решение неоднородного ли-
нейного дифференциального уравнения 1-го порядка.
г) Однородные линейные дифференциальные уравнения 2-го порядка с по-
стоянными коэффициентами :
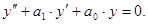
д) Однородные линейные дифференциальные уравнения порядка n с пос-
тоянными коэффициентами :
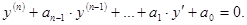
е) Решение неоднородных линейных дифференциальных уравнений с пос-
тоянными коэффициентами :
.
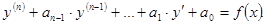11. Числовые и степенные ряды
1) Общие сведения о числовых рядах : определение, общий член ряда,
частичные суммы, сходимость и расходимость ряда.
2) Свойства сходящихся рядов. Необходимое условие сходимости ряда.
3) Ряды с неотрицательными членами : понятие и признаки сходимости
( сравнение рядов, признак 
, интегральный признак ).
4) Знакочередующиеся ряды. Признак Лейбница сходимости таких рядов.
5) Абсолютная и условная сходимость рядов. Признак сходимости знако-
переменных рядов.
6) Степенные ряды : определение, сходимость в точке, область сходимости.
Теорема Абеля.
7) Радиус сходимости степенного ряда и его вычисление. Дифференцирова -
ние и интегрирование степенных рядов.
12. Элементы линейной алгебры.
12.1. Системы линейных уравнений
1) Система двух линейных уравнений с двумя неизвестными и её геометри -
ческая интерпретация. Решение системы с помощью определителей.
2) Система двух линейных уравнений с тремя неизвестными и её геометри -
ческая интерпретация. Множество решений системы и его описание.
3) Общий вид системы m линейных уравнений с n неизвестными. Однород -
ные и неоднородные системы уравнений. Понятие решения и множества
решений системы.
4) Метод Гаусса решения системы линейных уравнений.
Дата добавления: 2020-12-12; просмотров: 74; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!