Эти два условия называются аналитическими условиями равновесия для плоской системы сходящихся сил.

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Теорема о трех не непараллельных силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

Так как F1 + F2 + F3 = 0, то F1 + F2 = R12 = - F3. Cледовательно, согласно аксиоме 1 линия действия силы F3 пересекает точку О - сходимости сил F1 и F2.

В трёхмерном пространстве сходящаяся система сил является статически определимой, если число неизвестных сил в ней не превышает трёх.

5. Сложение параллельных сил.

Найдем равнодействующую двух действующих на твердое тело параллельных сил в двух случаях:

1. Силы направлены в одну сторону.

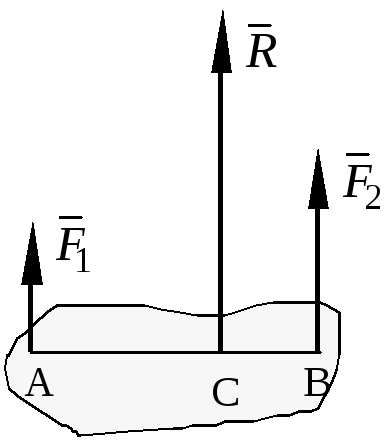
Равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону, равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в туже сторону. Линия действия равнодействующей проходит между точками приложения слагаемых сил на расстояниях от этих точек, обратно пропорциональных этим силам.

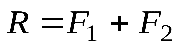
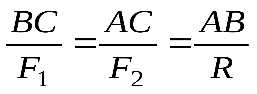, . (1.15)

2. Силы направлены в разные стороны.

Р 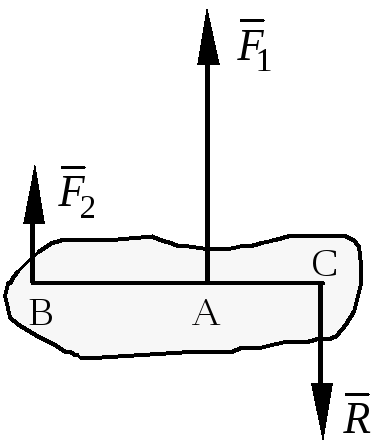авнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в разные стороны, равна по модулю разности модулей слагаемых сил, им параллельна и направлена в сторону большей силы. Линия действия равнодействующей проходит вне отрезка, соединяющего точки приложения слагаемых сил, на расстояниях от этих точек, обратно пропорциональных силам.

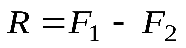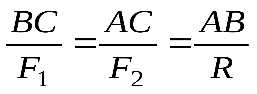, . (1.16)

С помощью приведенных формул можно решать задачи и о разложении силы на две ей параллельные.

6. Момент силы относительно точки и оси.

Момент силы относительно точки

Момент силы- вращательное усилие, создаваемое вектором силы относительно точки.

рассмотрим случай для плоской системы, где все силы лежат в одной плоскости:

Если система состоит из сил, расположенных в одной плоскости (такая система сил называется плоской), и требуется определять их моменты относительно точек той же плоскости, то нет смысла определять их как векторы, так как все они будут направлены перпендикулярно плоскости расположения сил. Поэтому в случае плоской системы сил момент определяется как алгебраическая величина:

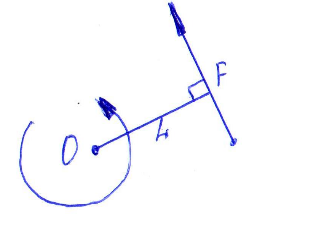
Mо=±FxL

F- сила

L- плечо измеряется Н/м (Ньютон/метр)

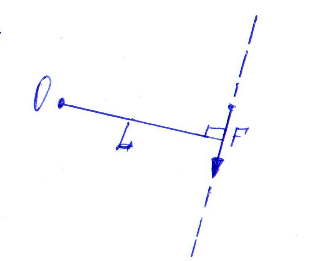
Плечом L выступает расстояние по нормали (нормаль - это мин. расстояние: линия, опущенная под углом 90градусов на линию вектора/плоскость) от рассматриваемой точки О до линии действия силы.

Увеличение силы F или ее плеча L приводят к возрастанию величины момента.

Если линия силы проходит через саму точку О, то момент силы не создается, т е равен 0

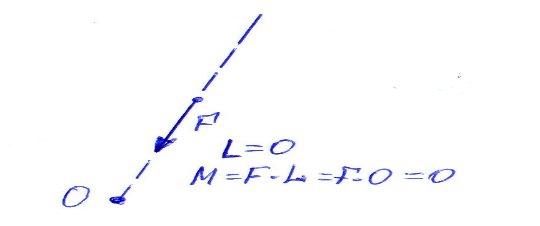
Mо=Fx0=0

Момент силы считается (+) если сила направлена против часовой стрелки

(-) если сила направлена по часовой стрелки

Mо(F1)=+ (F1)xL1 Mо (F2)= - (F2)xL2

Суммарный момент для всех сил + и -:

Σ Mо(Fn)=+(F1)xL1 +(- (F2)xL2) надо обращать внимание на знаки.

Момент силы относительно центра (точки) как векторное произведение.

Введенного понятия "момент силы относительно центра как алгебраическая величина" оказывается недостаточно в случае сил, произвольно расположенных в пространстве. Плоскости поворота у разных сил будут различными и должны задаваться дополнительно.

Удобно ввести понятие "момент силы относительно центра как в е к т о р", модуль которого равен произведению модуля силы на ее плечо, а направление перпендикулярно плоскости, проходящей через линию действия силы и центр момента.

Моментом относительно точки называется векторное произведение радиус-вектора точки приложения силы на вектор силы.

Иначе говоря, вектор 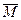o( 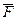) может быть определен векторным произведением:

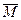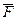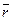o( )= x 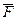, (1.2)

где r – радиус-вектор точки приложения силы относительно точки О (рис.)

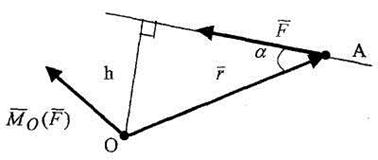
Модуль момента, согласно правилу векторного произведения, равен

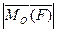= Fr sin 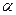= Fh, (1.3)

где 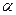– угол между векторам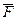и и 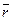; h – плечо силы 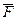относительно центра О.

Момент силы относительно оси

Момент силы относительно оси, например Oz (рисунок 1.18), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси (F’) относительно точки пересечения оси с плоскостью, т.е.

Mz(F) = MO(F’) = F’∙ h’. (1.9)

Момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.

Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например Mz(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, Mz(Q).

Момент силы относительно оси – скалярная величина.

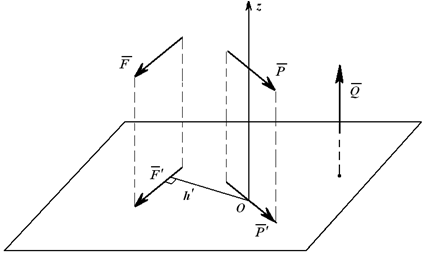
Рисунок 1.18

Моменты силы относительно координатных осей можно получить, расписав векторное произведение

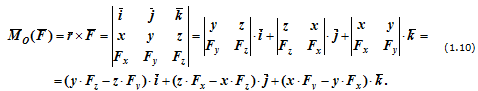
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.

7. Пара сил. Свойства пары.

Пара сил - это система двух равных по модулю, параллельных и направленных в противоположные стороны сил.

Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.

Расстояние между линиями действия сил пары называется плечом пары.

П 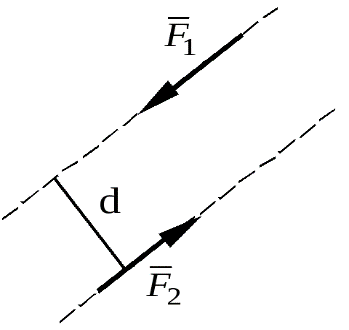ара сил не имеет равнодействующей. Действие пары на тело сводится к некоторому вращательному эффекту, численно характеризуемому моментом пары сил.

Моментом пары сил называется величина, равная взятому с соответствующим знаком произведению модуля одной из силы пары на ее плечо

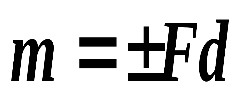. (1.17)

Свойства пары сил

1. Действие пары сил на тело не изменится, если у нее произвольным образом изменить силы и плечо при неизменном моменте пары.

2. Не изменяя действия пары сил, ее можно переносить произвольным образом в плоскости ее действия.

3. Пару сил можно повернуть в плоскости ее действия на любой угол.

4. Действие нескольких пар сил, приложенных в одной плоскости, можно заменить одной парой сил, момент которой равен алгебраической сумме моментов заданных пар сил.

8. Равновесие системы пары сил

Система пар сил, приложенных к ТТ (твердому телу), будет уравновешена, если момент результирующей пары равен нулю.

Таким образом, из соотношений системы пар следуют:
условия равновесия системы пар сил:

1.Необходимым и достаточным условием равновесия системы пар в пространстве является равенство нулю геометрической суммы вектор-моментов слагаемых пар:

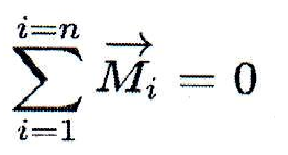
Условие 1 имеет геометрическую интерпретацию и означает замкнутость многоугольника, образованного из векторов моментов пар.

2.Необходимым и достаточным условием равновесия системы пар на плоскости является равенство нулю алгебраической суммы моментов слагаемых пар:

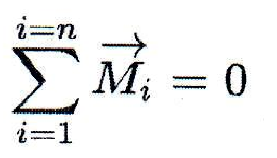
9. Теорема о трех силах.

Теорема. Если твердое тело находится в равновесии под действием трех сил, и линии действия двух сил пересекаются, то линия действия третьей силы проходит через точку пересечения первых двух, и все три силы лежат в одной плоскости.

Доказательство:

Пусть тело находится в равновесии под действием трех сил 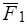, 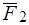и 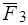, причем линии действия 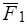и 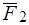пересекаются в точке 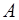(рис. 16а).

Согласно следствию 1 из аксиом статики, силы 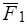и 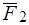можно, не нарушая состояние равновесия тела, перенести вдоль их линий действия в точку 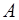(рис. 16б), а затем по аксиоме 3 заменить одной силой 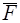( рис. 16в), проходящей через точку пересечения сил 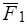и 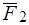(точку 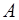) и лежащей с ними в одной плоскости, причем 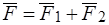. Тело находится в равновесии под действием двух сил 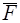и 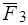( рис. 16в), следовательно, по аксиоме 1 они должны иметь общую линию действия, но тогда силы 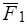, 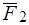и 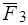лежат в одной плоскости и их линии действия пересекаются в одной точке (точку ).

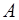10. Лемма о параллельном переносе силы.

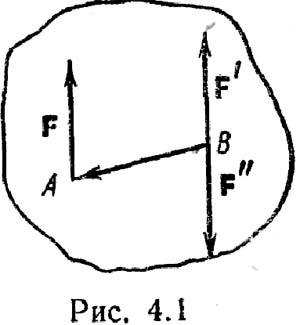
Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F~(F, F', F"), так как (F',F")~0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=M_B(F). Таким образом, лемма о параллельном переносе силы доказана.

11. Приведение произвольной системы сил к простейшему виду. Главный вектор и главный момент системы сил.

Основная теорема статики. Произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору системы сил и приложена в произвольно выбранной точке тела (центре приведения), момент пары равен главному моменту системы сил относительно этой точки.

M_O = M_O(F₁) + M_O(F₂) + ... + M_O(F_n) = 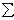M_O(F_i)– главный момент

R = F₁ + F₂ + ... + F_n = 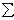F_i– главный вектор

В этом случае система сил 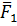, , 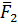, 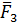… , 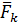заменяется одной силой 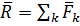и суммой моментов, а именно произведений каждой из этих сил на расстояние от точки её приложения до некоторого центра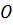

Интересные замечания.

1. Сила 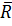не является здесь равнодействующей, так как заменяет систему сил не одна, а с появившейся парой сил, имеющей момент .

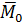2. Значение 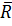от выбора центра 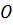не зависит, а значение 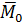меняется с изменением центра 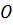, в который переносятся силы.

3.Результат приведения зависит от значений и направлений главного вектора 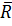и главного момента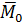

ПРИМЕР (для себя)

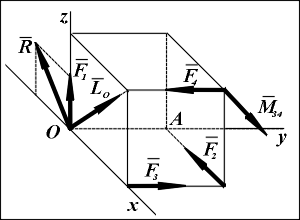
К вершинам куба с длиной ребра a приложена система четырех сил, действующих вдоль ребер куба и имеющих одинаковые модули: F1 = F2 = F3 = F4 = F.

Определить главный вектор этой системы сил и ее главный момент относительно вершины О.

Решение. Введем координатную систему Oxyz, оси которой ориентированы вдоль ребер куба.

Силы F3, F4 образуют пару сил с векторным моментом M34, направленным в положительном направлении оси Ox (точка приложения вектора M34 может быть выбрана произвольно) и равным по модулю M34 = F · a. Следовательно, силы F3 и F4 можно не учитывать при вычислении проекций главного вектора R.

Определяем проекции главного вектора R:

Rх = F1x + F2x = 0 - F2 = -F;

Ry = F1y + F2y = 0;

Rz = F1z + F2z = F + 0 = F.

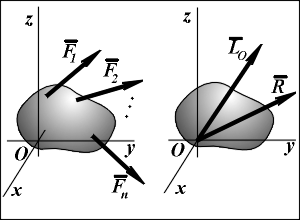
Модуль R = (Rх + Ry + Rz) 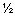= 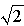· F.

Вычисляем проекции главного момента LO относительно точки О, определяя осевые моменты сил F1 и F2 геометрическим методом (напомним, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости) и проецируя векторный момент M34 на оси координат:

LOx = MOx(F1) + MOx(F2) + (M34)x = 0 + 0 + M34 = F a;

LOy = MOy(F1) + MOy(F2) + (M34)y = 0 + 0 + 0 = 0;

LOz = MOz(F1) + MOz(F2) + (M34)z = 0 + F · OA + 0 = F a;

Модуль LO = (LOх + LOy + LOz) 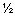= 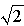· F · a.

Таким образом, для заданной системы сил ее главный вектор R и главный момент LO относительно точки О равены по модулю R = 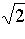· F; LO= 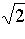· F · a, лежат в плоскости Oxz и образуют с осью Oz углы в 45° (см. рис.).

12. Условия равновесия произвольной системы сил.

Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.

Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).

Дата добавления: 2020-04-08; просмотров: 239; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!